Задачи по теории множеств. Задачи по теории множеств Задание 1

• Название: Задачи по теории множеств Задание 1
• Дата: 13.10.2021
• Размер: 86.9 Kb.
• Имя файла: Задачи по теории множеств.docx
• Тип: Документы; #246620

Задачи по теории множеств

Задание 1.

Запишите с помощью математических символов следующие предложения:

• 
  4 натуральное число;
  
• 
  2,1 не является целым числом;
  
• 
  множество В является подмножеством множества О;
  
• 
  множества К и С равны;
  

Задание 2.

Задайте множества А и В другим способом, если А ={1, 2, 3, 4, 5, 6, 7,8}, В = {b, b  N, b6}. Изобразите эти множества с помощью кругов Эйлера, каково отношение между этими множествами?

Задание 3.

Р – множество натуральных чисел, больших 7 и меньших 14. Выясните, какие из чисел 13, 10, 5, 7, 14 ему принадлежат, а какие не принадлежат. Запишите решение, используя математические символы.

Задание 4.

А – множество решений уравнения  . Верно ли, что А – пустое множество? Приведите примеры уравнений, множество решений которых состоит из:

• 
  одного элемента;
  
• 
  двух элементов;
  
• 
  трех элементов.
  

Задание 5.

Запишите множество букв в слове «математика» и множество цифр в записи числа 515353.

Задание 6.

Изобразите на координатной прямой множество Х, если: 

• 
  
  
• 
  
  
• 
  .
  

Задание 7.

Задайте двумя способами множество точек координатной прямой (рис.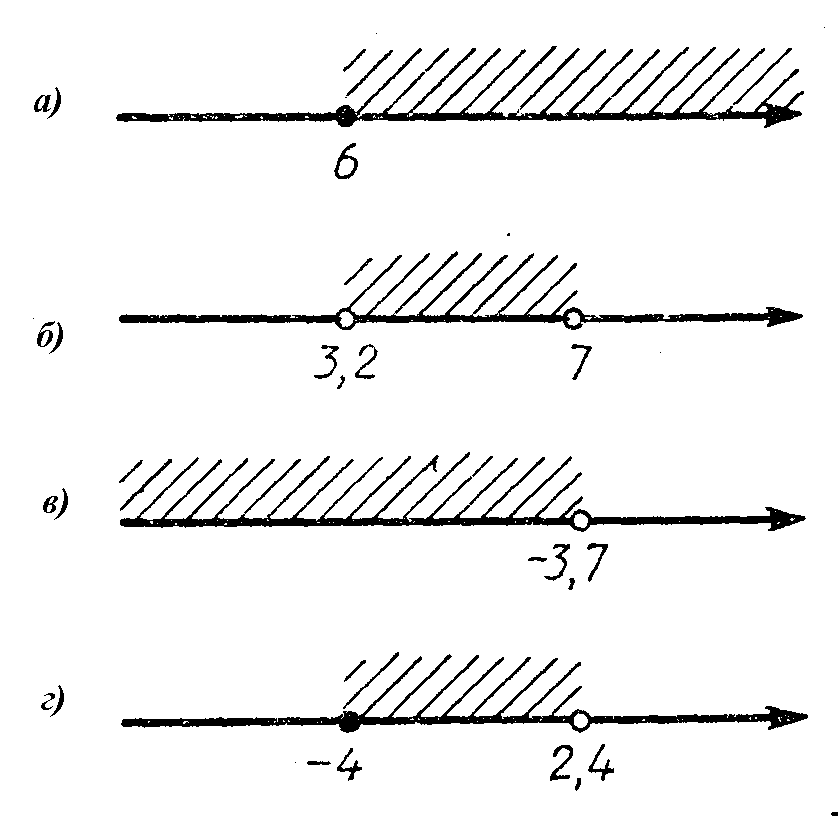



Задание 8.

Постройте прямую и отметьте на ней начало отсчета, единичный отрезок, точку А(5) и все точки, расстояние от которых от точки А: равно 2, не более 2.

Задание 9.

Дано множество С = {213, 45, 324, 732, 136}. Составьте подмножества множества С, состоящие из чисел, которые: 

• 
  делятся на 3; 
  
• 
  не делятся на 4; 
  
• 
  не делятся на 5.
  

Задание 10.

А – множество натуральных чисел, меньших 20; В, С, Е, Н – подмножества множества А, такие, что В состоит из чисел, кратных 6, С – из чисел, кратных 2, Е – из чисел, кратных 3, Н – из чисел, кратных 2 и 3 одновременно. Перечислите элементы множеств А, В, С, Е, Н и укажите среди них равные множества.

Задание 11.

Пусть разные строчные буквы обозначают разные предметы. Для каких из следующих пар множеств имеет место отношение А В или В  А:

• 
  А={а, b, с, d}, В = {а, с, d}; 
  
• 
  А = {а, b}, В = {а, с, d}; 
  
• 
  А =, В = ;
  
• 
  А =, В = {а, b, с}.
  

Задание 12.

Равны ли следующие множества: А = {2, 4, 6} и В = {6, 4, 2}; А = {1, 2, 3} и В ={I, II, III}; А = {{1, 2} {2, 3}} и В = {2, 3, 1};