Задача по финансовой математике. Финматематика. Задана матрица последствий

• Название: Задана матрица последствий
• Анкор: Задача по финансовой математике
• Дата: 19.01.2022
• Размер: 47.05 Kb.
• Имя файла: Финматематика.docx
• Тип: Документы; #335671

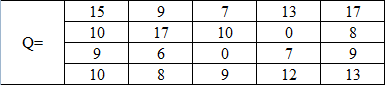
Задана матрица последствий Q. Найдите матрицу рисков. Проведите анализ ситуации полной неопределенности, применив правила по принятию решений Вальда, Сэвиджа и Гурвица (взять λравному 0,4; 0,45и 0,3). Проведите анализ ситуации частичной неопределенности при известных вероятностях того, что реальная ситуация развивается по варианту j: 0,1; 0,3; 0,1; 0,15; 0,35 (примените правила максимизации среднего ожидаемого дохода и минимизации среднего ожидаемого риска)

Задана матрица последствий

Из каждого столбца найдём Qmax. После этого из Qmax отнимаем все значения столбцов и получаем матрицу рисков R .Результаты представлены на рисунке.

Рис.4 –Матрица доходности и матрица последствий.

Теперь проведём анализ ситуации полной неопределенности, применив правила по принятию решений Вальда, Сэвиджа и Гурвица.

Начнем с критерия Вальда .Вернемся к матрице последствий и из каждой строки выберем наименьшее значение.Результаты представлены на рисунке

Рис.5-Критерий Вальда

Теперь найдём из представленных решений максимальное значение. Из рисунка видно , что по критерию Вальда рекомендуют принять 4 решение.

Теперь рассмотрим какое решение рекомендует критерий Сэвиджа. Рассмотрим матрицу рисков и из каждой строки выберем наибольшее значение. Результаты представлены на рисунке.

Рис.6-Критерий Сэвиджа

Из данных значений выберем минимальное . По критерию Сэвиджа оптимальным решением является 1 , которому соответствует наименьшее число 8.

Рассмотрим критерий Гурвица.Формула критерия Гурвица: K= λmax(qi)+(1- λ)min(qi). Расчеты представлены на рисунке

Таблица 2,3,4- Вспомогательные таблицы для критерия Гурвица

кр. Вальда				кр. Гурвица
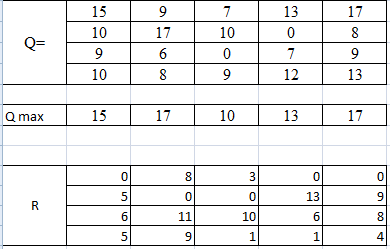
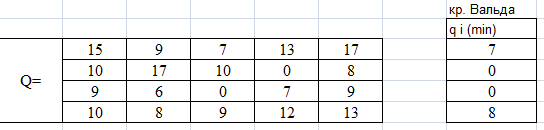
q i (min)		Q i (max)		λ =	0,4	0,45	0,3
7		17		G 1 =	13	12,5	14
0		17		G 2 =	10,2	9,35	11,9
0		9		G 3 =	5,4	4,95	6,3
8		13		G4=	11	10,75	11,5

Принимается решение i, при котором достигается максимум

Выбирая максимальное значение равное 13, приходим к выводу, что правило Гурвица рекомендует первое решение.

Выбирая максимальное значение равное 12,5, приходим к выводу, что правило Гурвица рекомендует первое решение.

Выбирая максимальное значение равное 14, приходим к выводу, что правило Гурвица и в этом случае рекомендует первое решение.

Вывод: два правила , правило Сэвиджа и Гурвица (а правило Гурвица при всех трех значениях ) рекомендуют первое решение, так что его и принимаем.

Проведём анализ ситуации частичной неопределенности при известных вероятностях того, что реальная ситуация развивается по варианту j: 0,1; 0,3; 0,1; 0,15; 0,35

Для правила максимизации средней ожидаемой доходности нам необходима матрица последствий.

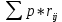Расчет будем производить по формуле Qcp= . Выбирается тот вариант решения , в котором достигается максимальное значение .Получаем :

р=	0,10	0,30	0,10	0,15	0,35
							Q i cp
Q=	15	9	7	13	17		12,8
	10	17	10	0	8		9,9
	9	6	0	7	9		6,9
	10	8	9	12	13		10,65

Максимальный средний ожидаемый доход равен 12,8 и сооответсвует 1 решению.

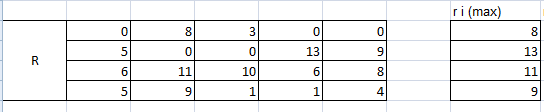
Для правила минимизации среднего ожидаемого риска нам понадобится матрица рисков. Расчет будем производить по формуле Rcp=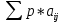 . Получаем

р=	0,10	0,30	0,10	0,15	0,35
							R i cp
R	0	8	3	0	0		2,7
	5	0	0	13	9		5,6
	6	11	10	6	8		8,6
	5	9	1	1	4		4,85

Правило рекомендует принять решение ,влекущее минимальный средний ожидаемый риск .Следовательно ,минимальный средний ожидаемый рискравен 2,7 и соответсвует 1 решению.