Курсовая работа постоянный и переменный токи. Аллочка (1). Задание Анализ линейной электрической цепи постоянного тока в установившемся режиме

• Название: Задание Анализ линейной электрической цепи постоянного тока в установившемся режиме
• Анкор: Курсовая работа постоянный и переменный токи
• Дата: 26.05.2022
• Размер: 0.53 Mb.
• Имя файла: Аллочка (1).docx
• Тип: Закон; #550374

Задание № 1. Анализ линейной электрической цепи постоянного тока в установившемся режиме

1) составить систему уравнений по законам Кирхгофа в матричной форме и определить все неизвестные токи в ветвях.

2) Составить баланс мощности для заданной схемы.

3) Определить токи в ветвях методом узловых потенциалов и сравнить их со значениями, полученными в п. 1.

4) Определить токи в ветвях заданной схемы методом контурных токов. Найденные значения токов сравнить с полученными в п. 1.

5) Определить ток в сопротивлении R4 с помощью эквивалентных преобразований и сравнить полученное значение с найденным в п. 1.

6) Построить в масштабе потенциальную диаграмму для внешнего контура.

7) Исследовать заданную электрическую цепь с помощью моделирующей программы Electronics Workbench. Измерить значения токов в ветвях и сравнить их со значениями, рассчитанными в пункте 1.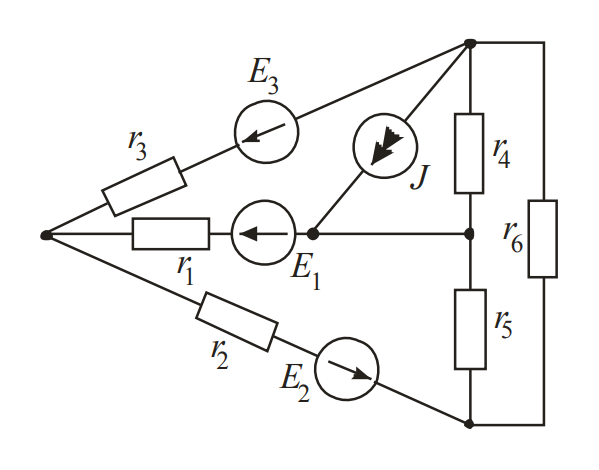



Рисунок 1 – Исходная схема

E1=5B; E2=16 B; E3=30B; J=0,4 A; r1=6 Ом; r2=4 Ом; r3=3 Ом; r4=2 Ом;

r5=5 Ом; r6= 3 Ом.

1. Зададимся направлениями токов и составим системы уравнений по законам Кирхгофа.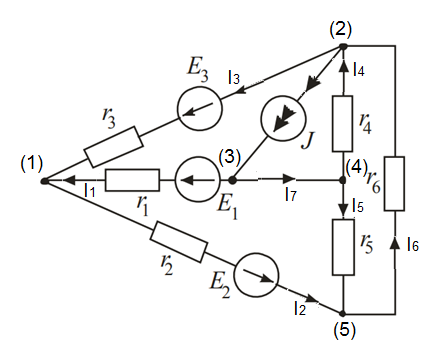



Рисунок 2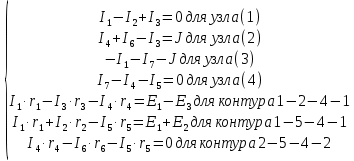



Подставим числовые значения и решим систему уравнений в MathCAD.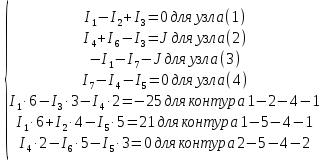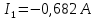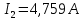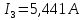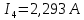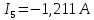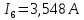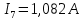



















2) Составить баланс мощности для заданной схемы.

Рассчитаем мощность потребителя: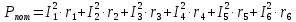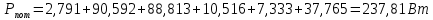





Определим мощность источников:

Для расчета мощности источников определим напряжение на источнике тока: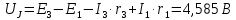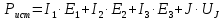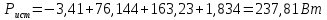







Баланс мощностей выполняется.

3) Определить токи в ветвях методом узловых потенциалов и сравнить их со значениями, полученными в п. 1.

Примем узел (5) за нулевой потенциал 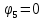. Составим систему уравнений с помощью метода узловых потенциалов:



Рисунок 3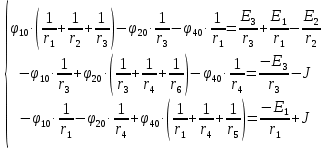



Подставим числовые значения и решим систему уравнений с помощью MathCAD.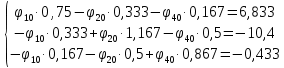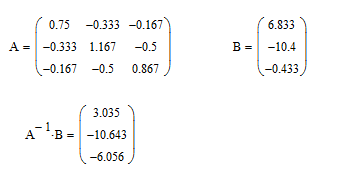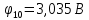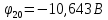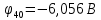











Определим токи: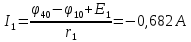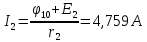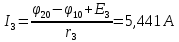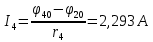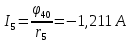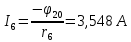















Рассчитанные токи полностью совпали с токами рассчитанные в п.1.

4) Определить токи в ветвях заданной схемы методом контурных токов. Найденные значения токов сравнить с полученными в п. 1.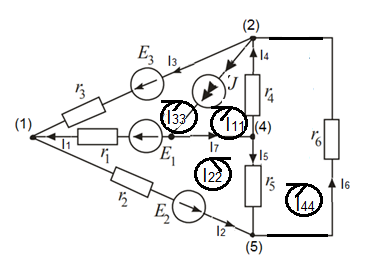



Рисунок 4

Составим систему уравнений по методу контурных токов с учетом, что I₁₁=-J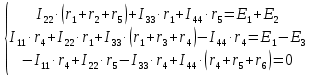



Подставим числовые значения и решим систему уравнений с помощью MathCAD.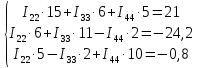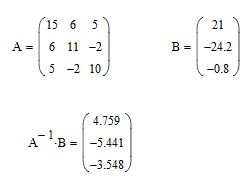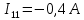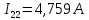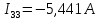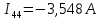













Определим токи: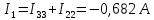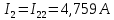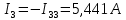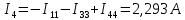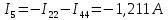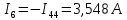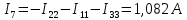















Рассчитанные токи методом контурных токов полностью совпадают с п.1

5) Определить ток в сопротивлении R4 с помощью эквивалентных преобразований и сравнить полученное значение с найденным в п. 1.

Метод эквивалентного генератора состоит в том, чтобы определить напряжение холостого хода U_xxab, следующим шагом необходимо определить эквивалентное сопротивление относительно зажимов ab, следовательно ток I₄ будет равен: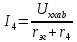



На рисунке 5 представлена схема для нахождения .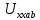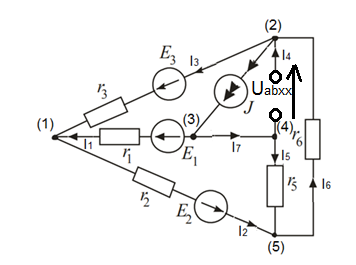



Рисунок 5 –Схема для определения напряжения холостого хода

Воспользуемся методом узловых потенциалов используемых в пункте 3, исключим из уравнения r4 и определим напряжения холостого хода.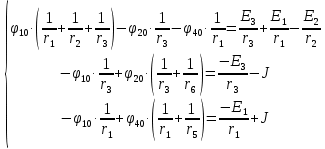



Подставим числовые значения и решим систему уравнений с помощью MathCAD.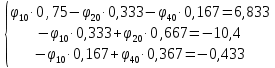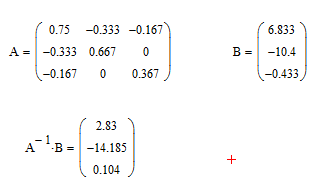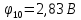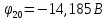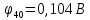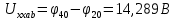













Определим входное сопротивление относительно зажимов ab, для этого закоротим все источники ЭДС и разорвем источник тока, схема представлена на рисунке 6.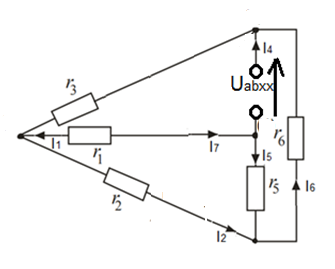



Рисунок 6 – Схема для определения эквивалентного сопротивления

Преобразуем треугольник сопротивлений r1,r2,r5 в звезду сопротивлений как показано на рисунке 7.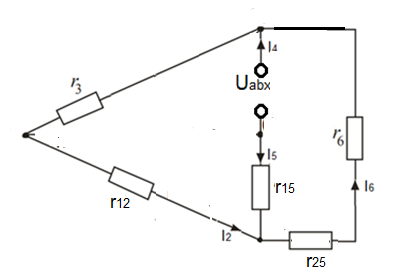



Рисунок 7 – Преобразование треугольник-звезда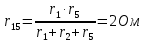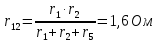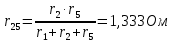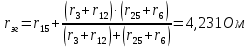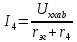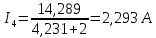













6) Построить в масштабе потенциальную диаграмму для внешнего контура.

Построим потенциальную диаграмму для внешнего контура для точек указанных на рисунке 8. Примем точку «а» за нулевой потенциал.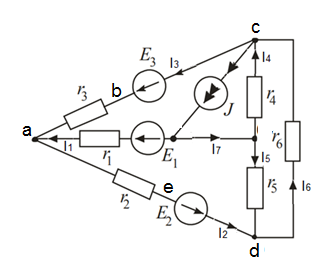



Рисунок 8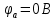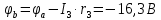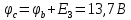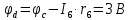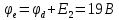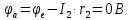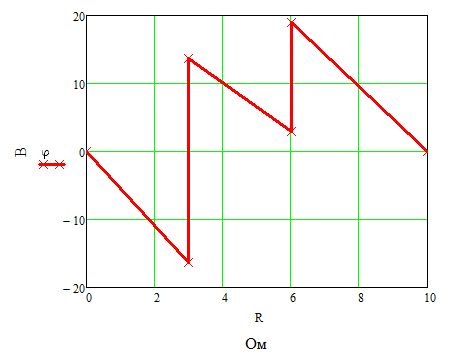















Рисунок 9 – Потенциальная диаграмма

7) Исследовать заданную электрическую цепь с помощью моделирующей программы Electronics Workbench. Измерить значения токов в ветвях и сравнить их со значениями, рассчитанными в пункте 1.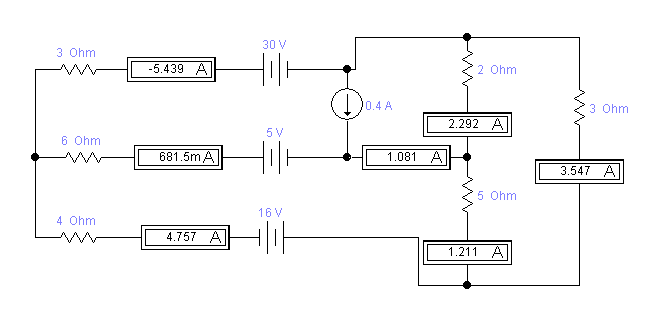



Значения токов смоделированной схемы совпадают со значениями токов в п.1

Задание № 2. Анализ линейной электрической цепи синусоидального тока в установившемся режиме

Для электрической схемы выполнить следующее:

1) Составить систему уравнений по законам Кирхгофа в дифференциальной форме.

2) Рассчитать мгновенные значения токов во всех ветвях: - по законам Кирхгофа; - методом контурных токов; - методом узловых потенциалов.

3) Составить баланс активных, реактивных, комплексов полных мощностей. 4) Построить в масштабе на одной комплексной плоскости векторную диаграмму токов и топографическую диаграмму напряжений.

5) Определить показания вольтметра и ваттметра.

6) Исследовать заданную электрическую цепь с помощью моделирующей программы Electronics Workbench. Измерить значения токов в ветвях и сравнить их с действующими значениями токов, рассчитанными в пункте 1.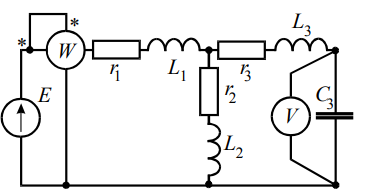



Рисунок 10 – Исходная схема

Дано:

E=120 B; f=50Гц; С₃=100 мкФ; L₁=15,9мГн; L₂=1000 мГн; L₃=115 мГн;

r₁=10 Ом; r₂=4 Ом; r₃=100 Ом.

1) Составить систему уравнений по законам Кирхгофа в дифференциальной форме.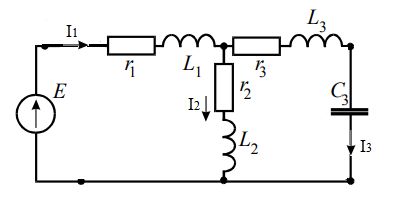



Рисунок 11

Составим систему уравнений в дифференциальной форме.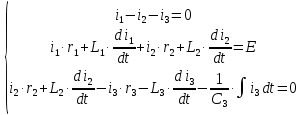



2) Рассчитать мгновенные значения токов во всех ветвях: - по законам Кирхгофа; - методом контурных токов; - методом узловых потенциалов.

Определим токи символическим методом: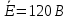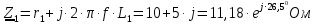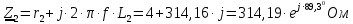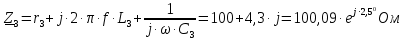









Рассчитаем токи по законам Кирхгофа: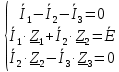



Подставим числовые значения и рассчитаем в MathCAD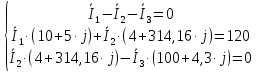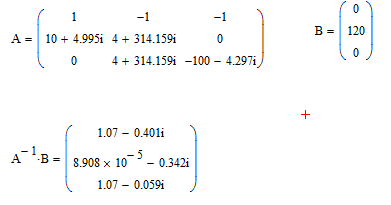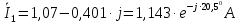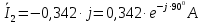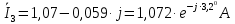











Зададимся контурными токами и рассчитаем токи в ветвях: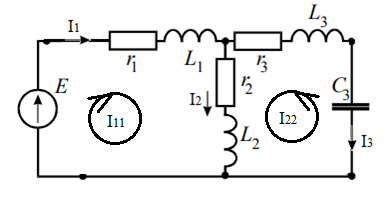



Рисунок 12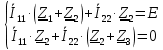



Подставим числовые значения и решим данную систему уравнений с помощью MathCAD.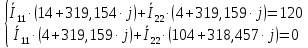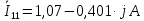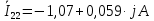









Определим токи: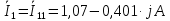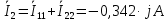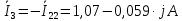







Определим токи методом двух узлов: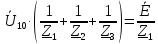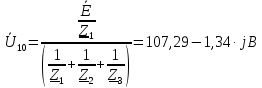





Определим токи во всех ветвях: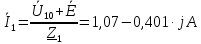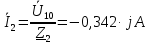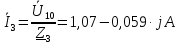







3) Составить баланс активных, реактивных, комплексов полных мощностей.

Рассчитаем активную мощность потребления: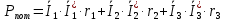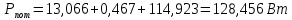





Рассчитаем реактивную мощность потребления: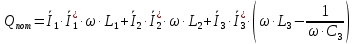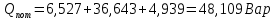





Комплексная полная мощность: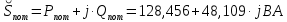



Рассчитаем активную мощность источника: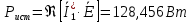



Рассчитаем реактивную мощность источника: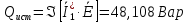



Комплексная полная мощность источника: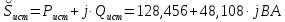



Баланс мощностей выполняется.

4) Построить в масштабе на одной комплексной плоскости векторную диаграмму токов и топографическую диаграмму напряжений.

Для построения топографической диаграммы напряжений, рассчитаем напряжения на каждом элементе: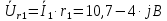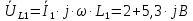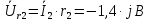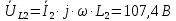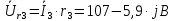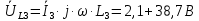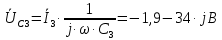















Топографическую диаграмму представим для двух контуров: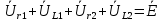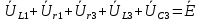





Масштаб:

1см=0,25 А; 1см= 20В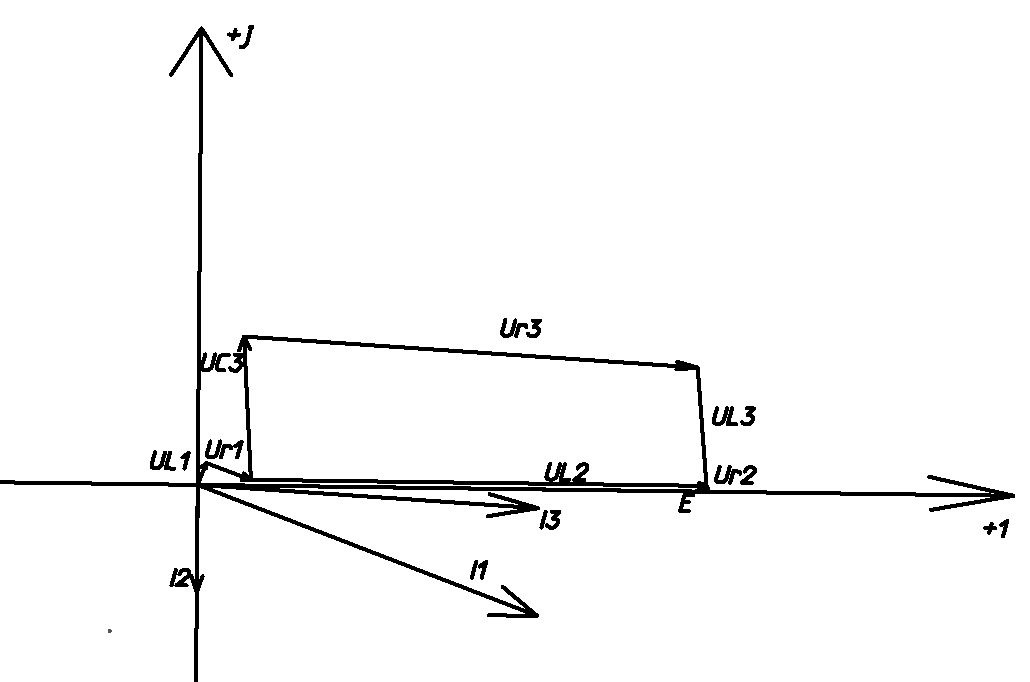



Рисунок 13 – Векторная диаграмма токов и топографическая диаграмма напряжений

5) Определить показания вольтметра и ваттметра.

Показание вольтметра это напряжение на емкости.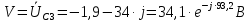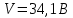





Показание ваттметра: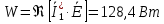



6) Исследовать заданную электрическую цепь с помощью моделирующей программы Electronics Workbench. Измерить значения токов в ветвях и сравнить их с действующими значениями токов, рассчитанными в пункте 1.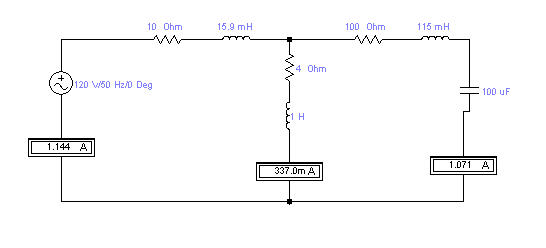



Рассчитанные действующие значения токов при моделировании совпали с рассчитанными действующими значениями токами в п.1.

Задание № 3. Анализ трехфазных цепей при различных схемах соединения нагрузки

Обмотки трехфазного генератора с симметричной системой фазных напряжений Uфг соединены звездой. Даны три схемы соединения нагрузки: звезда с нулевым проводом; звезда; треугольник.

Рассчитаем трехфазную схему с соединением нагрузки звездой с нулевым проводом:

Дано: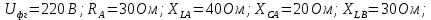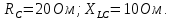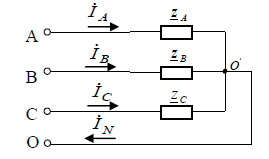







Рисунок 14 – Звезда с нулевым проводом

Рассчитаем сопротивления каждой фазы: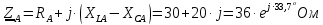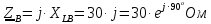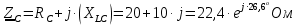







Фазные напряжения :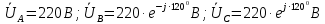



Определим линейные токи: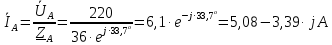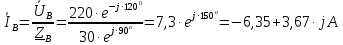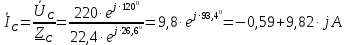







Определим ток в нейтральном проводе по первому закону Кирхгофа: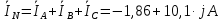



Построим векторную диаграмму токов и напряжений: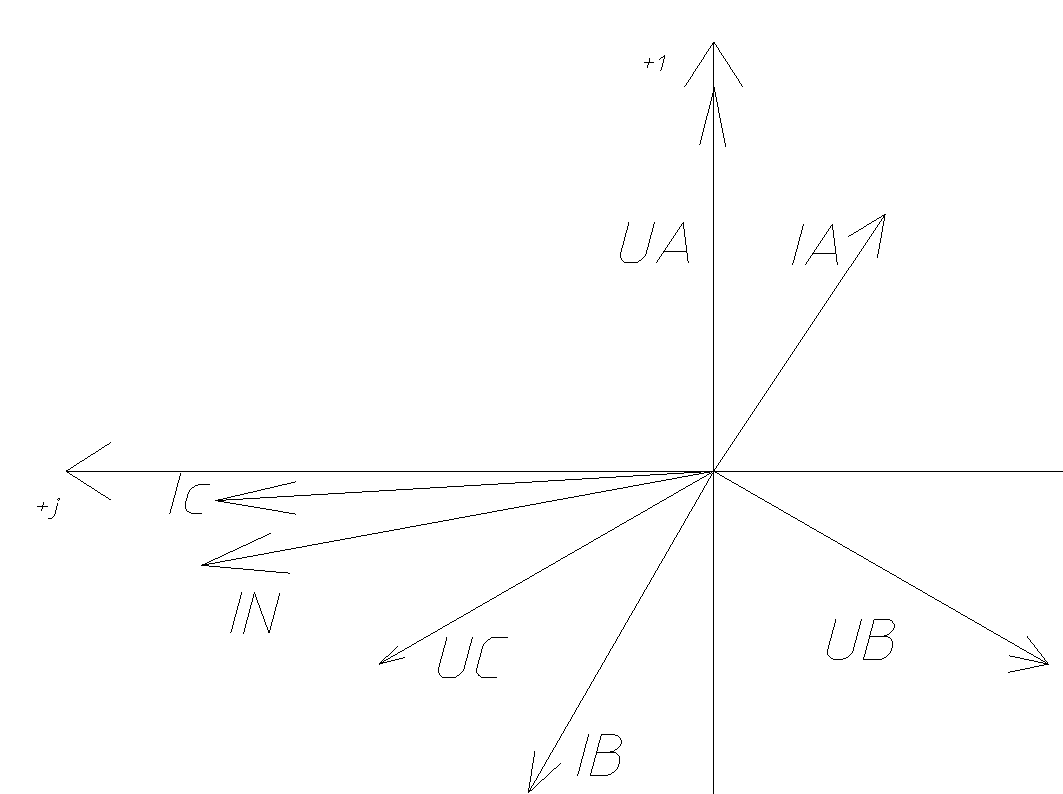



Рисунок 15 – Векторная диаграмма токов и напряжений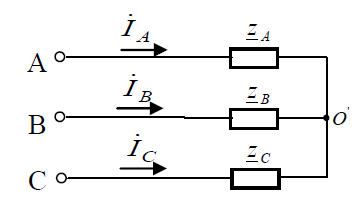



Рисунок 16 – Звезда без нулевого провода

Рассчитаем сопротивления каждой фазы: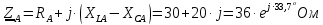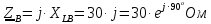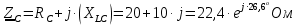







Фазные напряжения :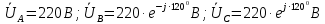



Так как отсутствует нулевой провод, то возникает перекос напряжений, рассчитаем данное напряжение: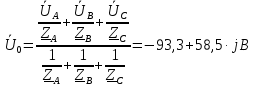



Определим напряжения на приемнике: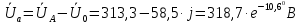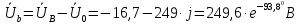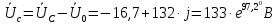







Определим линейные токи: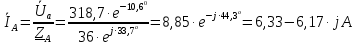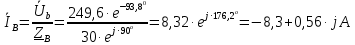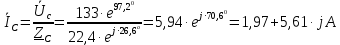







Проверка: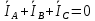



Построим векторную диаграмму токов и напряжений: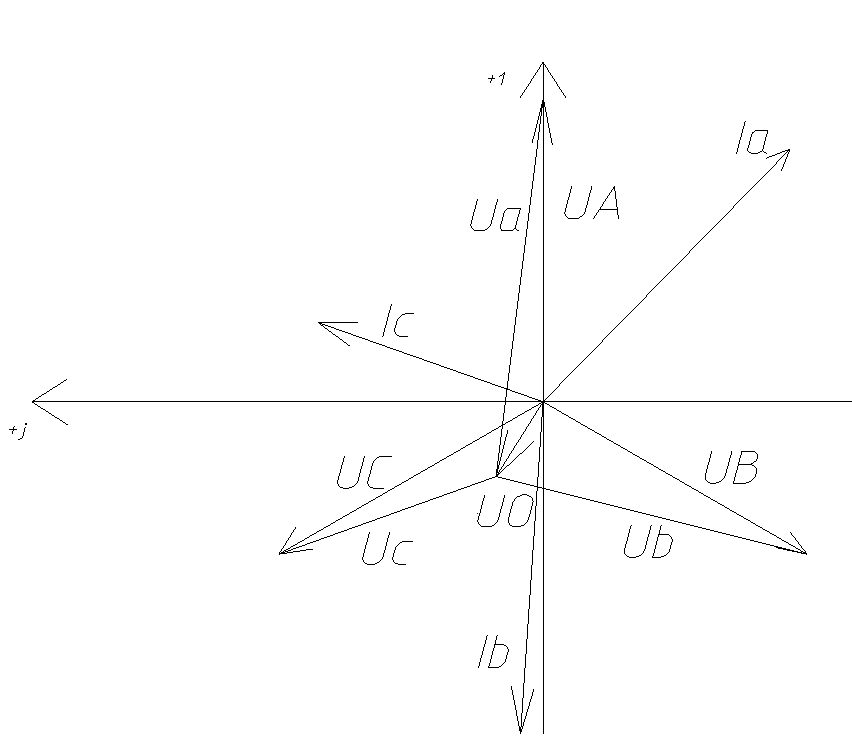



Рисунок 17 – Векторная диаграмма токов и напряжений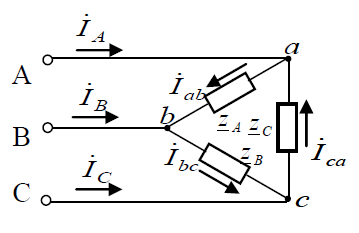



Рисунок 18 – Звезда с нулевым проводом

Рассчитаем сопротивления каждой фазы: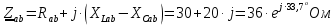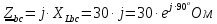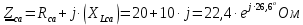







Линейные напряжения :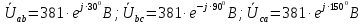



Определим фазные токи: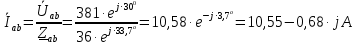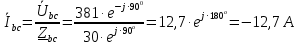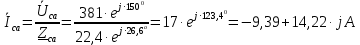







Определим линейные токи по первому закону Кирхгофа: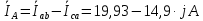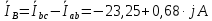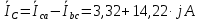







Произведем проверку: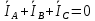



Построим векторную диаграмму токов и напряжений: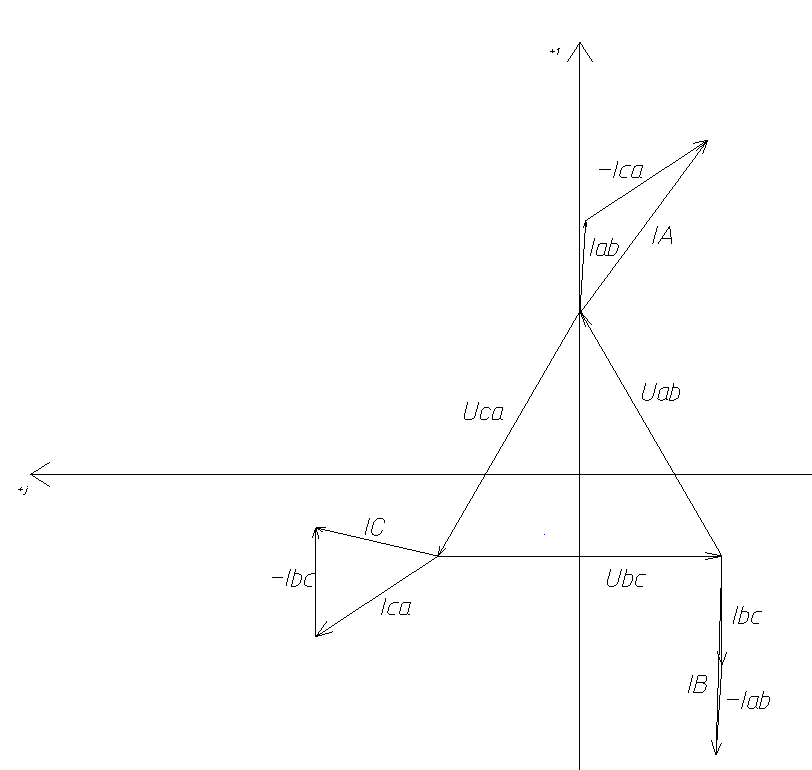



Рисунок 19 – Векторная диаграмма токов и напряжений

Задание № 4. Анализ электрической цепи с несинусоидальным источником

В линейной электрической цепи, схема и параметры которой приведены в таблицах 4.1 и 4.2, соответственно, действует источник несинусоидального напряжения. графическая форма которого задана в таблице 4.3.

Требуется:

1) представить Э Д С источника, заданную графически согласно таблице 4.3, рядом Фурье, ограничив число членов ряда четырьмя составляющими, включая постоянную составляющую, если она есть.

2) Построить графики спектров амплитуд и начальных фаз ЭДС источника.

3) После ограничения принятым количеством гармоник определить приближенное действующее значение ЭДС

4) На одном графике построить заданную кривую несинусоидальной ЭДС и кривую, полученную в результате сложения гармонических составляющих ограниченного ряда.

5) Определить токи в ветвях электрической цепи для каждой гармоники приложенного напряжения и постоянной составляющей. При расчете каждой гармоники выполнить построение векторных диаграмм токов соответствующих гармоник и проверить правильность расчётов балансом активной и реактивной мощностей.

6) Используя метод наложения, в виде ряда Фурье записать мгновенные значения токов ветвей схемы.

7) Определить действующие значения несинусоидальных токов в цепи.

8) Определить значения мощности искажения и коэффициента мощности в заданной электрической цепи.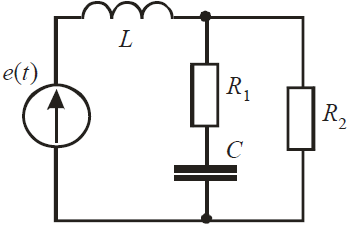



Рисунок 20 – Заданная схема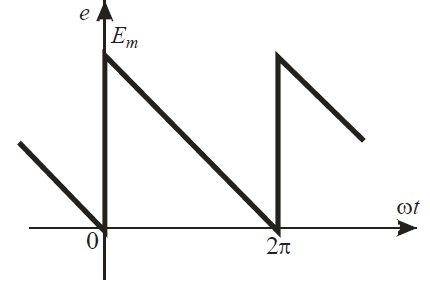



Рисунок 21 – несинусоидальное воздействие

Дано:

E_m=200 В; T=0,009 c; R1=9 Ом; R2=13 Ом; R3=9 Ом; L=10 мГн; С=55 мкФ

Определим частоту основной гармоники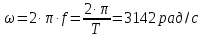

1) представить Э Д С источника, заданную графически согласно таблице 4.3, рядом Фурье, ограничив число членов ряда четырьмя составляющими, включая постоянную составляющую, если она есть.

Заданный пилообразный сигнал, воспользуемся табличным разложением данного сигнала в ряд Фурье: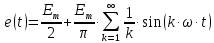



Запишем выражения ряда Фурье для постоянной составляющей и трех гармоник: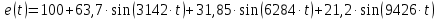



2) Построить графики спектров амплитуд и начальных фаз ЭДС источника.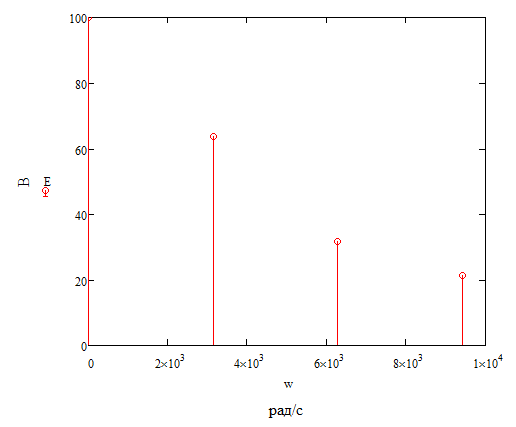



Рисунок 22 - Амплитудный спектр

Начальные фазы всех гармоник равны нулю.

3) После ограничения принятым количеством гармоник определить приближенное действующее значение ЭДС

Определим амплитудное значение ЭДС, а следом и действующее значение ЭДС.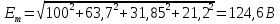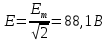





4) На одном графике построить заданную кривую несинусоидальной ЭДС и кривую, полученную в результате сложения гармонических составляющих ограниченного ряда.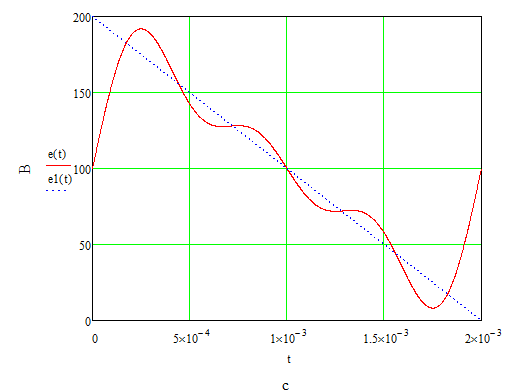



Рисунок 23 – Заданный сигнал и разложенный сигнал в ряд Фурье

5) Определить токи в ветвях электрической цепи для каждой гармоники приложенного напряжения и постоянной составляющей. При расчете каждой гармоники выполнить построение векторных диаграмм токов соответствующих гармоник и проверить правильность расчётов балансом активной и реактивной мощностей.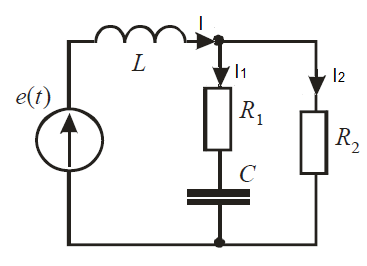



Рисунок 24

Так как на постоянном токе, сопротивление катушки индуктивности равно нулю, а конденсатора равно бесконечности, то схема принимает вид: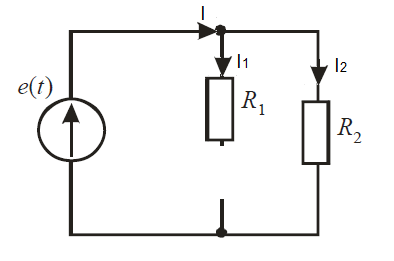



Рисунок 25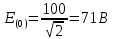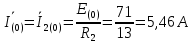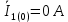







Рассчитаем баланс мощностей:

Мощность потребления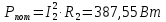



Мощность источника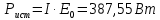



Баланс мощностей выполняется.

Рассчитаем действующие значения токов образованные от первой гармоники: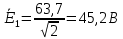



Рассчитаем сопротивления ветвей: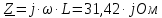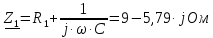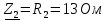







Определим сопротивление параллельного участка: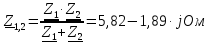



Общее сопротивление: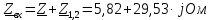



Рассчитаем токи: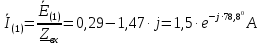



Определим напряжение на параллельном участке: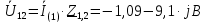



Определим токи: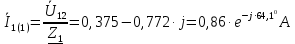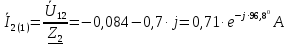





Произведем баланс мощностей: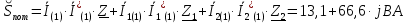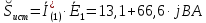





Баланс мощностей выполняется.

Рассчитаем действующие значения токов образованные от второй гармоники: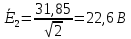



Рассчитаем сопротивления ветвей: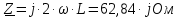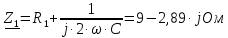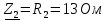







Определим сопротивление параллельного участка: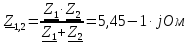



Общее сопротивление: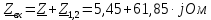



Рассчитаем токи: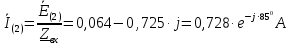



Определим напряжение на параллельном участке: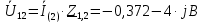



Определим токи: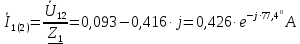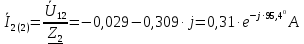





Произведем баланс мощностей: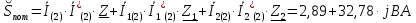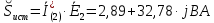





Баланс мощностей выполняется.

Рассчитаем действующие значения токов образованные от третьей гармоники: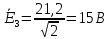



Рассчитаем сопротивления ветвей: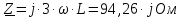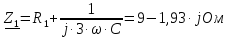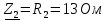







Определим сопротивление параллельного участка: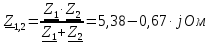



Общее сопротивление: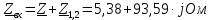



Рассчитаем токи: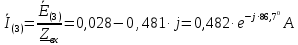



Определим напряжение на параллельном участке: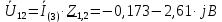



Определим токи: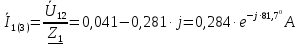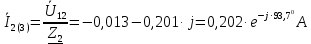





Произведем баланс мощностей: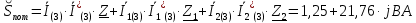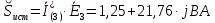





Баланс мощностей выполняется.

6) Используя метод наложения, в виде ряда Фурье записать мгновенные значения токов ветвей схемы.

Действующие значения токов переведем в амплитудные значения: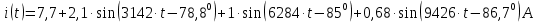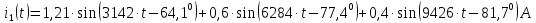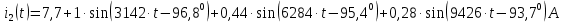







7) Определить действующие значения несинусоидальных токов в цепи.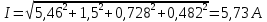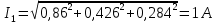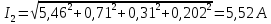







8) Определить значения мощности искажения и коэффициента мощности в заданной электрической цепи.

Мощность искажения определяется по формуле: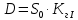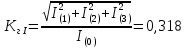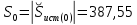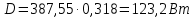









Коэффициент мощности определяется по следующей формуле: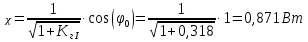