2 задачи. Задание 1. Алгоритм шифрования гост 2814789
 Скачать 16.87 Kb. Скачать 16.87 Kb.
|
|
Титульный лист Задание №1. Алгоритм шифрования ГОСТ 28147-89. Выполните первый цикл алгоритма шифрования ГОСТ 28147 89 в режиме простой замены. Для получения 64 бит исходного текста используйте 8 первых букв из своих данных: Фамилии Имени Отчества. Для получения ключа (256 бит) используют текст, состоящий из 32 букв. Первый подключ содержит первые 4 буквы. Выполнение Исходные данные для зашифрования: КРЫЛОВА Для ключа возьмем последовательность, состоящую из 32 букв: АЛИНа пошла в лес собирать грибы Для первого подключа Х используем первые 4 буквы ключа: АЛИН. Переводим исходный текст и первый подключ в двоичную последовательность (см. Приложение Б): исходный текст К 11001010 Р 11010000 Ы 11011011 Л 11001011 О 11001110 В 11000010 А 11000000 пробел 00100000 первый подключ X0 А 11000000 Л 11001011 И 11001000 Н 11001101 Таким образом, первые 64 бита определяют входную последовательность L0: 11001010 11010000 11011011 11001011 R0: 11001110 11000010 11000000 00100000 следующие 32 бита определяют первый подключ Х0: 11000000 11001011 11001000 11001101 I. Найдем значение функции преобразования f(R0, X0) (см. Приложение А) 1). Вычисление суммы R0 и X0 по mod 232 R0: 1100 1110 1100 0010 1100 0000 0010 0000 Х0: 1100 0000 1100 1011 1100 1000 1100 1101 1000 1111 1000 1110 1000 1000 1110 1101 2). Преобразование в блоке подстановки Результат суммирования R0+X0 по mod 232 1000 1111 1000 1110 1000 1000 1110 1101 преобразуем в блоке подстановки (см. Приложение В). Для каждого 4- битного блока вычислим его адрес в таблице подстановки. Номер блока соответствует номеру столбца, десятичное значение блока соответствует номеру строки в таблице. Таким образом, 5-тый блок (1011) заменяется заполнением 11-ой строки и пятого столбца в таблице подстановки (1110). номера блоков 8 7 6 5 4 3 2 1 1000 1111 1000 1110 1000 1000 1110 1101 соответствующие номера строк в таблице подстановки 8 15 8 14 8 8 14 13 заполнение 9 12 3 11 14 14 5 15 результат 1001 1100 0011 1011 1110 1110 0101 1111 3). Циклический сдвиг результата п.2 на 11 бит влево 1101 1111 0111 0010 1111 1100 1110 0001 II. Вычисляем R1=f(R0,X0)L0. Результат преобразования функции f(R0,X0) складываем с L0 по mod2: L0: 1100 1010 1101 0000 1101 1011 1100 1011 f(R0,X0): 1101 1111 0111 0010 1111 1100 1110 0001 R1: 0001 0101 1010 0010 0010 0111 0010 1010 Задание №2. Функция хеширования. Найти хеш–образ своей Фамилии, используя хеш–функцию 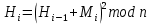 где n = pq, (p и q - простые числа из первой сотни). где n = pq, (p и q - простые числа из первой сотни).Решение Хешируемое сообщение «КРЫЛОВА». Возьмем два простых числа p=13, q=19 (см. Приложение Г). Определим n=pq=13*19=247. Вектор инициализации H0 выберем равным 8 (выбираем случайным образом). Слово «КРЫЛОВА» согласно Приложению Б.2 представлено последовательностью чисел (12, 18, 29, 13, 16, 3, 1) по номерам букв в алфавите. Таким образом, n=247, H0=8, M1=12, M2=18, M3=29, M4=13, M5=16, M6=3, M7=1. Используя формулу Hi Hi1+ Mi2 mod n, получим хеш-образ сообщения «КРЫЛОВА»: H1=(H0+M1)2 mod n = (8 + 12)2mod 247 = 400 mod 247=153 H2=(H1+M2)2 mod n = (153 + 18)2 mod 247 = 29241 mod 247= 95 H3=(H2+M3)2 mod n = (95 + 29)2 mod 247 = 15376 mod 247= 62 H4=(H3+M4)2 mod n = (62 + 13)2 mod 247 = 5625 mod 247= 191 H5=(H4+M5)2 mod n = (191 + 16)2 mod 247 = 42849 mod 247= 118 H6=(H5+M6)2 mod n = (118 + 3)2 mod 247 = 14641 mod 247= 68 H7=(H6+M7)2 mod n = (68 + 1)2 mod 247 = 4761 mod 247= 68 В итоге получаем хеш-образ сообщения «КРЫЛОВА», равный 68. |
