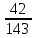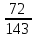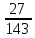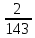Теорвер. ТВ 14.01. Задание 1 Количество двузначных чисел (от 10 до 99) Количество двузначных чисел, не содержащих двойку (на месте десятков может стоять одна из 8 цифр, на месте единиц одна из 9 цифр) Тогда искомая вероятность равна Задание 2
 Скачать 17.29 Kb. Скачать 17.29 Kb.
|
|
Задание 1 Количество двузначных чисел (от 10 до 99): 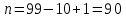 Количество двузначных чисел, не содержащих двойку (на месте десятков может стоять одна из 8 цифр, на месте единиц – одна из 9 цифр): 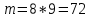 Тогда искомая вероятность равна: 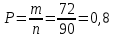 Задание 2 Окружность будет пересекать стороны ромба, которым принадлежит вершина, являющаяся центром окружности, если радиус данной окружности не будет превышать длины стороны ромба. Если сторона ромба равна а, найдем большую диагональ: 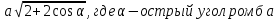 Тогда искомая вероятность равна: 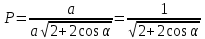 Задание 3 Число тетрадей, которые стоят не дороже 10 руб.: 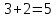 Искомая вероятность равна: 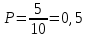 Задание 4 Найдем вероятность по формуле Бернулли: 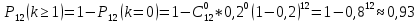 Задание 5 Вероятность извлечь n груш из 13 фруктов (10 груш, 3 - другие) вычислим по следующей формуле: 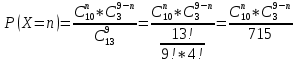 Составим закон распределения вероятностей: 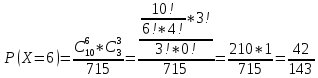 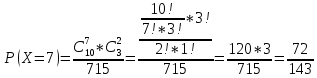 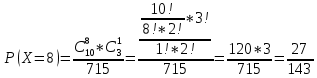 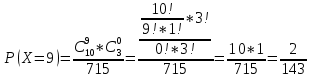
Задание 6 По закону Пуассона: 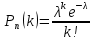 Разложим экспоненту в ряд Маклорена: 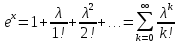 Найдем искомую сумму вероятностей: 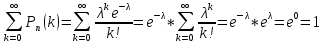 Задание 7 Для оценки вероятности применим неравенство Маркова: 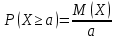 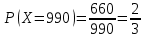 Задание 8 Найдем границы значений случайной величины Х: 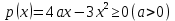 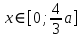 Вычислим параметр a: 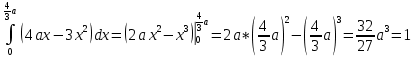 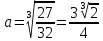 Найдем математическое ожидание: 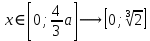 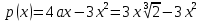 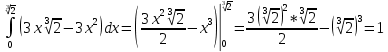 Задание 9 Плотность вероятности заданной случайной величины равна: 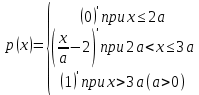 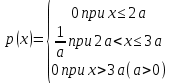 Задание 10 Математическое ожидание решенных задач равно: 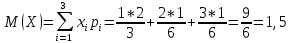 |