Решение задач Ау2.doc (1). Задание 1 Организация ритмичных потоков с кратным ритмом работы бригад Исходные данные

• Название: Задание 1 Организация ритмичных потоков с кратным ритмом работы бригад Исходные данные
• Анкор: Решение задач Ау2.doc (1).docx
• Дата: 27.02.2018
• Размер: 128.12 Kb.
• Имя файла: Решение задач Ау2.doc (1).docx
• Тип: Решение; #15976

ЗАДАНИЕ № 1
Организация ритмичных потоков

с кратным ритмом работы

бригад

Исходные данные.

Количество захваток 12.

Состав работ и количество исполнителей:

- земляные работы – R1 = 4 чел., K1 = 2 дн.;

- устройство песчаного основания – R2 = 6 чел., K2 = 1 дн.;

- установка бортового камня – R3 = 6 чел., K3 =2 дн.;

- устройство бетонной подготовки – R4 = 8 чел., K4 = 1 дн.;

- асфальтирование покрытия – R5 = 8 чел., K5 =2 дн.

Объемы работ на захватках принимаются одинаковыми.

Технологический перерыв τ между устройством бетонной подготовки и асфальтированием покрытия принят равным 6 дням.
Решение

Шаг потока (t) принимаем равным наименьшему ритму работы бригад, т. е.

t = К₂ = К₄ = 1 день.

Общая продолжительность работы всех бригад на одной захватке

определяется как сумма К₁ + К₂ + К₃ + К₄ + К₅.

В данном случае 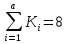дней, где а – число процессов, включённых в

поток. Отсюда находим количество бригад, участвующих в выполнении работ.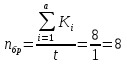

бригад

Используя общую формулу потока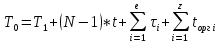



найдём, что общая продолжительность специализированного потока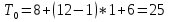

дня

Циклограмма потока строится в осях координат (рис. 1): по оси ординат откладываем необходимое количество захваток, а по оси абсцисс – продолжительность работ в днях. Принимаем необходимый масштаб времени, по оси абсцисс откладываем 25 дней и строим циклограмму специализированного потока:
После построения циклограммы специализированного потока строится диаграмма потребности рабочей силы. В рассматриваемом примере в первый день на первой захватке работает бригада № 1 в составе 4 человек. На второй день на выполнение земляных работ на первой захватке включается бригада № 2 в количестве 4 человек. Таким образом, в специализированный поток включаются всё новые бригады частных потоков. Вследствие этого одновременная численность работающих на объекте возрастает до 42 человек. Период, пока в специализированный поток не включились все 42 человека, носит название периода развёртывания потока.

Время, в течение которого на объекте находится наибольшее (максимальное) количество исполнителей, носит название периода установившегося потока - Т_у. В нашем примере Т_у равен 1 деню.

После периода установившегося потока из специализированного потока начинают исключаться частные потоки, т. е. специализированный поток свёртывается. Период, когда в специализированном потоке уменьшается количество исполнителей, носит название периода свёртывания потока.

На основе диаграммы потребности рабочей силы определяется среднее количество исполнителей в специализированном потоке по формуле: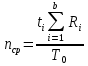



где t_i – продолжительность частного потока с наименьшим ритмом, в днях;

R_i – количество исполнителей в бригаде, выполняющих работы в частном

потоке.

В рассматриваемом примере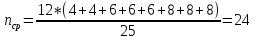
чел.

Определив среднее количество исполнителей в специализированном

потоке, рассчитываем показатель равномерности потока по количеству рабочих

α₁.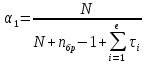



Подставив соответствующие значения, получим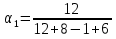

= 0,48

Затем определяем показатель равномерности потока по времени α₂ .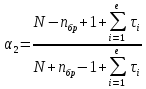



Подставив соответствующие значения, получим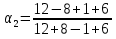

= 0,44

Чем больше α₁, тем равномернее поток. В пределе α₁ стремится к 1. Для установившихся потоков α₁ = 0,48.

Показатель равномерности потока по времени α₂ показывает степень поточности. При значении α₂ ≤ 0,44 периода установившегося потока нет.

ЗАДАНИЕ № 2
Организация неритмичных потоков
Исходные данные:

Общее число захваток – 3.

Состав работ и количество исполнителей:

отрывка котлована под подвал и фундаменты – R1 = 4 чел.;

монтаж фундаментов стен и подвала – R2 = 8 чел.;

монтаж перекрытий над подвалом – R3 = 6 чел.

Работы ведутся в одну смену при постоянном составе бригад.

Трудоёмкость работ по отдельным захваткам различна.

Номер бригады	Ритм работы бригад на захватках
	1	2	3
1	6	7	6
2	4	5	6
3	7	6	5

Решение

Задача может быть решена аналитическим или графическим способом.
2.1. Аналитический способ

Исходя из условия поточного выполнения работ, на одной захватке может работать только одна бригада. Поэтому при организации неритмичных потоков в процессе работ предусматриваются организационные перерывы между работой смежных бригад, или так называемые пустующие захватки. Наличие пустующих захваток является характерным для неритмичных потоков. Сначала строим циклограмму работы первой бригады (рис. 2). Затем определяем интервал времени «с», между началами работ смежных бригад № 1 и № 2 на первой захватке.

Для этого записываем продолжительность работы бригады № 1 нарастающим итогом, начиная с захватки № 2, т. е. составляем ряд чисел: , , .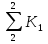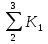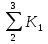

Таким же образом составляем ряд чисел, начиная с захватки № 1, для бригады № 2.

Получившиеся два ряда чисел записываем друг под другом и вычитаем числа второго ряда из чисел первого. Для рассматриваемого варианта это выглядит следующим образом:

Ряд чисел для бригады № 1: 7;13

Ряд чисел для бригады № 2: 7; 13; 18

Разность «а» : 0; 0; -18
Наибольшее положительное значение разности показывает величину организационного перерыва между окончанием и началом работы смежных бригад № 1 и № 2. Интервал между началами работы смежных бригад определится по формуле: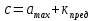



где а_max – наибольшее положительное значение разности чисел рядов;

к_пред – ритм работы предшествующей бригады на первой захватке.

В рассматриваемом примере наибольшая разность равна одному дню,

поэтому с₁ = 0 + 6 = 6 дней.

Откладываем на оси времени полученный интервал, равный 6 дням, от начала координат и находим точку начала работы второй бригады. Затем строим циклограмму работы второй бригады.

Аналогичным способом увязываем работу бригад № 2 и № 3. Нарастающий ряд чисел продолжительности работы для бригады № 2 записываем, начиная с захватки № 2, а для бригады № 3 с захватки № 1.

Ряд чисел для бригады № 2: 5; 11

Ряд чисел для бригады № 3: 4; 9; 15

Разность «а»: +1; +2; -15
Тогда с₂ = 2 + 4 = 6 дней.

Откладываем 6 дней от начала работы бригады № 2 и строим циклограмму работы бригады № 3. В результате получаем циклограмму неритмичного специализированного потока.
На основе циклограммы потока строим диаграмму потребности рабочих.

Общая продолжительность неритмичного специализированного потока определяется по формуле: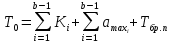



где 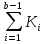- суммарная продолжительность работы всех бригад, за исключением последней, на первой захватке;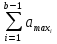

- сумма максимальных разностей между числами рядов смежных бригад;

Т_бр.n - продолжительность работы последней бригады на всех захватках.

В нашем случае Т₀=10+2+18 = 30дней.

Из диаграммы потребности рабочих определим показатель равномерности потока по времени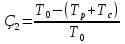



где Т_р – период развертывания потока,

Т_с – период свертывания потока.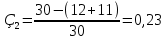



2.2. Графический способ

При графическом способе (рисунок 2) сначала строим циклограмму работы бригады № 1. Затем строим циклограмму работы бригады № 2, планируя начало работы бригады № 2 сразу же после окончания работы бригады № 1 на первой захватке. Затем строим циклограмму работы бригады № 3, планируя начало работы бригады № 3 сразу же после окончания работы бригады № 2 на первой захватке.

ЗАДАНИЕ № 3

Матричный способ расчёта ритмичных потоков
Исходные данные:

Общее число захваток – N=6.

Потоком охвачены следующие работы:

• земляные работы К₁=2;

• устройство песчаного основания К₂=2;

• установка бортового камня К₃=3;

• устройство бетонной подготовки К₄=2;

• работы на асфальтировании покрытия К₅=1.

Работы ведутся в одну смену при постоянном составе бригад.

Трудоёмкость работ на отдельных захватках одинакова.
Решение

Исходные данные записываются в клеточную матрицу (рис. 3). В строках матрицы указываются захватки, а в столбцах – процессы. В центре каждой клетки, представляющей захватку, проставляется продолжительность выполнения соответствующего процесса на захватке. Под клеточной матрицей указывается суммарная продолжительность каждого процесса на всех захватках.

Расчёт ведут по столбцам: для первого процесса всегда сверху вниз, а для последующих в зависимости от суммарной продолжительности процессов на захватках. Если суммарная продолжительность следующего процесса больше предыдущего, то расчёт ведут также сверху вниз, а если меньше – снизу вверх.

В каждой клетке кроме продолжительности (ритма работы бригады) проставляют два значения: в левом верхнем углу – время начала процесса на захватке, в правом нижнем углу – время его окончания.

Время начала первого процесса на первой захватке всегда принимается равным 0 (аналогично началу координат при построении циклограммы поточного строительства). Суммируя время начала процесса с его продолжительностью, определяют время окончания процесса на данной захватке, которое записывают в правом нижнем углу клетки.

В рассматриваемом примере время окончания первого процесса на первой захватке, равное 2, может считаться началом этого процесса на следующей захватке. Поэтому цифру 2 из нижнего правого угла верхней клетки переносим без изменений в верхний левый (накрест лежащий) угол следующей нижней клетки и определяем вышеуказанным способом его окончание на второй захватке. Подобная процедура повторяется на всех захватках до завершения данного процесса. Затем переходим ко второму процессу. Так как его общая продолжительность в рассматриваемом примере равно продолжительности первого (12 =12), то расчёт ведем опять сверху вниз. Поскольку второй процесс на первой захватке можно начать сразу же после окончания на ней первого процесса, то цифру 2 из нижнего угла левой клетки переносим в верхний угол правой клетки в качестве начала второго процесса. Дальше расчёт третьего процесса ведём аналогично первому. В результате получаем, что второй процесс будет закончен на 14-й день, третий на 22-й. Переходя к четвертому процессу, устанавливаем, что его общая продолжительность меньше продолжительности второго (18 > 12). Следовательно, третий и четвертый процессы нужно увязывать, начиная с последней захватки, и вести расчёт снизу вверх. Поэтому цифру 22 из нижнего угла левой клетки переносим в верхний угол правой клетки (четвертый столбец). Одновременно цифру 22 переносим в нижний правый угол

вышележащей клетки, где она показывает окончание пятого процесса на четвертой захватке. Начало его на этой же захватке определится как разность между окончанием процесса и его продолжительностью (22 – 2 = 20). Двигаясь вверх по этому столбцу, в таком же порядке проставляем в каждой клетке сначала окончание, а затем начало выполнения процесса на соответствующей захватке.

Затем заполняем все клетки пятого столбца (снизу вверх).

Цифра (25) в нижнем углу последней клетки показывает общую продолжительность выполнения всей совокупности частных потоков. Разность между началами смежных процессов в клетках показывает величину интервалов между ними. Например, интервал между началами первого и второго процессов на первой захватке составляет 2 дня, между вторым и третьим – 2 дня (4 – 2= 2), между третьим и четвёртым – 8 дней (12 – 4 = 8), между четвёртым и пятым – 7 дней (19 – 12 = 7).

Из рис. 3 можно получить данные о величине организационных перерывов между окончанием предшествующего процесса на одной из захваток и началом на ней следующего. Для этого необходимо определить разность значений накрест лежащих углов двух смежных частных потоков. Например, перерыв между началом выполнения третьего процесса на второй захватке и окончанием на ней второго процесса составит 1 день (7 – 6 = 1). Организационные перерывы отмечены крестиками.
Рис.3 Матричный способ расчета ритмичного потока
ЗАДАНИЕ № 4

Матричный способ расчёта неритмичных потоков
Исходные данные:

Общее число захваток – N=5.

Специализированными потоками охвачены следующие работы:

• подземная часть здания;

• надземная часть здания;

• санитарно-технические работы;

• отделочные работы.

Работы ведутся в одну смену при постоянном составе бригад.

Трудоёмкость работ на отдельных захватках различна.

Номер бригады	Ритм работы бригад на захватках
	1	2	3	4	5
1	6	5	4	3	2
2	5	4	3	2	3
3	4	3	2	3	4
4	4	5	4	3	2

Решение

Исходные данные записываются в клеточную матрицу (рис. 4). Расчёт продолжительности строительства при неритмичном потоке сводится к нахождению такого совмещения выполняемых работ, при котором организационные перерывы в работе смежных бригад на захватках будут минимальными и в тоже время должны обеспечивать беспрепятственное развитие частных потоков на всех захватках. Захватка, на которой следующий процесс начинается без всякой задержки при беспрепятственном развитии его

на всех других захватках, определит место критического сближения двух смежных частных потоков. Если уменьшить или увеличить это сближение, то в первом случае последующий процесс начнётся раньше, чем будет закончен на данной захватке предыдущий процесс; во втором – неоправданно увеличится общий срок строительства.

Расчёт потока ведут с использованием изложенного в задании № 3 алгоритма расчета ритмичных потоков, учитывая некоторые особенности.

В неритмичных потоках проверка увязки с предшествующим потоком является обязательной на каждой захватке. Начало любого процесса на любой захватке, указанное в верхнем левом углу клетки не может быть по своей величине меньше окончания предшествующего процесса на этой захватке, записанного в нижнем углу соседней левой клетки. По ходу расчёта необходимо делать поправки или пытаться найти захватку, с которой следует начать расчёт, руководствуясь следующим правилом:

по каждой паре смежных процессов сопоставляется время их выполнения в диагональных клетках при движении сверху вниз. Если все сроки правого столбца по диагонали будут больше или равны срокам левого столбца, то расчёт следует начинать сверху, а если меньше, то снизу.

Расчёт первого частного потока ведётся всегда сверху вниз.



Рис.4. Матричный способ расчета неритмичного потока

ЗАДАНИЕ № 5

Оптимизация неритмичных потоков с целью сокращения сроков строительства

Исходные данные:

Результат расчёта неритмичного потока, выполненный в задании № 4.
Решение

При организации неритмичных объектных потоков, когда в роли захваток выступают здания (объекты), важно установить оптимальную очередность их возведения, обеспечивающую кратчайший срок строительства.

Количество возможных вариантов, устанавливающих очерёдность возведения объектов, среди которых находится оптимальный, зависит от числа объектов и определяется числом перестановок (К!). Если в нашем примере 4 объекта и нужно решить, при какой очерёдности при прочих равных условиях будет обеспечен кратчайший срок их возведения, то возможно рассмотрение 4! перестановок, т. е. 4 х 3 х 2 х 1 = 24 вариантов. Из этого следует, что путь полного перебора является громоздким и трудоёмким.

В рассматриваемой методике описываются более простые способы, основанные на использовании матричного алгоритма. На рис. 5 приведён расчёт неритмичного потока, выполненный в предыдущем задании № 4, с введением двух дополнительных граф.



Рис. 5. Исходная матрица для оптимизации неритмичного потока

На основании суммарной продолжительности каждого процесса на всех объектах находим поток наибольшей длительности и выделяем его двойной линией (третий процесс). Этот процесс принимается за ведущий, в известной мере, определяющий срок строительства. Затем по каждой строке матрицы подсчитывается время, предшествующее ведущему процессу (Σ t_предш.) и после него (Σ t_посл.). Результаты заносятся в первую дополнительную графу. Если ведущим потоком является первый или последний, то Σ t_предш. или Σ t_посл. соответственно обращаются в ноль.

Помимо Σ t_предш. и Σ t_посл. рекомендуется также определять разность между продолжительностями последнего и первого процессов с записью результатов во вторую дополнительную графу матрицы с соответствующим знаком (см. рисунок 5).

На основании двух дополнительных граф составляется матрица с новой очерёдностью возведения объектов согласно следующему правилу:

В первую строку матрицы записывается объект с наименьшей Σ t_предш.(числитель) и наибольшим положительным значением разности.

В последнюю строку матрицы записывается объект с наименьшим значением Σ t_посл. (знаменатель) и наименьшим значением разности.

Затем заполняются вторая и предпоследняя строки матрицы с условием, чтобы Σ t_предш. и Σ t_посл. постепенно увеличивались при перемещении внутрь матрицы, а значение разности изменялось бы от максимума в первой строке до минимума в последней (см. рис. 6).

Произведённый расчёт показал, что при новой очерёдности возведения

объектов срок строительства сократился на 6 принятых единиц времени по сравнению с первоначальным вариантом.

В случае, если изложенные выше правила распределения объектов по строкам матрицы противоречат друг другу, то рекомендуется применять их порознь, т. е. сначала построить одну матрицу, руководствуясь значениями Σt_предш. и Σ t_посл., а затем другую – по разностям продолжительностей последнего и первого процессов (t_п – t₁).

Указанный метод определения очерёдности строительства объектов в 80% случаев даёт сокращение сроков строительства.

Сокращение сроков строительства может быть достигнуто также за счёт совмещения процессов, когда последующий процесс начинают, не дожидаясь полного окончания предыдущего, путём деления объектов на участки.



Рис. 6. Рациональная очередность возведения объектов