задание 21 егэ. Задание 20. Задачи на логику и смекалку Тип 27 (про множители)
 Скачать 106.04 Kb.
|
|
Задание № 20. Задачи на логику и смекалку Тип № 27 (про множители) Если бы каждый из двух множителей увеличили на 1, их произведение увеличилось бы на 11. На сколько увеличится произведение этих множителей, если каждый из них увеличить на 2? Решение. Пусть a, b — соответственно первое и второе число. При увеличении каждого из множителей на 1 их произведение увеличивается на 11:    Найдём на сколько увеличится произведение этих множителей при увеличении каждого из них на 2:  Таким образом, при увеличении каждого из множителей на 2, их произведение увеличивается на 24. Ответ: 24. Задания для самостоятельного решения 1. Если бы каждый из двух множителей увеличили на 1, их произведение увеличилось бы на 8. На сколько увеличится произведение этих множителей, если каждый из них увеличить на 3? 2. Если бы каждый из двух множителей увеличили на 2, их произведение увеличилось бы на 12. На сколько увеличится произведение этих множителей, если каждый из них увеличить на 3? Тип № 28 (про доски) Взяли несколько досок и распилили их. Всего сделали 11 поперечных распилов, в итоге получилось 16 кусков. Сколько досок взяли? Решение. Каждый поперечный распил добавляет один кусок к уже имеющимся, следовательно, изначально было 16 − 11 = 5 досок. Ответ: 5. Задания для самостоятельного решения 1. Взяли несколько досок и распилили их. Всего сделали 5 поперечных распилов, в итоге получилось 23 куска. Сколько досок взяли? 2. Взяли несколько досок и распилили их. Всего сделали 24 поперечных распила, в итоге получилось 33 куска. Сколько досок взяли? Тип № 25 (про отметки) В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 690. Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2», «3», «4» или «5» и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округлённая по правилам округления? (Например, 3,2 округляется до 3; 4,5 — до 5; а 2,8 — до 3.) Решение. Разложим число 690 на множители так, чтобы получившиеся множители состояли только из чисел 2, 3, 4, 5, и общее количество цифр в произведении было равно пяти: 690 = 2 · 5 · 23 · 3. Следовательно, учитель поставил Пете отметки 2, 5, 2, 3 и 3. Среднее арифметическое этих оценок:  Ответ: 3. Задания для самостоятельного решения 1. В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 3495. Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2», «3», «4» или «5» и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округлённая по правилам округления? (Например, 3,2 округляется до 3; 4,5 — до 5; а 2,8 — до 3.) 2. В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 3530. Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2», «3», «4» или «5» и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округлённая по правилам округления? (Например, 3,2 округляется до 3; 4,5 — до 5; а 2,8 — до 3.) Тип № 26 (про фишки) Петя меняет маленькие фишки на большие. За один обмен он получает 3 большие фишки, отдав 10 маленьких. До обменов у Пети было 100 фишек (среди них были и большие, и маленькие), а после стало 65. Сколько обменов он совершил? Решение. За один обмен количество фишек у Пети уменьшается на 10 − 3 = 7 штук. Следовательно, Петя совершил (100 − 65)/7 = 5 обменов. Ответ: 5. Задания для самостоятельного решения 1. Петя меняет маленькие фишки на большие. За один обмен он получает 6 больших фишек, отдав 9 маленьких. До обменов у Пети было 100 фишек (среди них были и большие, и маленькие), а после стало 79. Сколько обменов он совершил? 2. Петя меняет маленькие фишки на большие. За один обмен он получает 4 большие фишки, отдав 10 маленьких. До обменов у Пети было 100 фишек (среди них были и большие, и маленькие), а после стало 64. Сколько обменов он совершил? Тип № 23 (про столбы) Десять столбов соединены между собой проводами так, что от каждого столба отходит ровно 8 проводов. Сколько всего проводов протянуто между этими десятью столбами? Решение. От каждого столба отходит по 8 проводов, следовательно, всего будет  соединений. Заметим, что каждые два столба связаны одни проводом, поэтому между этими десятью столбами будет протянуто всего  проводов.Ответ: 40. Задания для самостоятельного решения 1. Десять столбов соединены между собой проводами так, что от каждого столба отходит ровно 4 провода. Сколько всего проводов протянуто между этими десятью столбами? 2. Восемь столбов соединены между собой проводами так, что от каждого столба отходит ровно 6 проводов. Сколько всего проводов протянуто между этими восемью столбами? 3. Двенадцать столбов соединены между собой проводами так, что от каждого столба отходит ровно четыре провода. Сколько всего проводов протянуто между этими двенадцатью столбами? Тип № 24 (про договоры) Из десяти стран четыре подписали договор о дружбе ровно с пятью другими странами, а каждая из оставшихся шести — ровно с тремя. Сколько всего было подписано договоров? Решение. Четыре страны поставили 4 · 5 = 20 подписей. А оставшиеся шесть стран поставили 6 · 3 = 18 подписей. Ясно, что договоров в два раза меньше, чем общее количество подписей, то есть всего было подписано (20 + 18)/2 = 19 договоров. Ответ: 19. Задания для самостоятельного решения 1. Из десяти стран семь подписали договор о дружбе ровно с тремя другими странами, а каждая из оставшихся трёх – ровно с семью. Сколько всего было подписано договоров? 2. Из десяти стран семь подписали договор о дружбе ровно с тремя другими странами, а каждая из оставшихся трёх — ровно с семью. Сколько всего было подписано договоров? 3. Из десяти стран семь подписали договор о дружбе ровно с пятью другими странами, а каждая из оставшихся трёх — ровно с семью. Сколько всего было подписано договоров? Тип № 21 (про вазы) На прилавке цветочного магазина стоят 3 вазы с розами: белая, синяя и красная. Слева от красной вазы 15 роз, справа от синей вазы 12 роз. Всего в вазах 22 розы. Сколько роз в белой вазе? Решение. Выясним относительное расположение ваз с розами. Будем обозначать положение вазы соответствующей буквой. Если вазы расположены в порядке Б−С−К, то получится, что в белой и синей вазах в сумме 15 роз, в красной 12 роз, то есть в сумме 27 роз, что противоречит условию задачи. Если вазы располагаются в порядке Б−К−С получаем аналогичное противоречие. Порядок К−Б−С невозможен, потому что тогда справа от синей вазы и слева от красной вазы нет роз. Непротиворечивое расположение ваз: С−Б−К. Будем также обозначать количество роз в вазе соответствующей буквой. Тогда получим систему уравнений: 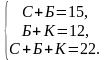 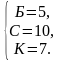 Таким образом, в белой вазе 5 роз. Ответ: 5. Задания для самостоятельного решения 1. На прилавке цветочного магазина стоят 3 вазы с розами: оранжевая, белая и синяя. Слева от синей вазы 15 роз, справа от белой вазы 11 роз. Всего в вазах 23 розы. Сколько роз в оранжевой вазе? 2. На прилавке цветочного магазина стоят 3 вазы с розами: белая, жёлтая и оранжевая. Слева от жёлтой вазы 22 розы, справа от оранжевой вазы 23 розы. Всего в вазах 35 роз. Сколько роз в белой вазе? Тип № 22 (про лучи) Три луча, выходящие из одной точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов. Наибольший угол в 2 раза больше наименьшего. Сколько значений может принимать величина среднего угла? Решение. Пусть α − величина наименьшего угла, β − величина среднего угла, тогда 2α − величина наибольшего угла. Полный угол равен 360°, следовательно, α + β + 2α = 360, откуда β = 360 − 3α. Средний угол должен быть больше меньшего угла и меньше большего, то есть:    Угол β принимает только значения, измеряемые целым числом градусов, поэтому угол β может принимать 90 − 72 − 1 = 17 значений. Ответ: 17. Примечание. Вычитанием единицы в последнем действии учитывается, что значения 72° и 90° не входят в число значений подсчитываемых углов. Задания для самостоятельного решения 1. Три луча, выходящие из одной точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов. Наибольший угол в 6 раз больше наименьшего. Сколько значений может принимать величина среднего угла? 2. Три луча, выходящие из одной точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов. Наибольший угол в 3 раза больше наименьшего. Сколько значений может принимать величина среднего угла? Тип № 19 (про теннис) Миша, Коля и Лёша играют в настольный теннис: игрок, проигравший партию, уступает место игроку, не участвовавшему в ней. В итоге оказалось, что Миша сыграл 9 партий, а Коля — 19. Сколько партий сыграл Лёша? Решение. Больше всех партий сыграл Коля, следовательно, было сыграно не менее 19 партий. В одной из первых двух партий должен был участвовать Миша, значит, было сыграно не более  партии. Значит, Коля участвовал в каждой сыгранной партии. Таким образом, Лёша сыграл 19 − 9 = 10 партий.Ответ: 10. Задания для самостоятельного решения 1. Миша, Коля и Лёша играют в настольный теннис: игрок, проигравший партию, уступает место игроку, не участвовавшему в ней. В итоге оказалось, что Миша сыграл 13 партий, а Коля — 27. Сколько партий сыграл Лёша? 2. Миша, Коля и Лёша играют в настольный теннис: игрок, проигравший партию, уступает место игроку, не участвовавшему в ней. В итоге оказалось, что Миша сыграл 12 партий, а Коля — 25. Сколько партий сыграл Лёша? Тип № 20 (про викторину) Список заданий викторины состоял из 36 вопросов. За каждый правильный ответ ученик получал 5 очков, за неправильный ответ с него списывали 11 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 75 очков, если известно, что по крайней мере один раз он ошибся? Решение. Пусть х – количество верных ответов у – количество неверных ответов. Тогда составим уравнение 5х - 11у = 75, где 0 и 0. Из уравнения видно, что у делится на 5. Пусть: 1)у=5, тогда5х = 75 + 11у= 75 + 55=130,х = 130 : 5 = 26и это меньше 36. 2)у=10,тогда5х =75 +11у=75+110=185, х = 185 : 5=37,но это больше 36. Ответ: 26. Задания для самостоятельного решения 1. Список заданий викторины состоял из 33 вопросов. За каждый правильный ответ ученик получил 7 очков, за неправильный ответ с него списывали 11 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 84 очка, если известно, что по крайней мере один раз он ошибся? 2. Список заданий викторины состоял из 25 вопросов. За каждый правильный ответ ученик получал 5 очков, за неправильный ответ с него списывали 8 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 50 очков, если известно, что по крайней мере один раз он ошибся? 3. Список заданий викторины состоял из 33 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 12 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 70 очков, если известно, что по крайней мере один раз он ошибся? 4. Список заданий викторины состоял из 40 вопросов. За каждый правильный ответ ученик получал 9 очков, за неправильный ответ с него списывали 11 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 171 очко, если известно, что по крайней мере один раз он ошибся? Тип № 17 (про страницы) Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 372, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало? Решение. Из числа 372 можно составить числа 327, 273, 237, 723, 732. Числа 327, 273 и 237 не подходят, поскольку они меньше числа 372. Номер первой страницы после выпавших листов должен быть нечётным, поскольку номер последней страницы перед выпавшими листами чётный. Следовательно, нам подходит только число 723. Вычтем из числа 723 одну страницу, поскольку страница 723 не выпала, а является первой страницей после выпавших листов. Теперь можно найти количество выпавших листов:  Ответ: 175. Задания для самостоятельного решения 1. Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 276, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало? 2. Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 274, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало? 3. Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 294, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало? Тип № 18 (про натуральные числа) Про натуральные числа A, B и С известно, что каждое из них больше 4, но меньше 8. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 165. Какое число было загадано? Решение. Числа А, В и С могут быть равны 5, 6 или 7. Пусть загадали натуральное число Х, тогда Х · А + В – С = 165 или Х · А = 165 + (C – B). Рассмотрим различные случаи. 1) С – В = 0 (7 – 7 = 0, 6 – 6 = 0 или 5 – 5 = 0), тогда Х · А = 165. Число 165 делится нацело на A = 5, значит, Х = 33. 2) С – В = 1 (7 – 6 = 1 или 6 – 5 = 1), тогда Х · А = 166. Число 166 не делится нацело на 5, на 6 и на 7, значит, этот случай не подходит. 3) С – В = –1 (6 – 7 = –1 или 5 – 6 = –1), тогда Х · А = 164. Число 164 не делится нацело на 5, на 6 и на 7, значит, этот случай не подходит. 4) С – В = 2 (7 – 5 = 2), тогда Х · А = 167. Число 167 не делится нацело на 5, на 6 и на 7, значит, этот случай не подходит. 5) С – В = –2 (5 – 7 = –2), тогда Х·А = 163. Число 163 не делится нацело на A = 5, на 6 и на 7, значит, этот случай не подходит. Ответ: 33. Задания для самостоятельного решения 1. Про натуральные числа A, B и С известно, что каждое из них больше 4, но меньше 8. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 417. Какое число было загадано? 2. Про натуральные числа A, B и С известно, что каждое из них больше 4, но меньше 8. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 213. Какое число было загадано? 3. Про натуральные числа A, B и С известно, что каждое из них больше 6, но меньше 10. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 186. Какое число было загадано? Тип № 15 (про Машу и Медведя) Маша и Медведь съели 100 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенья, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну? Решение. 1. Так как варенье и Маша, и Медведь съели поровну, и при этом Медведь ел варенье в 3 раза быстрее, то Маша ела варенье (свою половину) в 3 раза дольше, чем Медведь (такую же половину). 2. Тогда получается, что Медведь ел печенья в 3 раза дольше Маши и к тому же ел их в 3 раза быстрее, то есть, на одно съеденное Машей печенье приходилось 3∙3=9 печений, съеденных Медведем. 3. В сумме эти печенья составляют 1+9=10 и таких сумм в 100 печеньях ровно 100:10 = 10. 4. Значит, Маша съела 10 печений, а Медведь 9∙10=90. Ответ: 90. Задания для самостоятельного решения 1. Маша и Медведь съели 51 печенье и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенья, но в какой-то момент они поменялись. Медведь и то, и другое ест в четыре раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну? 2. Маша и Медведь съели 160 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь - печенье, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенье они съели поровну? 3. Маша и Медведь съели 120 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенье, но в какой-то момент они поменялись. Медведь и то и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну? Тип № 16 (про квас) В магазине квас на разлив можно купить в бутылках, причём стоимость кваса в бутылке складывается из стоимости самой бутылки и кваса, налитого в неё. Цена бутылки не зависит от её объёма. Бутылка кваса объёмом 1 литр стоит 40 рублей, объёмом 2 литра — 70 рублей. Сколько рублей будет стоить бутылка кваса объёмом 0,5 литра? Решение. Пусть стоимость бутылки x руб., стоимость кваса за литр y руб. Имеем систему уравнений:   Значит, бутылка стоит 10 руб., а 1 литр кваса – 30 руб. Тогда бутылка кваса объёмом 0,5 литра будет стоить 10 + 30 · 0,5 = 25 рублей. Тип № 13 (про числа) 1. В таблице три столбца и несколько строк. В каждую клетку таблицы поставили по натуральному числу так, что сумма всех чисел в первом столбце равна 119, во втором - 125, в третьем - 133, а сумма чисел в каждой строке больше 15, но меньше 18. Сколько всего строк в столбце? Решение. Общая сумма во всех столбцах = 119 + 125 + 133 = 377. Числа 18 и 15 не включены в предел, значит: 1) если сумма в строке = 17, то, количество строк равно 377 : 17= 22,2; 2) если сумма в строке = 16, то, количество строк равно 377 : 16= 23,5. Значит, количество строк = 23 (т.к. оно должно быть между 22,2 и 23,5). Ответ: 23. Задания для самостоятельного решения 1. В таблице 3 столбца и несколько строк. В каждую клетку таблицы поставили по натуральному числу так, что сумма всех чисел в первом столбце равна 98, во втором -103, в третьем - 99, а сумма чисел каждой строке больше 26, но меньше 29. Сколько всего строк в таблице? 2. В таблице три столбца и несколько строк. В каждую клетку таблицы вписали по натуральному числу так, что сумма всех чисел в первом столбце равна 72, во втором — 81, в третьем — 91, а сумма чисел в каждой строке больше 13, но меньше 16. Сколько всего строк в таблице? Тип № 14 (про среднее арифметическое) 1. Среднее арифметическое 6 различных натуральных чисел равно 8. На сколько нужно увеличить наибольшее из этих чисел, чтобы их среднее арифметическое стало на 1 больше? Решение. Среднее арифметическое находится как сумма чисел разделенное на их количество. В нашем случае среднее арифметическое равно 8, а количество чисел – 6. Получается, что  , где x – сумма 6 различных натуральных чисел. Отсюда, сумма шести натуральных чисел равна x = 6⋅8 = 48. При увеличении среднего арифметического на 1, т.е. до 9 неважно какое именно число необходимо увеличивать. Посчитаем при среднем арифметическом равном 9, сколько будет сумма 6 различных натуральных чисел  откуда x = 9 ⋅ 6 = 54. Значит, сумму 6 натуральных чисел (в нашем случае наибольшее) необходимо увеличить на 54 − 48 = 6, чтобы среднее арифметическое увеличилось на 1.Ответ: 6. 2. Среднее арифметическое шести различных натуральных чисел равно 8. Среднее арифметическое этих чисел и седьмого числа равно 9. Чему равно седьмое число? Решение. Сумма первых шести чисел равна S6 = 6 · 8 = 48. Запишем выражение для среднего арифметического семи чисел:  Откуда  .Ответ: 15. Задания для самостоятельного решения 1. Среднее арифметическое 7 различных натуральных чисел равно 12. На сколько нужно увеличить наибольшее из этих чисел, чтобы их среднее арифметическое стало на 2 больше? 2. Среднее арифметическое 7 натуральных чисел равно 12. К ним добавили восьмое число такое, что среднее арифметическое этих восьми чисел равно 14. Найдите восьмое число. 3. Среднее арифметическое девяти чисел, записанных на доске, равно 14, а среднее арифметическое первых восьми из этих чисел равно 13. Найдите девятое число, записанное на доске. Тип № 11 (про прямоугольник) 1. Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника. Решение. 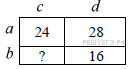 Введём обозначения, как показано на рисунке. Периметр верхнего левого прямоугольника равен 24, поэтому  аналогично,  При помощи полученной системы уравнений выразим значение 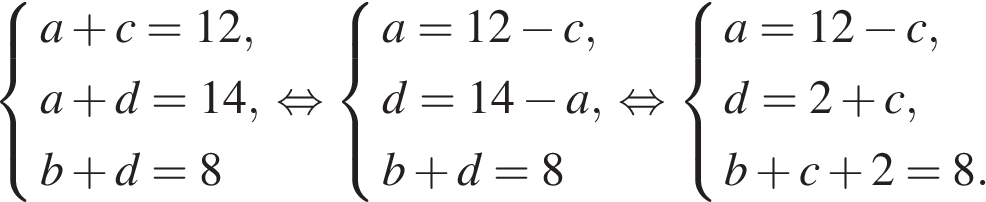  Из третьего уравнения получаем:  Следовательно, искомый периметр равен 12. Ответ: 12. Примечание. Пусть  периметры прямоугольников, рассматриваемых по часовой стрелке с левого верхнего угла. Заметим, что искомый периметр Действительно,  . Значит,  2. Прямоугольник разбит на 4 маленьких прямоугольника двумя прямолинейными разрезами. Площади трёх из них, начиная с верхнего левого и далее по часовой стрелке, равны 9, 12, 32. Найдите площадь четвертого прямоугольника? Решение. 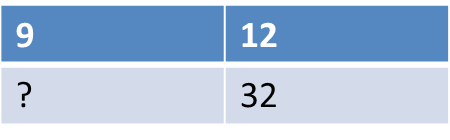 Составим пропорцию:  Ответ: 24. Задания для самостоятельного решения 1. Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 21, 11 и 4. Найдите периметр четвёртого прямоугольника. 2. Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 17, 15 и 18. Найдите периметр четвёртого прямоугольника. 3. Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Площади трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 12, 18 и 30. Найдите площадь четвёртого прямоугольника. 4. Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Площади трёх из них начиная с левого верхнего и далее по часовой стрелке равны 12, 15 и 30. Найдите площадь четвёртого прямоугольника. 5. Прямоугольник разбит на 4 маленьких прямоугольника двумя прямолинейными разрезами. Площади трёх из них, начиная с верхнего левого и далее по часовой стрелке, равны 10, 2, 6. Найдите площадь четвертого прямоугольника? Тип № 12 (про таблицу) Клетки таблицы 6×4 раскрашены в чёрный и белый цвета так, что получилось 19 пар соседних клеток разного цвета и 15 пар соседних клеток чёрного цвета. (Клетки считаются соседними, если у них есть общая сторона.) Сколько пар соседних клеток белого цвета? Решение.
Угловые клетки имеют по 2 соседа, таких клеток в таблице 4, значит, всего пар 2 · 4 = 8. Крайние клетки (не угловые) имеют по 3 пары, таких клеток 12, значит, всего пар 12 · 3 = 36. Все остальные клетки имеют по 4 пары, таких клеток 24 − 4 − 12 = 8, то есть 32 пары. Всего имеем пар 8 + 36 + 32 = 76. В приведенных расчетах все пары взяты дважды (так как учитывались все клетки). Таким образом, уникальных пар 76 : 2 = 38. Поэтому пар белого цвета 38 − 19 − 15 = 4. Ответ: 4. Задания для самостоятельного решения 1. Клетки таблицы 3×8 раскрашены в чёрный и белый цвета так, что получилось 22 пары соседних клеток разного цвета и 11 пар соседних клеток чёрного цвета. (Клетки считаются соседними, если у них есть общая сторона.) Сколько пар соседних клеток белого цвета? 2. Клетки таблицы 4 на 7 раскрашены в чёрный и белый цвета так, что получилось 26 пар соседних клеток разного цвета и 9 пар соседних клеток чёрного цвета. (Клетки считаются соседними, если у них есть общая сторона.) Сколько пар соседних клеток белого цвета? 3. Клетки таблицы 6 х 6 раскрашены в чёрный и белый цвета так, что получилось 30 пар соседних клеток разного цвета и 16 пар соседних клеток чёрного цвета. (Клетки считаются соседними, если у них есть общая сторона.) Сколько пар соседних клеток белого цвета? Тип № 9 (про кольцевую дорогу) На кольцевой дороге расположены четыре бензоколонки: A, B, C и D. Расстояние между A и B — 35 км, между A и C — 20 км, между C и D — 20 км, между D и A — 30 км (все расстояния измеряются вдоль кольцевой дороги в кратчайшую сторону). Найдите расстояние между B и C. Ответ дайте в км. Решение. Расположим А, В, C, D вдоль кольцевой дороги по очереди так, чтобы расстояния соответствовали данным в условии. 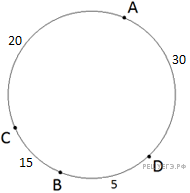 Всё хорошо, кроме расстояния между D и A. Чтобы оно было таким, каким нужно, подвинем D и поставим между B и A нужным образом. Тогда между B и C будет 15 км. Ответ: 15. Задания для самостоятельного решения 1. На кольцевой дороге расположены четыре бензоколонки: A, B, C и D. Расстояние между A и B — 50 км, между A и C — 40 км, между C и D — 25 км, между D и A — 35 км (все расстояния измеряются вдоль кольцевой дороги в кратчайшую сторону). Найдите расстояние между B и C. 2. На кольцевой дороге расположено четыре бензоколонки: А, Б, В и Г. Расстояние между А и Б — 60 км, между А и В — 45 км, между В и Г — 40 км, между Г и А — 35 км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей дуге). Найдите расстояние (в километрах) между Б и В. 3. На кольцевой дороге расположено четыре бензоколонки: А, Б, В и Г. Расстояние между А и Б — 35 км, между А и В — 15 км, между В и Г — 25 км, между Г и А — 30 км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей дуге). Найдите расстояние (в километрах) между Б и В. Тип № 10 (про глобус) На глобусе фломастером проведены 17 параллелей (включая экватор) и 24 меридиана. На сколько частей проведённые линии разделяют поверхность глобуса? Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора. Решение. Представим, что на глобусе ещё не нарисованы параллели и меридианы. Заметим, что 24 меридиана разделят глобус на 24 части. Рассмотрим сектор, образованный двумя соседними меридианами. Проведение первой параллели разделит сектор на две части, проведение второй добавить ещё одну часть, и так далее, таким образом, 17 параллелей разделят сектор на 18 частей. Следовательно, весь глобус будет разбит на 24 · 18 = 432 части. Ответ: 432. Задания для самостоятельного решения 1. На глобусе фломастером проведены 24 параллели (включая экватор) и 17 меридианов. На сколько частей проведённые линии разделяют поверхность глобуса? 2. На поверхности глобуса фломастером проведены 12 параллелей и 22 меридиана. На сколько частей проведённые линии разделили поверхность глобуса? 3. На поверхности глобуса фломастером проведены 13 параллелей и 25 меридианов. На сколько частей проведённые линии разделили поверхность глобуса? Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора. |