Задание 3 Центральное растяжение и сжатие прямых стержней переменного сечения
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
|
Задание 3 Центральное растяжение и сжатие прямых стержней переменного сечения Для стального ступенчатого стержня, рисунок 3.1 находящегося под действием сил 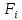 , приложенных в осевом направлении, требуется: , приложенных в осевом направлении, требуется: 1) построить эпюры нормальных сил 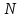 , нормальных напряжений , нормальных напряжений 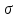 ; ; 2) построить эпюру осевых перемещений 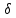 ; ; 3) определить его полное удлинение (укорочение) 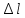 Дано: 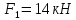 ; ; 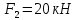 ; ; 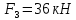 ; ; 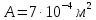 ; ; 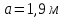 . .Решение. 1. Разбиваем стержень на участки. Под участком понимается часть длины стержня, в пределах которой поперечное сечение и нагрузки не изменяются. В данной задаче таких участков будет три: участок 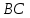 , , 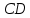 и и 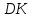 . Для нахождения продольных сил . Для нахождения продольных сил 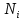 , действующих на каждом участке, воспользуемся методом сечений. , действующих на каждом участке, воспользуемся методом сечений. Рисунок 3.1. 2. Определяем продольные силы в стержне. По правилу знаков продольная сила считается положительной (соответствует растяжению), если она направлена от рассматриваемого поперечного сечения, и отрицательной (соответствует сжатию), если она направлена к сечению. Рассечём стержень на участке 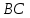 сечением 1-1 на две части и мысленно отбросим левую часть. На оставшуюся часть действует одна сила сечением 1-1 на две части и мысленно отбросим левую часть. На оставшуюся часть действует одна сила 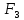 , а действие отброшенной части заменим неизвестной продольной силой , а действие отброшенной части заменим неизвестной продольной силой 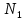 . Если после решения уравнения равновесия сила . Если после решения уравнения равновесия сила 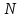 получится со знаком «минус», то направление продольной силы нужно сменить на противоположное – стержень на данном участке испытывает деформацию сжатия. получится со знаком «минус», то направление продольной силы нужно сменить на противоположное – стержень на данном участке испытывает деформацию сжатия.Условие равновесия для оставшейся части стержня: 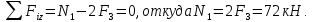 Аналогично определяем продольные силы на других участках. Для участка 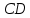 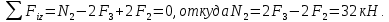 Для участка 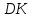 : :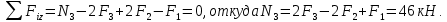 Для построения эпюры продольных сил проведём прямую линию, параллельную оси стержня, и перпендикулярно к ней отложим отрезки, отображающие в некотором масштабе величины продольных сил, возникающих в соответствующих поперечных сечениях стержня. Эпюра продольных сил показана на рис.3.2,а. 3. Определяем нормальные напряжения в поперечных сечениях стержня. Участок 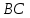 : :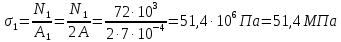 Участок 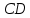 : :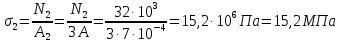 Участок 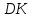 : :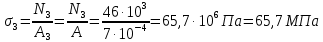 Эпюра нормальных напряжений представлена на рис.3.2,б. Строится она аналогично эпюре продольных сил. 4. Определяем удлинение (укорочение) каждого участка стержня согласно закону Гука и перемещение свободного конца стержня. Участок 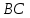 : :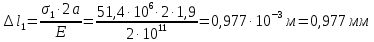 Участок 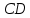 : :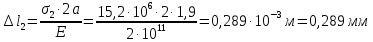 Участок 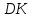 : :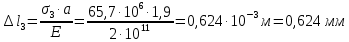 Эпюра перемещений поперечных сечений стержня представлена на рис.3.2,в.  Рисунок 3.2. Перемещение сечения в заделке равно нулю. Перемещение сечения 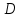 равно удлинению участка равно удлинению участка 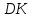 , т.е. , т.е. 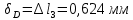 . Перемещение сечения . Перемещение сечения 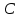 равно алгебраической сумме перемещения сечения равно алгебраической сумме перемещения сечения 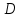 и удлинению участка и удлинению участка 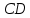 , т.е. , т.е. 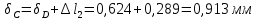 . Перемещение свободного конца стержня (сечения . Перемещение свободного конца стержня (сечения 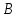 ) будет равно сумме перемещения сечения ) будет равно сумме перемещения сечения 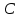 и удлинению участка и удлинению участка 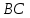 , т.е. , т.е. 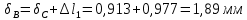 . .Задание 4 Расчет на кручение круглых стержней. Для стального вала, рисунок 4.а, один конец которого условно принят защемленным, при выбранных исходных данных требуется: 1) найти через известные мощности 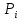 соответствующие скручивающие моменты соответствующие скручивающие моменты 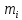 ; ; 2) найти неизвестный момент 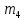 из условия равенства нулю угла поворота свободного конца вала; из условия равенства нулю угла поворота свободного конца вала; 3) построить эпюру крутящих моментов 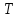 ; ; 4) подобрать круглое и кольцевое (при заданном 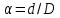 ) сечения из условий прочности; ) сечения из условий прочности; 5) построить эпюры углов поворота 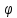 по длине вала круглого сечения; по длине вала круглого сечения;Дано: 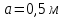 ; ; 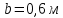 ; ; 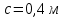 ; ; 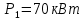 ; ; 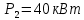 ; ; 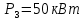 ; ; 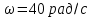 ; ; 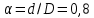 ; ; 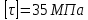 ; ; 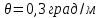 . .Решение. 1. Определяем значения моментов 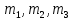 : :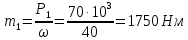 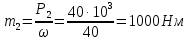 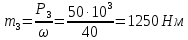 2.Определение величины неизвестного крутящего момента 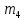 . .Брус жестко заделан левым концом A, правый конец E свободный. В сечениях B, C, и D приложены известные крутящие моменты. Для определения неизвестного момента 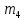 используем условие равенства нулю угла поворота сечения Е. используем условие равенства нулю угла поворота сечения Е.Угол поворота сечения Е относительно сечения A определяется как сумма углов закручивания отдельных участков: 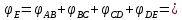 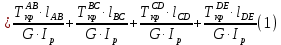  Рисунок 4. Вычисляем крутящие моменты, начиная с незакрепленного конца: 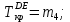 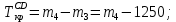 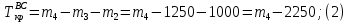 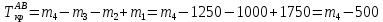 Используя выражения (2) и сокращая на 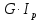 , приводим уравнение (1) к виду: , приводим уравнение (1) к виду: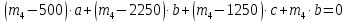 Подставляя значения a, b, c и решая это уравнение, получаем 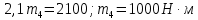 3. Построение эпюры крутящих моментов. Найденное значение 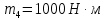 подставляем в выражения (2), вычисляя таким образом величину крутящего момента на каждом участке: подставляем в выражения (2), вычисляя таким образом величину крутящего момента на каждом участке: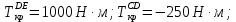 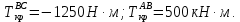 По найденным значениям 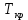 строим эпюру крутящих моментов. Для этого рассматриваем последовательно участки ED, DC, CB и CA. Крутящие моменты, действующие на этих участках, уже вычислены. Величина крутящего момента на каждом участке не зависит от положения сечения в пределах участка (крутящий момент постоянен), поэтому эпюра крутящих моментов ограничена отрезками прямых (рис. 4.б). Построенная эпюра позволяет найти опасное сечение, т.е. такое, в котором действует максимальный (по модулю) крутящий момент. строим эпюру крутящих моментов. Для этого рассматриваем последовательно участки ED, DC, CB и CA. Крутящие моменты, действующие на этих участках, уже вычислены. Величина крутящего момента на каждом участке не зависит от положения сечения в пределах участка (крутящий момент постоянен), поэтому эпюра крутящих моментов ограничена отрезками прямых (рис. 4.б). Построенная эпюра позволяет найти опасное сечение, т.е. такое, в котором действует максимальный (по модулю) крутящий момент.В рассматриваемом примере опасными будут сечения в пределах участка BC; расчетное значение крутящего момента 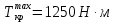 4. Подбор диаметра поперечного сечения бруса. Используем условие прочности: 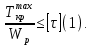 Учитывая, что для круглого сечения 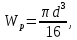 выразим диаметр из условия прочности 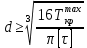 Подставляя 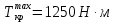 и и 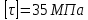 , вычисляем диаметр поперечного сечения, округляя его до стандартной величины: , вычисляем диаметр поперечного сечения, округляя его до стандартной величины: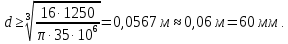 Сечение в форме толстостенного кольца с наружным D и внутренним 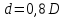 диаметрами. Подставив в (1) зависимость диаметрами. Подставив в (1) зависимость 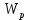 для толстостенного кольца, получим: для толстостенного кольца, получим: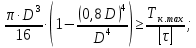 Откуда 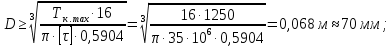 5. Построение эпюры углов закручивания. Определим предварительно величину полярного момента инерции бруса: 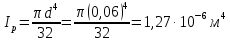 Вычисляем углы закручивания по участкам, принимая модуль сдвига для стали 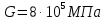 : :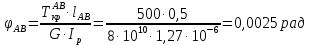 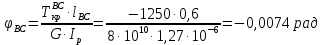 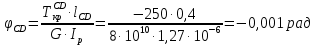 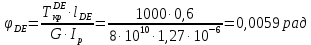 Угол поворота каждого сечения равен сумме углов закручивания соответствующих участков бруса. Суммирование углов начинаем с закрепленного конца A: 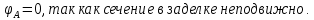 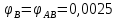 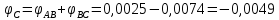 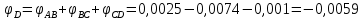 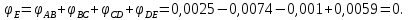 По вычисленным углам поворота сечений построена эпюра углов закручивания (рис. 4.в). Равенство 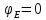 является проверкой решения, так как неизвестный крутящий момент является проверкой решения, так как неизвестный крутящий момент 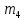 определялся из условия равенства нулю угла поворота свободного конца бруса. определялся из условия равенства нулю угла поворота свободного конца бруса.Задание 5 Плоский изгиб балочных систем. Для заданной балки требуется: 1) построить эпюры поперечных сил 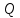 , изгибающих моментов , изгибающих моментов 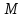 ; ; 2) подобрать круглое сечение, материал балки – дерево 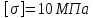 ; ;Дано: 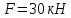 ; ; 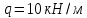 ; ; 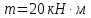 ; ; 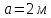 ; ; 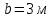 ; ; 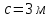 . .Решение. 1. Освобождаем балку от связей, заменяя их действие на балку опорными вертикальными реакциями 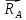 и и 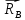 . . Балка находится в равновесии. Составим уравнения равновесия: 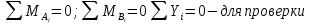 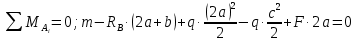 Из этого уравнения находим значение 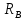 : :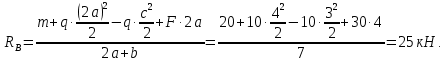 Далее 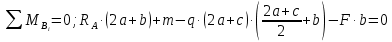 Из этого уравнения определяем 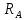 : :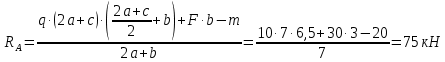 Произведём проверку найденных значений реакций. Составим уравнение проекций всех сил на ось у 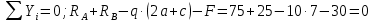 Равенство верное. Следовательно, реакции определены правильно. 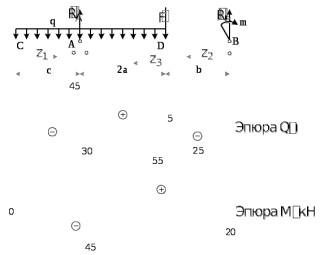 2. Определим значение поперечной силы Q в сечении на участке AC, рассматривая левую часть балки. Поперечная сила в сечении численно равна алгебраической сумме всех внешних сил, действующих на рассматриваемую часть балки. 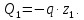 Это уравнение наклонной прямой. Чтобы ее построить, определим две точки на концах участка: 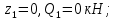 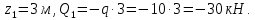 Откладываем наклонную прямую по этим точкам. Дальнейшее решение будем выполнять справа. Определим Qмежду Bи D: 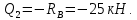 Так как 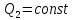 , то на эпюре , то на эпюре 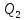 изображается горизонтальной прямой. изображается горизонтальной прямой.Определим Qмежду Cи D: 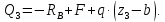 Это уравнение наклонной прямой. Чтобы ее построить, определим две точки на концах участка: 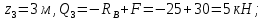 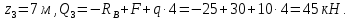 Откладываем наклонную прямую по этим точкам. Определим изгибающий момент на первом участке. Изгибающий момент в сечении равен алгебраической сумме всех внешних моментов, вычисленных относительно сечения и приложенных к рассматриваемой части балки: 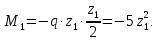 Это уравнение параболы, так как z во второй степени. Для построения параболы необходимо определить 2 точки по краям участка. Парабола строится дугой навстречу распределенной нагрузке. При 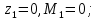 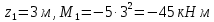 На втором участке: 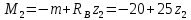 Это уравнение наклонной прямой. При 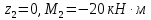 ; ;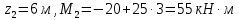 На третьем участке 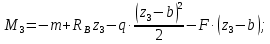 Это уравнение параболы. 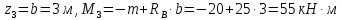 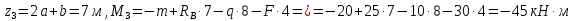 По эпюре 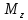 находим опасное сечение балки - сечение, в котором изгибающий момент максимален по абсолютной величине. Для заданной балки изгибающий момент в опасном сечении находим опасное сечение балки - сечение, в котором изгибающий момент максимален по абсолютной величине. Для заданной балки изгибающий момент в опасном сечении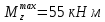 Из условия прочности определим требуемый момент сопротивления сечения: 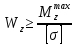 Тогда 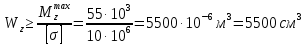 Круглое поперечное сечение имеет момент сопротивления: 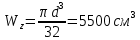 Диаметр круга 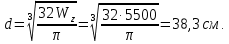 |
