Домашнее задание по теории множеств_заочники. Задание на дом. Повторить теоретический материал Изобразить пары множеств на числовой прямой и записать, какое из них является подмножеством другого 2) А( 3, В(6 3 6 (А В
 Скачать 309.33 Kb. Скачать 309.33 Kb.
|
|
Домашнее задание по теории множеств заочники Задание на дом. 1. Повторить теоретический материал 2. Изобразить пары множеств на числовой прямой и записать, какое из них является подмножеством другого: 2) А=(-; 3], В=(-;6];      3 6 (А В) 3) А=(-2; 5], В=[0; 4);          -2 0 4 5 (В А) 5) А=(-;4), В=[0; 1];        0 1 4 (В А) 6) А=[2; ), В=[3; 6).  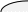 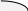     2 3 6 (В А) 3. Изобразите на числовой прямой следующие множества: 1)Х=[1; 4] 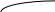 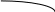    1 4 2) Х={1; 2; 3};      1 3 3) Х=(-2; 2];      -2 2 4) Х=[-1; 3]; 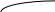 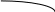    -1 3 5) Х=(-;1]; 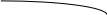   1 6) Х=[-1; ); 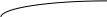   -1 4. Верны ли записи ? : а) {1; 7}{{1; 4; 3},{1; 2}, 7; 1}; ДА т.к. во втором множестве содержатся все элементы первого множества б) {1; 4}{{1; 4; 3},{1; 2}, 1,4}; НЕТ т.к второе множество не содержит элемент {1; 4} в) {1; 3}{{1; 2; 3},{1; 3}, 1}; ДА т.к второе множество содержит элемент {1; 3} г){1; 2}{{1; 2; 5},{1; 5}, 1; 5} НЕТ т.к второе множество не содержит все элементы из первого множества 5. Пусть даны множества А, В, С. Найдите АВ, АС, ВС, АВ, АC, ВС, если: А={2; 3; 8; 9}, В={16; 18; 20}, C=N; АВ=Ø; АС={2; 3; 8; 9}; ВС={16; 18; 20}; АВ={2; 3; 8; 9; 16; 18; 20}; АC=N; ВС=N A=N, B={-2; -1; 0; 1; 2}, C={3; 5; 7}; АВ ={1; 2}; АС ={3; 5; 7}; ВС=Ø; АВ={-2; -1; 0; N}; АC=N; ВС={-2; -1; 0; 1; 2; 3; 5; 7} A={3; 4; 5; ...}, B=N, C={-1; 0; 1; 2}; АВ={3; 4; 5; ...}; АС=Ø; ВС={1; 2}; АВ=N; АC={-1; 0; 1; 2; 3; 4; 5; ...}; ВС={-1; 0; N} A=Z, B={2; 4; 6}, C=N; АВ={2; 4; 6}; АС=N; ВС={2; 4; 6}; АВ=Z; АC=Z; ВС=N A=N, B={-1; 0; 1; 2}, C={15; 16; ...; 20}; АВ={1; 2}; АС={15; 16; ...; 20}; ВС=Ø; АВ={-1; 0; N}; АC=N; ВС={-1; 0; 1; 2; 15; 16; ...; 20} A=Z, B=N, C=Q; АВ=N; АС=Z; ВС=N; АВ=Z; АC=Q; ВС=Q 6. Постройте круги Эйлера для множеств А, В, С и укажите характеристическое свойство элементов множества АВС. В каждом из случаев выделите на чертеже область, изображающую множество АВС, и начертите фигуру, принадлежащую этому множеству: 1) А - множество правильных многоугольников, В - множество треугольников, С - множество четырехугольников; 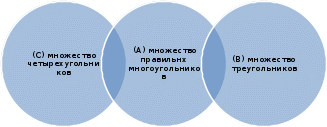 АВС=Ø 2) А - множество параллелограммов, В - множество прямоугольников, С - множество четырехугольников;  АВС=множество ПРЯМОУГОЛЬНИКОВ 3) А - множество прямоугольных треугольников, В - множество равнобедренных треугольников, С - множество равносторонних треугольников; 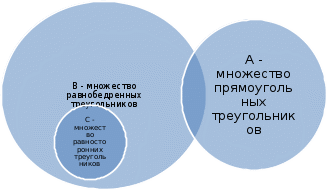 АВС=Ø 4) А - множество прямоугольных треугольников, В - множество равнобедренных треугольников, С - множество треугольников.  АВС=множество РАВНОБЕДРЕННЫХ И ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ 7. Найти пересечение и объединение множеств: [3; 4] и [2; 6]; 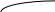 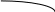   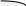     2 3 4 6 [3; 4][2; 6]=[3; 4]; [3; 4][2; 6]=[2; 6] 5)(-1; 3) и (-4; 2]; 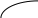 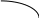  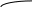      -4 -1 2 3 -4 -1 2 3(-1; 3)(-4; 2]=(-1; 2]; (-1; 3)(-4; 2]=[-4; 3) 2) (-2; 1] и [-2; 0);          -2 0 1 -2 0 1(-2; 1][-2; 0)=(-2; 0); (-2; 1][-2; 0)=[-2; 1] 6)(-; 3) и (-1; ); 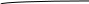 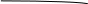 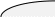 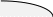    -1 3 (-; 3)(-1; )=(-1; 3); (-; 3)(-1; )=(-; +) 3)(2; ) и [-1; 3];          -1 2 3 -1 2 3(2; )[-1; 3]=(2; 3]; (2; )[-1; 3]=[-1; ) [0; 2] и [1; 3);    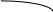      0 1 2 3 [0; 2][1; 3)=(1; 2]; [0; 2][1; 3)=[0; 3) 4) (-; 3] и (-1; +); 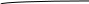 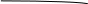 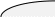     -1 3 (-; 3)(-1; +)=(-1; 3); (-; 3)(-1; +)=(-; +) 8) [-1; 4] и (2; 5].          -1 2 4 5 -1 2 4 5[-1; 4](2; 5]=(2; 4]; [-1; 4] (2; 5]=[-1; 5] Указание. Для решения использовать числовую прямую (3) (рис. 20).         -1 0 2 3 -1 0 2 3(2; )[-1; 3]=(2; 3]; (2; )[-1; 3]=[-1; ) 8. Найдите для каждой тройки множеств А, В, С результаты операции: 1) А(ВС); 2)А(ВС); 3)(АВ)С; 4)(АС)(АВ); 5) (АС)В; 6) (АВ)С, если: а) А={2; 3; 4}, B={3; 6}, C=N; 1) А(ВС)={2; 3; 4}; 2) А(ВС)={2; 3; 4; 6}; 3) (АВ)С={2; 3; 4; 6}; 4) (АС)(АВ)={2; 3; 4}; 5) (АС)В={3; 6}; 6) (АВ)С={N} б) A=N, B=Z, C={-1; 0; 1}; 1) А(ВС)={N}; 2) А(ВС)={-1; 0; N}; 3) (АВ)С={-1; 0; 1}; 4) (АС)(АВ)={N}; 5) (АС)В={-1; 0; N}; 6) (АВ)С={-1; 0; N} в) A={1; 3; 5; ...}, B={2; 4; 6; ...}, C=N; 1) А(ВС)=Ø; 2) А(ВС)={N}; 3) (АВ)С={N}; 4) (АС)(АВ)={1; 3; 5; ...}; 5) (АС)В={2; 4; 6; ...}; 6) (АВ)С={N} г) A=Z, B=N, C={3; 6; 9; ...}; 1) А(ВС)={N}; 2) А(ВС)={Z}; 3) (АВ)С={3; 6; 9; ...}; 4) (АС)(АВ)={N}; 5) (АС)В={N}; 6) (АВ)С={N} 9. Изобразить с помощью кругов Эйлера следующие множества, если АU, BU, CU, ABC: 1) АВС; 4) АВС; 2) (АВ)С; 5) (АВ)(АС); 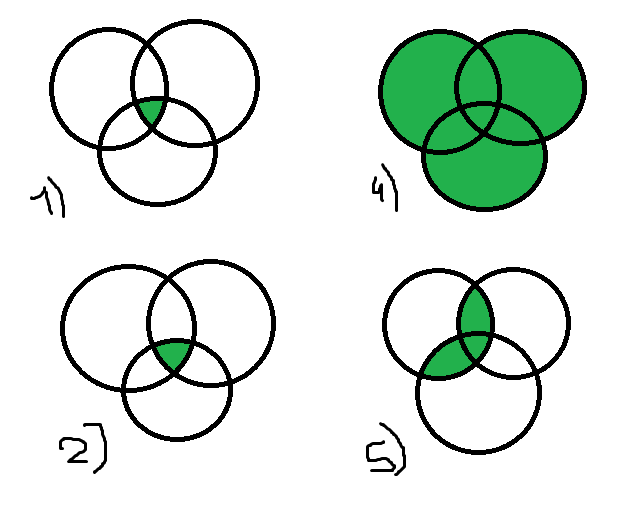 10. Пусть даны множества А, В, С и 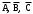 - дополнения соответствующих множеств А, В, С до универсального множества U. Изобразите при помощи кругов Эйлера следующие множества: (АВС): - дополнения соответствующих множеств А, В, С до универсального множества U. Изобразите при помощи кругов Эйлера следующие множества: (АВС):1) 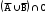 ; 5) ; 5) 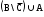 ; ;2) 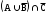 ; 6) ; 6) 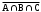 ; ;3) 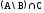 ; 7) ; 7) 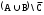 ; ;4) 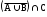 ; 8) ; 8) 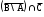 ; ;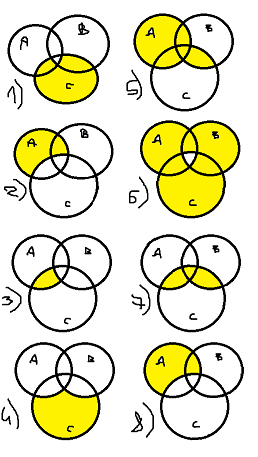 11. Используя круги Эйлера докажите следующие равенства: 3) 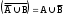 ; ;4) 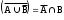 ; ;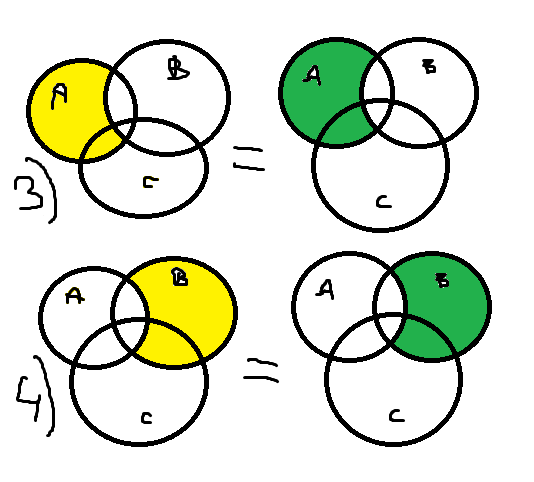 12. Найдите декартово произведение множеств А и В и изобразите их элементы на координатной плоскости, если: 1) A={1; 2; 3}; B={3; 4}; 2) A=N, B={3; 4}; 3) A={3}, B=(2; 5); 4) A={1; 2; 3}, B=Z; 5) A=Z, B=N; 6) A=N, B=(3; 4]; 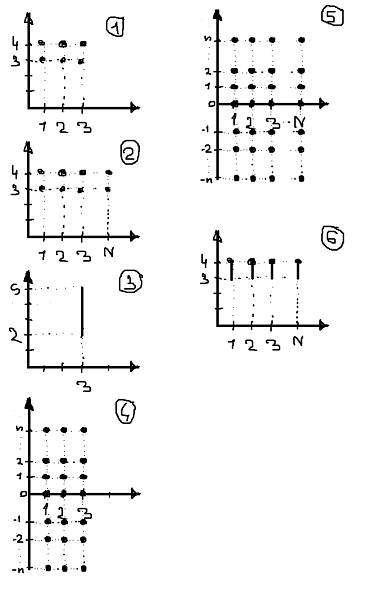 13. Перечислите элементы булеана множества A={1, 4, {1, 4}}. Проверьте, что A и B(A) имеют общий элемент. B(A) = { Ø, {1}, {4}, {{1, 4}}, {1,4}, {1, {1,4}}, {4, {1,4}}, {1, 4, {1,4}} } Общий элемент - {1, 4} |
