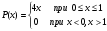ЗАДАНИЕ НА КОНТРОЛЬНУЮ РАБОТУ
ДЛЯ ЗАОЧНОГО ОТДЕЛЕНИЯ
Задание на контрольную работу выбирается согласно последней цифре шифра (см. таблицу 1).
Таблица 1.
Последняя цифра шифра
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
Задачи
|
2, 11, 21,
33, 47
|
5, 18, 28, 36, 43
|
7, 15, 23, 31, 48
|
1, 20, 25, 40, 46
|
8, 12, 30, 35, 42
|
3, 16, 22, 38, 49
|
10, 19, 27, 32, 44
|
6, 13, 29, 37, 41
|
4, 17, 24, 39, 50
|
9, 14, 26, 34, 45
|
Найдите функцию правдоподобия для следующих данных: Вероятность появления цели в зоне РЛС: Р(Uц) = 0,25; Вероятность обнаружения сигнала от цели: Р(Uc/Uц) = L(Uц) = 0,7; Вероятность появления ложного сигнала от помех: Р(Uc/Uп) = L(Uп) = 0,06. Вычислив функцию правдоподобия, определить, есть в принятой реализации сигнал или его нет.
Импульс прямоугольной формы, длительностью τи заполнен гармоническим колебанием U(t) = Ucosɷ0t. Его можно представить в виде:
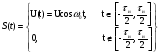
Считать, что длительность импульса τи много больше частоты заполнения Т0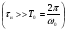 . Найти энергию радиоимпульса и сравнить её с энергией видеоимпульса. Привести спектры видео и радиоимпульса. . Найти энергию радиоимпульса и сравнить её с энергией видеоимпульса. Привести спектры видео и радиоимпульса.
Случайная величина Х треугольного вида (рис.1) имеет плотность вероятности, которую можно представить выражением:
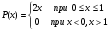
Определить математическое ожидание, дисперсию и среднее квадратическое отклонение случайно величины Х.
Плотность вероятности случайной величины Х треугольного вида с условием нормировки имеет вид:
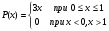
Найти функцию распределения F(x) и построить график зависимости F(x), как функцию от х.
По данным ремонтной мастерской в среднем из 100 отказов телевизора 50% обусловлено выходом из строя электронных ламп, 15% - конденсаторов, 12% - резисторов, 5% - кинескопов, а остальные отказы обусловлены другими причинами.
Найти вероятность Р(А) отказа телевизора по другим причинам.
Обнаружение воздушной цели производиться независимо двумя радиолокационными станциями. Вероятность Р(А) обнаружения цели первой станцией равна 0,7. Вероятность Р(В) обнаружения цели второй станцией равна 0,8.
Найти вероятность Р(С) того, что цель будет обнаружена хотя бы одной станцией.
Каждая буква «МАТЕМАТИКА» написана на отдельной карточке, карточки тщательно перемешаны. Последовательно извлекаются четыре карточки.
Какова вероятность Р(А) получить слово «ТЕМА»?
Два стрелка стреляют по очереди по мишени до первого попадания. Каждый из них имеет право сделать не более двух выстрелов. Зная, что при одном выстреле первый стрелок попадает в мишень с вероятностью р1, а второй – р2.
Найти вероятность того, что первый стрелок попадает в мишень.
Система управления состоит из четырех узлов А1, А2, А3 и А4 (рис. 1). Вероятность рi безотказной работы узлов соответственно равны р1, р2, р3 и р4.
Вычислить вероятность безотказной работы Р всей системы управления
А1
А2
А3
А4
Рис. 1
Вероятность того, что параметры одного из трех блоков радиостанции (антенно-фидерное устройства, приемника или передатчика) выйдут из строя за время полета самолета из допусков, равны соответственно 0,1; 0,2 и 0,3. Если из поля допусков вышли параметры одного блока, связь не будет установлена с вероятностью 0,25, если двух, то 0,4, если трех, то 0,5.
Найти вероятность Р(А) того, что связь не будет установлена.
По каналу связи, подверженному воздействию помех, передается одна из команд управления в виде кодовых комбинаций 11111 или 00000, причем априорные вероятности передачи этих команд соответственно равны 0,7 и 0,3. Из-за наличия помех вероятность правильного приема каждого из символов (1 и 0) уменьшается до 0,6. Предполагается, что символы кодовых комбинаций искажаются независимо друг от друга. На выходе приемного устройства зарегистрирована комбинация 10110. Определить какая команда была передана (11111 или 00000).
Истребитель атакует базу противника, в составе которого 6 носителей и 3 постановщика помех, внешне друг от друга не различимых.
Найти вероятность того, что атакованный самолет является носителем.
В студии имеются три телевизионных камеры. Вероятность того, что каждая камера работает в данный момент времени, равна 0,6.
Найти вероятность того, что в данный момент времени включена хотя бы одна камера.
Два из трех независимо работающих элементов вычислительного устройства отказали.
Вычислить вероятность того, что отказали первый и второй элементы, если вероятности отказа первого, второго и третьего элементов соответственно равны 0,2; 0,4; 0,3.
На пяти одинаковых карточках написаны цифры 1, 2, 3, 4, 5. Две из них наугад вынимаются одна за другой.
Найти вероятность того, что сумма цифр на вынутых карточках является нечетным числом.
При испытаниях 200 случайно отобранных резисторов в течении времени t оказалось, что относительная частота исправных резисторов равна 0,95.
Определить число исправных резисторов.
Проводится бомбометание по трем складам боеприпасов, причем сбрасывается одна бомба. Вероятность попадание в первый склад равна 0,01, во второй – 0,008, в третий – 0,025. При попадании в один из складов взрываются все три.
Определить вероятность того, что склады будут взорваны.
Вероятность разрегулировки датчика опорных частот, передатчика, приемника и антенно-фидерного тракта за время Т работы радиостанции соответственно равны 0,4; 0,2; 0,3; 0,3.
Найти вероятность отказа радиостанции за время Т, если из-за регулировки одного блока радиостанция отказывает с вероятностью 0,3, из-за разрегулировки двух блоков – 0,5, трех блоков – 0,7, четырех – 0,9.
Рассчитать величину верхнего и нижнего порога для обнаружителя Вальда-Вольфовича, если вероятность ложной тревоги РЛТ = 10-4, а вероятность правильного обнаружения D = 0,9.
Сигнал обрабатывается с помощью согласованного фильтра. Гауссов шум имеет спектральную мощность N0 = 3*10-12 В2с. Половина длительности импульса τи = 9 мкс. Определить при какой амплитуде импульса на выходе согласованного фильтра будет достигнуто соотношение сигнал/шум, равное q = 10.
Найдите функцию правдоподобия для следующих данных: Вероятность появления помехи в зоне РЛС: Р(UП) = 0,60; Вероятность обнаружения сигнала от цели: Р(Uc/Uц) = 0,6; Вероятность появления ложного сигнала от помех: Р(Uc/Uп) = 0,07. Вычислив функцию правдоподобия, определить, есть в принятой реализации сигнал или его нет.
Плотность вероятности случайной величины Х треугольного вида с условием нормировки имеет вид:
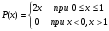
Найти функцию распределения F(x) и построить график зависимости F(x), как функцию от х.
Случайная величина Х треугольного вида (рис.1) имеет плотность вероятности, которую можно представить выражением:
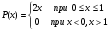
Определить математическое ожидание, дисперсию и среднее квадратическое отклонение случайно величины Х.
Каждая буква «МАТЕМАТИКА» написана на отдельной карточке, карточки тщательно перемешаны. Последовательно извлекаются четыре карточки.
Какова вероятность Р(А) получить слово «МАМА»?
Обнаружение воздушной цели производиться независимо двумя радиолокационными станциями. Вероятность Р(А) обнаружения цели первой станцией равна 0,6. Вероятность Р(В) обнаружения цели второй станцией равна 0,7.
Найти вероятность Р(С) того, что цель будет обнаружена хотя бы одной станцией.
Два стрелка стреляют по очереди по мишени до первого попадания. Каждый из них имеет право сделать не более двух выстрелов. Зная, что при одном выстреле первый стрелок попадает в мишень с вероятностью р1, а второй – р2.
Найти вероятность того, что второй стрелок попадает в мишень.
Система управления состоит из четырех узлов А1, А2, А3 и А4 (рис. 2). Вероятность рi безотказной работы узлов соответственно равны р1, р2, р3 и р4.
Вычислить вероятность безотказной работы Р всей системы управления
А3
А4
А1
А2
Рис. 2
Вероятность того, что параметры одного из трех блоков радиостанции (антенно-фидерное устройства, приемника или передатчика) выйдут из строя за время полета самолета из допусков, равны соответственно 0,1; 0,2 и 0,3. Если из поля допусков вышли параметры одного блока, связь не будет установлена с вероятностью 0,25, если двух, то 0,4, если трех, то 0,5.
Найти вероятность Р(А) того, что связь не будет установлена.
Система управления состоит из четырех узлов С1, С2, С3 и С4 (рис. 3). Вероятность рi безотказной работы узлов соответственно равны р1, р2, р3 и р4.
Вычислить вероятность безотказной работы Р всей системы управления
С4
С1
С2
С3
Рис.3
В студии имеются три телевизионных камеры. Вероятность того, что каждая камера работает в данный момент времени, равна 0,6.
Найти вероятность того, что в данный момент времени включена хотя бы одна камера.
Истребитель атакует базу противника, в составе которого 5 носителей и 2 постановщика помех, внешне друг от друга не различимых.
Найти вероятность того, что атакованный самолет является носителем.
Два из трех независимо работающих элементов вычислительного устройства отказали.
Вычислить вероятность того, что отказали первый и второй элементы, если вероятности отказа первого, второго и третьего элементов соответственно равны 0,3; 0,2; 0,4.
На пяти одинаковых карточках написаны цифры 1, 2, 3, 4, 5. Две из них наугад вынимаются одна за другой.
Найти вероятность того, что вторая цифра меньше первой.
На пяти одинаковых карточках написаны цифры 1, 2, 3, 4, 5. Две из них наугад вынимаются одна за другой.
Найти вероятность того, что вторая цифра больше первой.
Число исправных резисторов в партии 240 штук, их вероятность относительно общего числа резисторов в партии 0,8.
Определить общее число резисторов в партии.
Рассчитать величину верхнего и нижнего порога для обнаружителя Вальда-Вольфовича, если вероятность ложной тревоги РЛТ = 10-3, а вероятность правильного обнаружения D = 0,7.
Вероятность разрегулировки датчика опорных частот, передатчика, приемника и антенно-фидерного тракта за время Т работы радиостанции соответственно равны 0,4; 0,2; 0,3; 0,3.
Найти вероятность отказа радиостанции за время Т, если из-за регулировки одного блока радиостанция отказывает с вероятностью 0,3, из-за разрегулировки двух блоков – 0,5, трех блоков – 0,7, четырех – 0,9.
По данным ремонтной мастерской в среднем из 100 отказов телевизора 40% обусловлено выходом из строя электронных ламп, 10% - конденсаторов, 15% - резисторов, 3% - кинескопов, а остальные отказы обусловлены другими причинами.
Найти вероятность Р(А) отказа телевизора по другим причинам.
Два из трех независимо работающих элементов вычислительного устройства отказали.
Вычислить вероятность того, что отказали третий и второй элементы, если вероятности отказа первого, второго и третьего элементов соответственно равны 0,3; 0,2; 0,3.
Проводится бомбометание по трем складам боеприпасов, причем сбрасывается одна бомба. Вероятность попадание в первый склад равна 0,01, во второй – 0,008, в третий – 0,025. При попадании в один из складов взрываются все три.
Определить вероятность того, что склады будут взорваны.
Каждая буква слова «АКВААЭРОБИКА» написана на отдельной карточке, карточки тщательно перемешаны. Последовательно извлекаются четыре карточки.
Какова вероятность Р(А) получить слово «КРАБ»?
Импульс прямоугольной формы, длительностью τи заполнен гармоническим колебанием U(t) = Usinɷ0t. Его можно представить в виде:
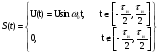
Считать, что длительность импульса τи много больше частоты заполнения Т0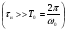 . Найти энергию радиоимпульса и сравнить её с энергией видеоимпульса. Привести спектры видео и радиоимпульса. . Найти энергию радиоимпульса и сравнить её с энергией видеоимпульса. Привести спектры видео и радиоимпульса.
Обнаружение воздушной цели производиться независимо тремя радиолокационными станциями. Вероятность Р(А) обнаружения цели первой станцией равна 0,7. Вероятность Р(В) обнаружения цели второй станцией равна 0,8. Вероятность Р(С) обнаружения цели третьей станцией равна 0,6.
Найти вероятность Р(D) того, что цель будет обнаружена хотя бы одной станцией.
Найдите функцию правдоподобия для следующих данных: Вероятность появления цели в зоне РЛС: Р(Uц) = 0,3; Вероятность обнаружения сигнала от цели: Р(Uc/Uц) = 0,9; Вероятность появления ложного сигнала от помех: Р(Uc/Uп) = 0,05. Вычислив функцию правдоподобия, определить, есть в принятой реализации сигнал или его нет.
По каналу связи, подверженному воздействию помех, передается одна из команд управления в виде кодовых комбинаций 11111 или 00000, причем априорные вероятности передачи этих команд соответственно равны 0,6 и 0,4. Из-за наличия помех вероятность правильного приема каждого из символов (1 и 0) уменьшается до 0,5. Предполагается, что символы кодовых комбинаций искажаются независимо друг от друга. На выходе приемного устройства зарегистрирована комбинация 10110. Определить какая команда была передана (11111 или 00000).
Каждая буква «АКВААЭРОБИКА» написана на отдельной карточке, карточки тщательно перемешаны. Последовательно извлекаются пять карточек.
Какова вероятность Р(А) получить слово «БАРАК»?
Случайная величина Х треугольного вида (рис.1) имеет плотность вероятности, которую можно представить выражением:
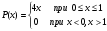
Определить математическое ожидание, дисперсию и среднее квадратическое отклонение случайно величины Х.
Два из трех независимо работающих элементов вычислительного устройства отказали.
Вычислить вероятность того, что отказали первый и второй элементы, если вероятности отказа первого, первого и третьего элементов соответственно равны 0,4; 0,2; 0,3.
В студии имеются четыре телевизионных камеры. Вероятность того, что каждая камера работает в данный момент времени, равна 0,65.
Найти вероятность того, что в данный момент времени включена хотя бы одна камера.
Система управления состоит из четырех узлов В1, В2 ,В3 и В4 (рис. 4). Вероятность рi безотказной работы узлов соответственно равны р1, р2, р3 и р4.
Вычислить вероятность безотказной работы Р всей системы управления
В1
В2
В3
В4
Рис. 4 |
 Скачать 50.06 Kb.
Скачать 50.06 Kb.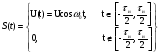
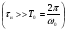 . Найти энергию радиоимпульса и сравнить её с энергией видеоимпульса. Привести спектры видео и радиоимпульса.
. Найти энергию радиоимпульса и сравнить её с энергией видеоимпульса. Привести спектры видео и радиоимпульса.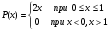
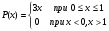
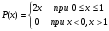
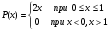
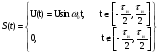
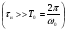 . Найти энергию радиоимпульса и сравнить её с энергией видеоимпульса. Привести спектры видео и радиоимпульса.
. Найти энергию радиоимпульса и сравнить её с энергией видеоимпульса. Привести спектры видео и радиоимпульса.