Задание Найти частные производные функции Находим частные производные
 Скачать 29.56 Kb. Скачать 29.56 Kb.
|
|
Задание 1. Найти частные производные функции 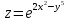 Находим частные производные: При нахождении 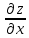 считаем аргумент считаем аргумент 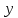 постоянным: постоянным: 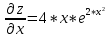 При нахождении 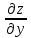 считаем аргумент считаем аргумент 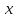 постоянным: постоянным: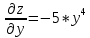 Найдем смешанные частные производные: Для того, чтобы найти 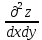 дифференцируем дифференцируем 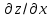 по по 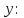 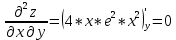 Задание 2. Найти частные производные второго порядка функции 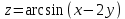 Убедиться в том, что 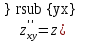 Находим частные производные: При нахождении 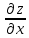 считаем аргумент считаем аргумент 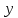 постоянным: постоянным: 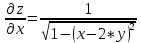 При нахождении 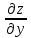 считаем аргумент считаем аргумент 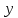 постоянным: постоянным: 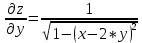 Полный дифференциал функции: 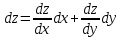 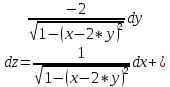 Находим вторые частные производные: 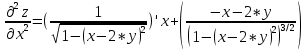 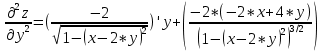 Найдем смешанные частные производные: Для того, чтобы найти 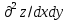 дифференцируем дифференцируем 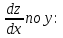 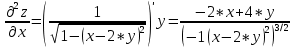 Задание 3. Дана функция 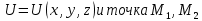 . Вычислить: производную этой функции в точке . Вычислить: производную этой функции в точке 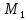 по направлению вектора: по направлению вектора: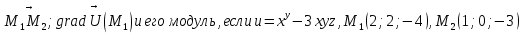 Градиентом функции 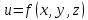 называется вектор, координатами которого являются частные производные данной функции, т.е.: называется вектор, координатами которого являются частные производные данной функции, т.е.: 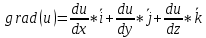 Находим частные производные: 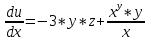 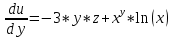 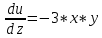 Тогда величина градиента равна: 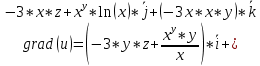 Найдем градиент в точке А (2;2;4) 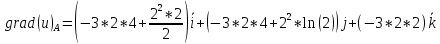 или 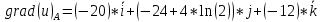 Модуль grad(u) – наибольшая скорость возрастания функции: 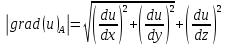 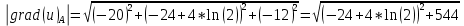 Направление вектора-градиента задается его направляющими косинусами: 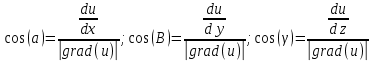 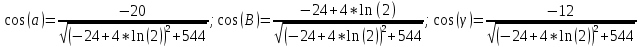 Найдем производную в точке А по направлению вектора а (-1; -2;1) 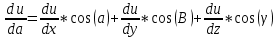 Найти направление вектора – значит найти его направляющие косинусы: 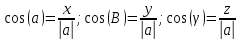 Модуль вектора 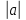 равен: равен: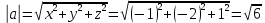 тогда направляющие косинусы: 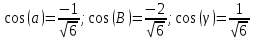 Для вектора а имеем: 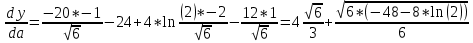 Если 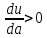 , то заданная функция в направлении вектора а возрастает. , то заданная функция в направлении вектора а возрастает. Если 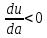 , то заданная функция в направлении вектора а убывает. , то заданная функция в направлении вектора а убывает. Задание 4. Дано уравнение 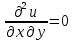 . Проверить, удовлетворяет ли данному уравнению функция . Проверить, удовлетворяет ли данному уравнению функция 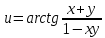 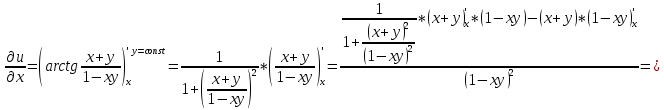 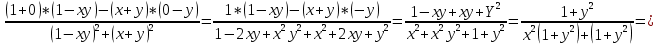 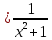 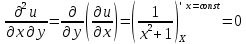 значит, функция 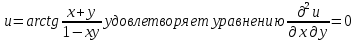 Задание 5. Найти наибольшее и наименьшее значения функции 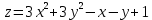 в области в области 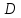 , ограниченной линиями , ограниченной линиями 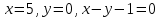 1)Построим область 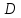 ограниченную линиями: ограниченную линиями: 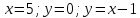 2) 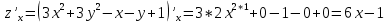 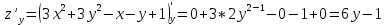 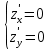 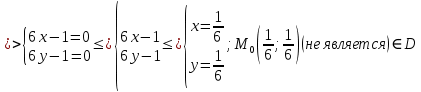 3) Исследуем границы области 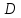 а) нижняя сторона треугольника ( 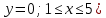 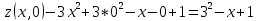 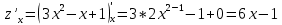 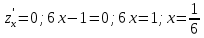 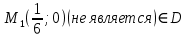 Исследуем концы отрезка точки 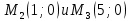 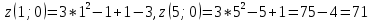 б) правая сторона треугольника 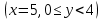 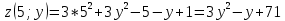 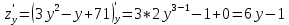 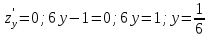 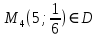 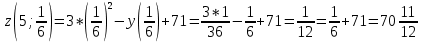 исследуем второй конец отрезка – точку 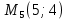 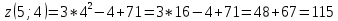 в) верхняя сторона треугольника 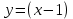 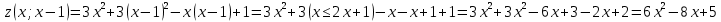 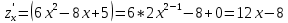 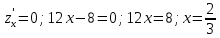 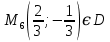 Концы отрезка уже исследованы 4) Имеем 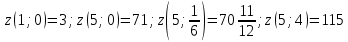 значит, 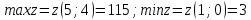 Задание 6. Вычислить интеграл 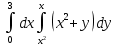 Сначала вычисляем внутренний интеграл: 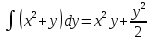 Подставляем пределы интегрирования 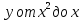 : :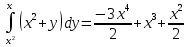 Потом вычисляем внешний интеграл: 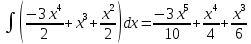 Подставляем пределы интегрирования x от 0 до 3: 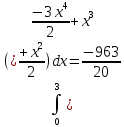 Задание 7. Вычислить интеграл 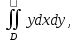 если если 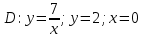 Сначала вычисляем внутренний неопределенный интеграл: 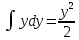 Подставляем пределы интегрирования y от 2 до 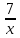 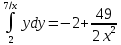 Потом вычисляем внешний интеграл: 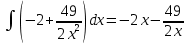 Подставляем пределы интегрирования х от 0 до 1: 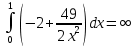 Задание 8. Вычислить интеграл 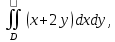 если если 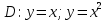 Сначала вычисляем внутренний неопределенный интеграл: 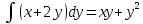 Подставляем пределы интегрирования 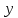 от от 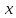 до до 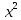 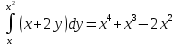 Потом вычисляем внешний интеграл: 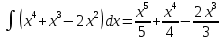 Подставляем пределы интегрирования х от 0 до 1: 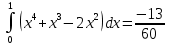 Задание 9. Вычислить интеграл 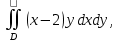 если если 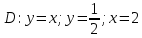 Сначала вычисляем внутренний неопределённый интеграл: 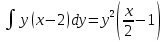 Подставляем пределы интегрирования y от х до 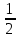 : :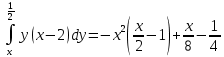 Потом вычисляем внешний интеграл: 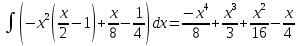 Подставляем пределы интегрирования х от 0 до 2 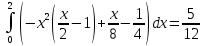 |
