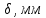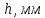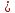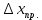Лабораторная работа. Лабораторная работа № 1. Задание Общая схема установки Рисунок Схематическое изображение цилиндра, где
 Скачать 159.62 Kb. Скачать 159.62 Kb.
|
|
Вариант 3 Цель работы: Исходя из заданных величин измерений, научиться обрабатывать данные. Вычислять погрешности прямых и косвенных измерений. Строить графики. Задание 1. Общая схема установки: 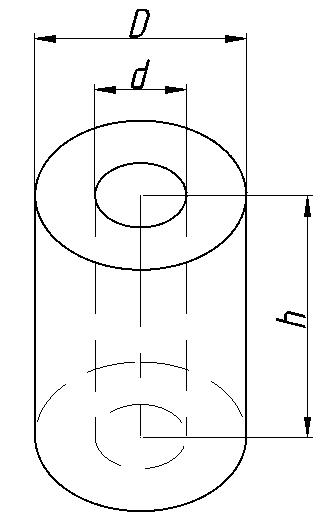 Рисунок 1. Схематическое изображение цилиндра, где: h – высота цилиндра; d – внутренний диаметр; D – внешний диаметр. Используемое оборудование: Штангенциркуль 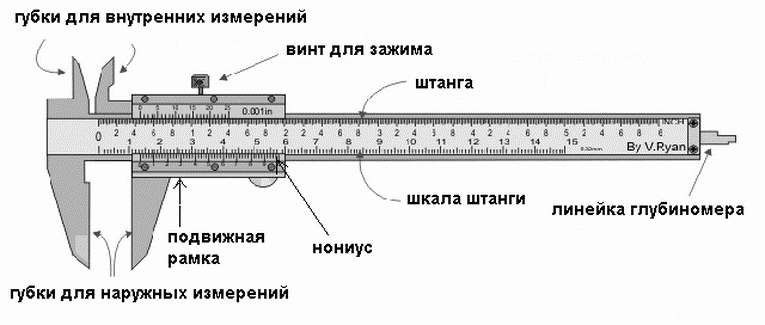 Рисунок 1. Штангенциркуль Данные приборов необходимых для вычисления погрешностей: Таблица 1. Измерительные приборы
Рабочие формулы: 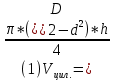 , , где 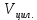 – объем цилиндра, – объем цилиндра,d - среднее значение внутреннего диаметра цилиндра, D - среднее значение внешнего диаметра цилиндра, π – const; 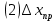 = =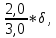 где 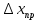 - абсолютная погрешность прибора, - абсолютная погрешность прибора,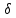 - максимальное значение погрешности прибора; - максимальное значение погрешности прибора;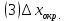 = = 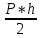 , , где 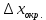 – абсолютная погрешность округления, – абсолютная погрешность округления,h – цена деления прибора (штангенциркуль = 0,05), P – доверительная вероятность (P=0,95); 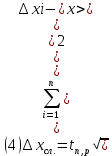 , , где 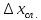 – случайная погрешность измерений, – случайная погрешность измерений,n – количество опытов, 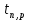 – коэффициент Стьюдента, – коэффициент Стьюдента, n – количество измерений, 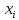 – измерение i-того порядка, – измерение i-того порядка,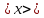 - среднее значение измерения; - среднее значение измерения;(5) 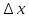 = =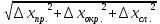 , , где 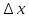 – полная абсолютная погрешность измерений, – полная абсолютная погрешность измерений,(6) 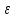 = =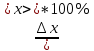 , , где 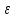 – относительная полная погрешность прямого измерения; – относительная полная погрешность прямого измерения;(7) 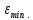 = =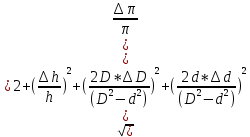 , ,где 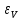 – минимальная погрешность, – минимальная погрешность,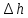 - абсолютная погрешность прямого измерения высоты, - абсолютная погрешность прямого измерения высоты,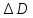 - абсолютная погрешность прямого измерения внешнего диаметра цилиндра, - абсолютная погрешность прямого измерения внешнего диаметра цилиндра,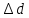 - абсолютная погрешность прямого измерения внутреннего диаметра цилиндра. - абсолютная погрешность прямого измерения внутреннего диаметра цилиндра.Основные результаты измерений: Таблица 2. Контрольные измерения цилиндра
Расчёт объёма цилиндра: 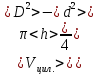 = 5121,900 = 5121,900 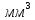 Расчёты искомых величин: (1) 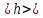 = =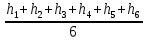 = =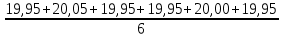 = 19,975; = 19,975;(2) 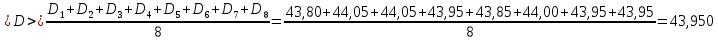 ; ;(3) 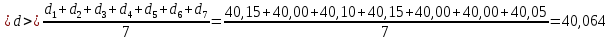 ; ;Расчёты погрешностей: 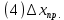 = =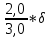 = = 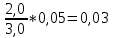 мм; мм;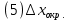 = =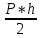 = =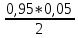 = 0,02 мм; = 0,02 мм;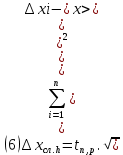 = 0,044; = 0,044;(7) 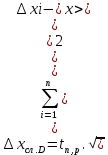 = 0,074; = 0,074;(8) 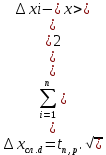 = 0,064; = 0,064;(9) 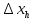 = =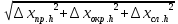 = 0,06; = 0,06;(10) 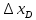 = =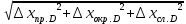 = 0,08; = 0,08;(11) 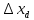 = = 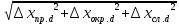 = 0,08; = 0,08;(12) 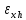 = =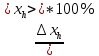 = =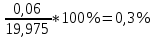 ; ;(13) 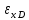 = = 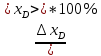 = = 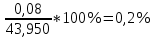 ; ;(14) 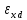 = =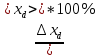 = = 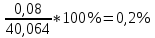 ; ;(15) 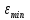 = =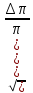 * 100% = 2,4%. * 100% = 2,4%.Окончательный результат измерений: 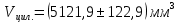 ; ; 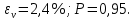 Вывод: Изучили методику обработки результатов прямых и косвенных измерений. Рассчитали, основываясь на представленные данные, объём и погрешности (случайную, приборную и округления) измерений. Задание 2. y = ax + b Рабочие формулы: (1) a = 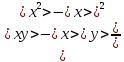 , ,где a – коэффициент функции y = ax + b; (2) b = 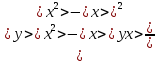 , ,где b – коэффициент функции y = ax + b; (3) 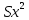 = = 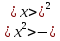 , ,где 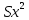 – дисперсия по x; – дисперсия по x;(4) 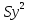 = =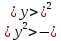 , ,где 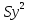 – дисперсия по y; – дисперсия по y;(5) 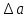 = =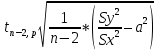 , ,где 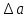 – погрешность коэффициента a, – погрешность коэффициента a,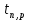 – коэффициент Стьюдента; – коэффициент Стьюдента; (6) 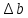 = =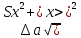 , ,где 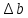 – погрешность коэффициента b; – погрешность коэффициента b;(7) 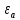 = =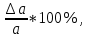 где 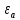 – относительная погрешность коэффициента a; – относительная погрешность коэффициента a;(8) 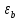 = =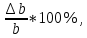 где 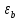 – относительная погрешность коэффициента b; – относительная погрешность коэффициента b;(9) 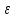 = =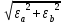 , ,где 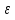 – относительная погрешность коэффициентов a и b. – относительная погрешность коэффициентов a и b.Основные результаты измерений: Таблица 3. Результаты измерений
Расчеты искомых величин: (1) a = 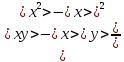 = 4,429; = 4,429;(2) b = 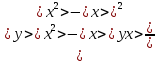 = 7,843; = 7,843;(3) 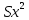 = = 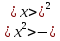 = 8,250; = 8,250;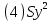 = = 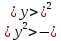 = 164,127; = 164,127;(5) 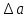 = =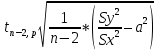 = 0,4322; = 0,4322;(6) 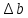 = = 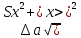 = 6,38. = 6,38.Расчёты погрешностей: (1) 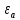 = =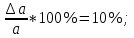 (2) 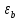 = =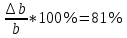 ; ;(3) 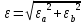 = 82%. = 82%.График: y = ax + b 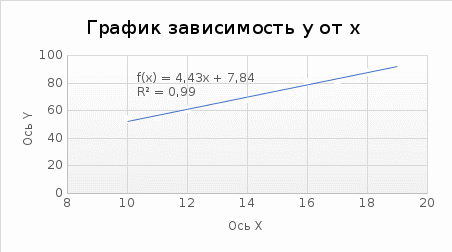 Окончательный результат измерений: 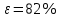 ; ; 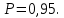 Вывод: На основании данных величин (x и y) и зависимости y от x, были выполнены расчеты погрешностей по методу наименьших квадратов и построен график данной зависимости. Согласно расчётам, относительная погрешность коэффициентов равна 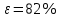 . .Задание 3. Рабочие формулы: (1) a = 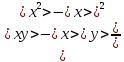 , ,где a – коэффициент линейной функции y = ax + b; (2) b = 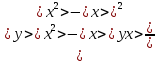 , ,где b – коэффициент линейной функции y = ax + b; (3) 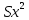 = =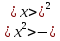 , ,где 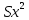 – дисперсия по x; – дисперсия по x;(4) 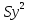 = = 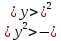 ; ;где 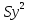 – дисперсия по y; – дисперсия по y;(5) 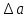 = =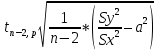 , ,где 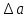 – погрешность коэффициента a, – погрешность коэффициента a,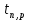 – коэффициент Стьюдента; – коэффициент Стьюдента; (6) 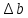 = = 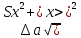 , ,где 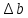 – погрешность коэффициента b; – погрешность коэффициента b;(7) y = C 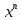 , ,где C – коэффициент степенной функции y = C 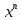 ; ;(8) lny = lnC+n*lnx; (9) Y = b+aX, где Y = lny, b = lnC, a = n, n – коэффициент степенной функции y = C 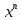 , , X = lnx; (10) C = exp(b) = 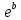 , ,где C – коэффициент степенной функции y = C 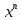 , ,е – const, равная 2,71828… (11) 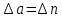 , ,где 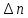 – погрешность коэффициента n; – погрешность коэффициента n;(12) 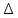 C = C =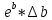 , ,где 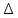 C – погрешность коэффициента C, C – погрешность коэффициента C,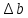 – погрешность коэффициента b; – погрешность коэффициента b; (13) 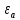 = =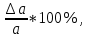 где 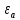 – относительная погрешность коэффициента a; – относительная погрешность коэффициента a;(14) 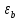 = = 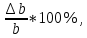 где 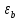 – относительная погрешность коэффициента b; – относительная погрешность коэффициента b;(15) 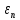 = =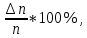 где 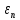 – относительная погрешность коэффициента n; – относительная погрешность коэффициента n;(16) 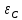 = =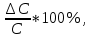 где 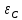 – относительная погрешность коэффициента C; – относительная погрешность коэффициента C;(17) 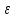 = = 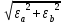 , ,где 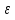 – относительная погрешность коэффициентов линейной функции; – относительная погрешность коэффициентов линейной функции;(18) 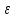 = = 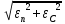 , ,где 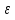 – относительная погрешность коэффициентов степенной функции. – относительная погрешность коэффициентов степенной функции.Основные результаты измерений: Таблица 4. Результаты измерений
Расчёты искомых величин: (1) a = 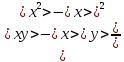 = -0,99; = -0,99;(2) b = 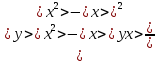 = 1,02; = 1,02;(3) 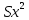 = = 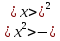 = 0,48; = 0,48;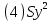 = =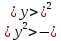 = 0,90; = 0,90;(5) 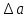 = =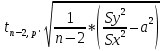 = 0,16; = 0,16;(6) 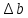 = = 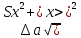 = 0,10; = 0,10;(7) 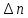 = 0,16; = 0,16;(8) C = 2,7734; (9) 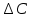 = 0,30. = 0,30.Расчёты погрешностей: (1) 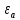 = = 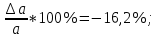 (2) 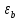 = = 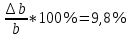 ; ;(3) 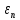 = = 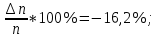 (4) 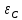 = = 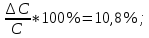 (5) 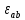 = = 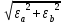 = 18,9%; = 18,9%;(6) 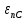 = = 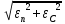 = 19,5%. = 19,5%.График: y = C 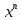 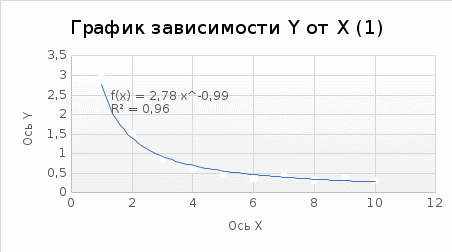 Y = aX + b 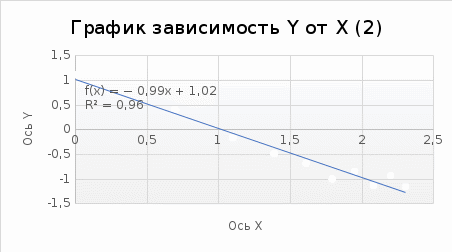 Окончательные результаты измерений: 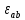 = 18,9%; = 18,9%;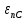 = 19,5%; = 19,5%; 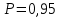 . .Вывод: Был использован метод наименьших квадратов для нелинейной зависимости. Исходное уравнение было преобразовано в линейное, так же были подсчитаны погрешности данных зависимостей. Относительная погрешность коэффициентов функций не превысила 19,5%. |