УправлениеИт проектами. Приложение 2. Задание Проект представлен сетевым графиком (рис. 1). Известны следующие значения параметров

• Название: Задание Проект представлен сетевым графиком (рис. 1). Известны следующие значения параметров
• Анкор: УправлениеИт проектами
• Дата: 26.05.2022
• Размер: 28.65 Kb.
• Имя файла: Приложение 2.docx
• Тип: Решение; #551490

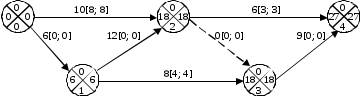Рис. 1. Исходный сетевой график к задачам 1, 2


Задание 1. Проект представлен сетевым графиком (рис. 1).

Известны следующие значения параметров:

срок выполнения проекта t₀=25 (для исходных данных t_кр= 27);

минимально возможное время выполнения работ d₀₁=5, d₀₂=6, d₁₂=7, d₁₃=5, d₂₄=4, d₃₄=8;

технологические коэффициенты использования дополнительных средств k₀₁=0,15, k₀₂=0,25, k₁₂=0,15, k₁₃=0,35, k₂₄=0,12, k₃₄=0,35.

Требуется найти такие t_pj,t_ij, x_ij, чтобы

• 
  суммарное количество используемых дополнительных средств было минимальным;
  
• 
  время выполнения всего комплекса работ не превосходило t₀;
  
• 
  продолжительность выполнения каждой работы была не меньше заданного значения параметра d_ij.
  

Решение

F(x) =x₀₁+ x₀₂+x₁₂+x₁₃+x₂₄+x₃₄ (min). (7)

Условия (2), ограничивающие время выполнения проекта 25 ед. времени, запишутся в виде:

t_p4  25. (8)

Условия (3), требующие выполнения каждой работы за время не меньше минимально возможного времени, выразятся так:
t₀₁5; t₀₂6; t₁₂7; t₁₃5; t₂₄4; t₃₄8. (9)

Зависимости (4) продолжительности работ от вложенных в них средств принимают следующий вид:
t₀₁=6– 0,15x₀₁; t₀₂=10 – 0,25x₀₂;(9) t₁₂=12 – 0,15x₁₂(20); t₁₃=8 – 0,35x₁₃;

t₂₄=6–0,12x₂₄;(7) t₃₄=9 – 0,35x₃₄.(20) (10)
Требования (5) своевременной выполняемости всех предшествующих работ обеспечиваются при следующих условиях:
t_p4 t_p2 + t₂₄; t_p4 t_p3 + t₃₄; t_p3 t_p2 + t₂₃; t_p3 t_p1 + t₁₃;

t_p2  t_p0 + t₀₂; t_p2  t_p1 + t₁₂; t_p1  t_p0 + t₀₁. (11)
Требования (6) – определяемые значения переменных должны быть неотрицательными:
t_p0 0; t_p1 0; t_p2  0; t_p3  0; t_p4  0;

t₀₁0; t₀₂0; t₁₂0; t₁₃0; t₂₃=0; t₂₄0; t₃₄0.

x₀₁0, x₀₂0, x₁₂0, x₁₃0, x₂₄0, x₃₄0. (12)
После решения данной задачи симплексным методом получены следующие результаты:
t_p0 =0; t_p1 =6; t_p2 = 15; t_p3 = 15; t_p4 = 22;

t₀₁=6; t₀₂=10; t₁₂=9; t₁₃=8; t₂₃=0; t₂₄=6; t₃₄=7.

x₀₁=0, x₀₂=0, x₁₂=30, x₁₃=0, x₂₄=0, x₃₄=4.

F(x)_min =34.
Таким образом, чтобы выполнить проект за время t₀=22, необходимо дополнительно вложить 34 ед. средств. В этом случае средства должны быть распределены следующим образом: 30 ед. в работу (1, 2) и 4 ед. в работу (3, 4), что приведет к сокращению времени выполнения этих работ.
Задание 2. Проект представлен сетевым графиком (рис. 1).

Известны следующие значения параметров: максимальная величина дополнительных средств, которая может быть выделена на реализацию проекта составляет В=45 ед. средств; минимально возможное время выполнения работ d₀₁=5, d₀₂=6, d₁₂=7, d₁₃=5, d₂₄=4, d₃₄=8; технологические коэффициенты использования дополнительных средств k₀₁=0,15, k₀₂=0,25, k₁₂=0,15, k₁₃=0,35, k₂₄=0,12, k₃₄=0,35.

Требуется найти такие t_pj,t_ij, x_ij, чтобы

• 
  суммарное количество используемых дополнительных средств было не более значения параметра В;
  
• 
  время выполнения всего комплекса работ было минимальным;
  
• 
  продолжительность выполнения каждой работы была не меньше заданного значения параметра d_ij.
  

F(x) =x₀₁+ x₀₂+x₁₂+x₁₃+x₂₄+x₃₄ (min). (7)

Условия (2), ограничивающие время выполнения проекта 22 ед. времени, запишутся в виде:

t_p4  22. (8)

Условия (3), требующие выполнения каждой работы за время не меньше минимально возможного времени, выразятся так:
t₀₁4; t₀₂6; t₁₂5; t₁₃4; t₂₄3; t₃₄7. (9)
Зависимости (4) продолжительности работ от вложенных в них средств принимают следующий вид:
t₀₁=6– 0,1x₀₁; t₀₂=10 – 0,5x₀₂; t₁₂=12 – 0,1x₁₂; t₁₃=8 – 0,3x₁₃;

t₂₄=6–0,2x₂₄; t₃₄=9 – 0,5x₃₄. (10)
Требования (5) своевременной выполняемости всех предшествующих работ обеспечиваются при следующих условиях:
t_p4 t_p2 + t₂₄; t_p4 t_p3 + t₃₄; t_p3 t_p2 + t₂₃; t_p3 t_p1 + t₁₃;

t_p2  t_p0 + t₀₂; t_p2  t_p1 + t₁₂; t_p1  t_p0 + t₀₁. (11)
Требования (6) – определяемые значения переменных должны быть неотрицательными:
t_p0 0; t_p1 0; t_p2  0; t_p3  0; t_p4  0;

t₀₁0; t₀₂0; t₁₂0; t₁₃0; t₂₃=0; t₂₄0; t₃₄0.

x₀₁0, x₀₂0, x₁₂0, x₁₃0, x₂₄0, x₃₄0. (12)
После решения данной задачи симплексным методом получены следующие результаты:
t_p0 =0; t_p1 =6; t_p2 = 15; t_p3 = 15; t_p4 = 22;

t₀₁=6; t₀₂=10; t₁₂=9; t₁₃=8; t₂₃=0; t₂₄=6; t₃₄=7.

x₀₁=0, x₀₂=0, x₁₂=30, x₁₃=0, x₂₄=0, x₃₄=4.

F(x)_min =34.