Итоговая работа 2101-0400-2102067 Соболева И.А.. Задание Решить систему линейных алгебраических уравнений
 Скачать 51.62 Kb. Скачать 51.62 Kb.
|
Практическое задание
дисциплине
Пермь 2022 Задание 1. Решить систему линейных алгебраических уравнений. 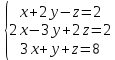 Решение: Решение проведём методом Гаусса. Для этого записываем систему в виде расширенной матрицы: 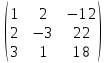 Далее вычитаем из строки 2 строку 1 умноженную на –2, чтобы получить нули ниже ведущего элемента: 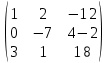 Вычитаем из строки 3 строку 1 умноженную на –3, чтобы получить нули ниже ведущего элемента: 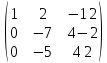 Вычитаем из строки 3 строку 2 умноженную на – 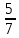 , чтобы получить нули ниже ведущего элемента: , чтобы получить нули ниже ведущего элемента: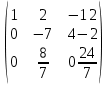 => => 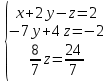 Из последнего уравнения 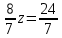 находим, что z=3. Подставляем это значение во второе уравнение: находим, что z=3. Подставляем это значение во второе уравнение:–7y + 4 × 3 = –2 –7y = –2 – 12 –7y = –14 y = 2 В первое уравнение поставляем y и z: X + 2 × 2 = 2 X = 2 – 1 X = 1 Ответ: X = 1 ; y = 2 ; z = 3. Задание 2. Дано z1 = 5 – 4i и z2 = –1 – i. Выполнить действия: А) z1+ z2; Б) z1 × z2; В) z1 / z2. Решение: z1+ z2 = 5 – 4i – 1 – i = 4 – 5i. z1 × z2 = (5 – 4i) ×( – 1– i) = – 5 – 5i + 4i + 4 = – 9 – i. 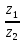 = = 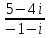 = = 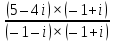 = = 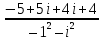 = = 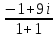 = – = – 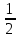 + + 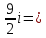 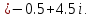 Ответ: а) 4 – 5i; б) – 9 – i; в) 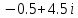 . . Задание 3.Найти математическое ожидание и дисперсию, заданной законом распределения:
Решение: M(X) = –5 × 0.4 + 2 × 0.3 + 3 × 0.1 + 4 × 0.2 = – 0.3. D(X) = M(X2) – ((M(X))2 M(X2) = –52 × 0.4 + 22 ×0.3 + 32 × 0.1 + 42 × 0.2 = 10+ 1.2 + 0.9 + 3.2 = 15.3. D(X) = 15.3 – 0.32 = 15.3 – 0.09 = 15.21. Ответ: M(X) = – 0.3; D(X) = 15.21. Задание 4. Вычислить предел 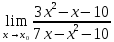 при x0=2. при x0=2.Решение: Применить теорему о пределе частного нельзя, так как при x=2 числитель и знаменатель обращаются в нуль. 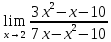 => => 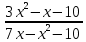 = = 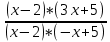 = = 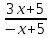 = = 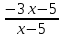 Переходим к пределу: 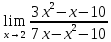 = = 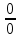 = = 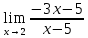 = = 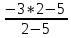 = = 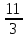 . .Ответ: предел при x0=2 : 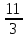 . .Задание 5. Найти производную функции y = 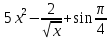 . .Решение: y = 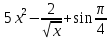 = = 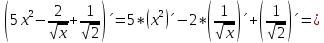 = 5 × 2x – 2 ×(– 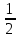 ) × ) × 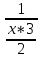 = 10x + = 10x + 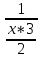 . . Ответ: 10x + 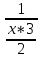 . .Задание 6. Вычислить неопределенный интеграл 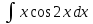 . .Решение: Пусть u = x, du = cos2xdx . Тогда u = 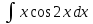 = = 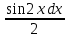 => =>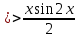 – –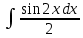 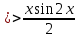 – – 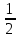 × × 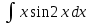 . .Заменяем t = 2x, а dt = 2dx => dx = 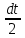 => =>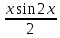 – – 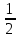 × ×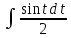  => => 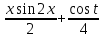 . (т.к. . (т.к. 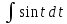 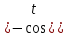 Обратная замена: 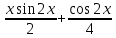 = x = x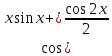 +C. +C.Ответ: x 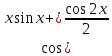 +C. +C. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
