2109.05.06 СурГУ ИТ обр_инф_1_курс_заочка_2018 (Практическая Вар. Задание Системы счисления, представление чисел с фиксированной запятой (ФЗ) и плавающей запятой (ПЗ) в разрядной сетке
 Скачать 479.8 Kb. Скачать 479.8 Kb.
|
Задание 1. Системы счисления, представление чисел с фиксированной запятой (ФЗ) и плавающей запятой (ПЗ) в разрядной сетке.Вариант 25 1.1 Преобразуйте числа (238)10=( )2 , (FC86)16=( )10, (1011111,0011)2=( )10, (745)8=( )10 , (258)10=( )8 , (2336)10=( )16 (238)10 = ( )2 Делим 238 последовательно на 2  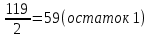       Записываем остатки деления в обратном порядке : (11101110)2 Ответ: (238)10 = (11101110)2 (FC86)16 = ( )10 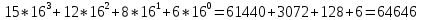 Ответ: (FC86)16 = (64646)10 (1011111,0011)2 = ( )10   Ответ: (1011111,0011)2=(  )10 )10(745)8=( )10  Ответ: (745)8 = (485)10 (258)10=( )8 Делим 258 последовательно на 8:    Записываем остатки деления в обратном порядке: (402)8 Ответ: (258)10=(402)8 (2336)10=( )16 Делим 2336 последовательно на 16:    Записываем остатки деления в обратном порядке: (920)16 Ответ: (2336)10=(920)16 1.2 Найдите значение выражения: (101101,1112) +(11011,101)2 Складываем в столбик: 101101,111+ 11011,101 (1  (1 (1 (1 (1 (1 (1 (1 (1 (1 (1 (1 (1 (1 (1 (1 (1 1 0 1 1 0 1, 1 1 1 + 1 1 0 1 1, 1 0 1 1 0 0 1 0 0 1, 1 0 0 Ответ: (101101,111)2 + (11011,101)2 = (1001001,100)2 Найдите значение выражения: (6046)8-(1777)8 Вычитаем в столбик: (6046)8-(1777)8 6-1-1=4 7-7=0 3+8-7=4 6+8-7=7 6 0 4 6 – 1 7 7 7 4 0 4 7 Ответ: (6046)8-(1777)8 = (4047)8 1.3 Представьте положительное целое число в формате с фиксированной запятой (ФЗ) (131)10 Переведём число в двоичную систему счисления: Делим 131 последовательно на 2         (131)10 = (10000011)2 Записываем число в формате кратном 1 байту: 1000 0011 Ответ: 0100 1100 1.4 Представьте целое число со знаком в формате с фиксированной запятой (ФЗ): (-157)10 Переведём число в двоичную систему счисления: Делим 157 последовательно на 2  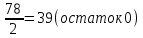       (157)10 = (10011101)2 Записываем число в формате кратном 2 байтам: 0000 0000 1001 1101 Полученное число переводим в обратный код: 1111 1111 0110 0010 К полученному коду прибавляем 1: 1111 1111 0110 0011 Ответ: 1111 1111 0110 0011 1.5 Представьте число в формате с плавающей запятой (ПЗ) обычной точности: (197)10 Переведём число в двоичную систему счисления: Делим 197 последовательно на 2  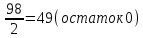     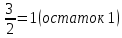  (197)10 = (11000101)2 (197)10 = 1.1000101e7 Порядок = 7. Мантисса = 1000101 Вычисляем порядок для записи в память: 127+7=134 Переведём число в двоичную систему счисления: Делим 134 последовательно на 2         (134)10 = (10000110)2
1.6 Представить число в формате с плавающей запятой (ПЗ) двойной точности: (-197)10 Переведём число в двоичную систему счисления. Воспользуемся результатом из примера 1.5 (197)10 = (11000101)2 Вычисляем порядок для записи в память: 1023+7=1030 Переведём число в двоичную систему счисления: Делим 1030 последовательно на 2  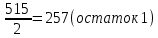  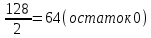        (1030)10 = (100 0000 0110)2 Записываем число на основе вычислений:
1.7 Вычислите выражение: (225)8+(10111)2+(F2)16-(577)8 Поскольку в задании не оговорена система счисления результата, приведём ответ в десятичном счислении. Переведём число (225)8 в десятичную систему счисления:  Переведём число (10111)2 в десятичную систему счисления: 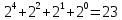 Переведём число (F2)16 в десятичную систему счисления: 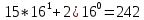 Переведём число (577)8 в десятичную систему счисления: 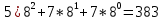 Полученную сумму записываем в десятичном счислении: 149 + 23 + 242 – 383 = 31 Ответ: (225)8+(10111)2+(F2)16-(577)8 = (31)10 Задание 2а. Обработка данных в Excel и создание отчета в Word 1. Ввести исходную матрицу (А): Вбили в девять ячеек экселя с A:1 по C:3 значения для своего варианта. В C4 установили произвольный множитель (его нет в задании). 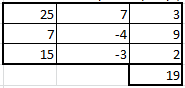 2. Умножение исходной матрицы на число (В=А*число) Выделили мышью 3х3 пустых ячейки, нажали "равно" на клавиатуре, выделили мышью 3х3 ячейки с введённой матрицей А, нажали на клавиатуре "*", кликнули по множителю в ячейке С4. Зажали на клавиатуре Shift, Ctrl и нажали Enter. Сформировалась матрица B.  3. Произведение матриц (С=А*В) Выделили мышью 3х3 пустых ячейки, ввели с клавиатуры "=мумнож(", выделили мышью 3х3 ячейки с матрицей А, зажали Ctrl, выделили мышью 3х3 ячейки с матрицей B, зажали на клавиатуре Shift, Ctrl и нажали Enter. Сформировалась матрица С. Все недостающие скобки и знаки Excel подставил сам.  4. Сумма двух матриц (D=А+В) Выделили мышью 3х3 пустых ячейки, нажали "равно" на клавиатуре, выделили мышью 3х3 ячейки с матрицей А, нажали "+", выделили мышью 3х3 ячейки с матрицей B, ввели, зажали на клавиатуре Shift, Ctrl и нажали Enter. Сформировалась матрица D.  5. Выполнить следующие действия с матрицами: E=2*D Выделили мышью 3х3 пустых ячейки, нажали "равно" на клавиатуре, выделили мышью 3х3 ячейки с матрицей D, ввели с клавиатуры "*2", зажали на клавиатуре Shift, Ctrl и нажали Enter. Сформировалась матрица E. 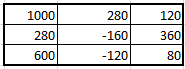 6. F=2*B-A Выделили мышью 3х3 пустых ячейки, нажали "равно" на клавиатуре, выделили мышью 3х3 ячейки с матрицей B, ввели с клавиатуры "*2-", выделили мышью 3х3 ячейки с матрицей A, зажали на клавиатуре Shift, Ctrl и нажали Enter. Сформировалась матрица F.  7. G=E*F Выделили мышью 3х3 пустых ячейки, ввели с клавиатуры "=мумнож(", выделили мышью 3х3 ячейки с матрицей E, зажали Ctrl, выделили мышью 3х3 ячейки с матрицей F, зажали на клавиатуре Shift, Ctrl и нажали Enter. Сформировалась матрица G.  8. H=A2 Выделили мышью 3х3 пустых ячейки, ввели с клавиатуры "=мумнож(", выделили мышью 3х3 ячейки с матрицей A, зажали Ctrl, снова выделили мышью 3х3 ячейки с матрицей A, зажали на клавиатуре Shift, Ctrl и нажали Enter. Сформировалась матрица H.  9. K=H+B Выделили мышью 3х3 пустых ячейки, нажали "равно" на клавиатуре, выделили мышью 3х3 ячейки с матрицей H, нажали "+", выделили мышью 3х3 ячейки с матрицей B, зажали на клавиатуре Shift, Ctrl и нажали Enter. Сформировалась матрица K. 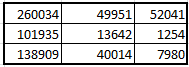 10. Найти произведение первого и второго столбцов матрицы А (L) Выделили мышью 1х3 пустых ячейки, нажали "равно" на клавиатуре, выделили мышью 1-й столбец матрицы А, нажали "+", выделили мышью 2-й столбец матрицы А, зажали на клавиатуре Shift, Ctrl и нажали Enter. Сформировалась матрица L. 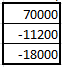 11. Умножить матрицу А на вектор - столбец (вектор - столбец сформировать самостоятельно) (M) Ввели столбец их 3 произвольных значений – это вектор-столбец. Выделили мышью 1х3 пустых ячейки, ввели с клавиатуры "=мумнож(" на клавиатуре, выделили мышью 3х3 ячейки с матрицей А, зажали Ctrl, выделили мышью вектор-столбец, зажали на клавиатуре Shift, Ctrl и нажали Enter. Сформировалась матрица M.  12. Найти определитель исходной матрицы А (N) Установили курсор в пустую ячейку, ввели с клавиатуры "=мопред(", выделили мышью 3х3 ячейки с матрицей A, зажали на клавиатуре Shift, Ctrl и нажали Enter. В ячейку поместился определитель матрицы A. 13. Транспонировать исходную матрицу А (P) Выделили мышью 3х3 пустых ячейки, ввели с клавиатуры "=трансп(", выделили мышью 3х3 ячейки с матрицей A, зажали на клавиатуре Shift, Ctrl и нажали Enter. Сформировалась матрица P.  14. Вычислить матрицу обратную к исходной матрице А (Q) Выделили мышью 3х3 пустых ячейки, ввели с клавиатуры "=трансп(", выделили мышью 3х3 ячейки с матрицей A, зажали на клавиатуре Shift, Ctrl и нажали Enter. Сформировалась матрица Q. 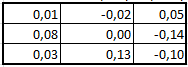 15. Доказать, что получена обратная матрица (т.е. получить единичную матрицу, перемножив исходную и обратную матрицу) (R) Выделили мышью 3х3 пустых ячейки, ввели с клавиатуры "=мумнож(", выделили мышью 3х3 ячейки с матрицей А, зажали Ctrl, выделили мышью 3х3 ячейки с матрицей Q, зажали на клавиатуре Shift, Ctrl и нажали Enter. Сформировалась матрица R, состоящая из нулей, с единицами по главной диагонали. 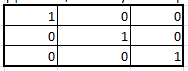 Данные в экселевском файле сгруппированы по уровням. Создание структуры невозможно по причине неоднородности данных (множитель в C4, определитель, вектор и т.п.). Задание 2а. Матричная алгебра в MS Excel. Техника построения графиков и гистограмм Задача 2.8 4. Построить гистограмму для следующих табличных данных (рис. 1.8). 5. Изменить на графике величину дохода в 2003 году. Какие изменения наблюдаются в таблице? 6. Внести изменения величины дохода в таблицу за 2002 год. Какие изменения наблюдаются в гистограмме? Результат выполнений пунктов два и три описать словесно, желательно сопроводить итоговыми гистограммами и таблицами. Гистограмма построена (к сожалению, описанный алгоритм создания не годится для Excel 2010, но ключевые детали соблюдены). Значение цветовой гаммы для 25-го варианта. Результат:  Меняем значение дохода за 2003-й год на 25:  Соответствующий столбец уменьшился, также изменилось значение. Меняем значение дохода за 2002-й год на 190. Шкала "Доход" увеличилась втрое, пропорционально увеличившемуся столбцу 2002:  Задача 2.9 Построить поверхность для нелинейной регрессии (производственная функция Кобба-Дугласа)  "Линии сетки – пунктир". К сожалению, данная опция в моем Excel 2010 недоступна, настраивается только цвет и толщина линий. Остальные требования соблюдены. Задача 2.10 Построить графики m = x2 - 2x -3, n = -2x + 1 на отрезке [-3;4] с шагом 0,5  Изменить график, потянув за маркер, нельзя – у маркера нет собственной позиции, которую можно изменить, координаты высчитываются, опираясь на таблицу с данными. Можно изменить линейную функцию на уровне формулы таблицы. Поменяются значения n в таблице, изменится вид графика: n = 3x – 7:  Меняем шрифты в значениях осей, меняем тип и цвет параболы и прямой на графике.  Задание 2в. Расчет графиков оплаты потребительского кредита различными способами1) Рассчитать график оплаты потребительского кредита дифференцированными платежами. Посчитать переплату банку. 2) Рассчитать график оплаты потребительского кредита аннуитентными платежами. Посчитать переплату банку. 3) Сравнить переплаты по каждому виду кредитования и сделать вывод, какой вид кредитования более выгодный и на сколько. Взят потребительский кредит в размере 650 000р. под 23,5% годовых на 2,5 года. По результатам расчётов: - при дифференцированном способе погашения переплата банку составит 196 942,88 р. за 2,5 лет. - при аннуитентном способе погашения переплата банку составит 215 693,14 р. за 2,5 лет. - разница в переплате между дифференцированном способе и аннуитентном составит 18 750,26 р. Дифференцированный способ выгоднее. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
