триггер. 15_1_1_Ок. Задание упростить логические выражения. Минимизировать логические выражения
 Скачать 184.49 Kb. Скачать 184.49 Kb.
|
|
ЗАДАНИЕ: 1. УПРОСТИТЬ ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ. 2. МИНИМИЗИРОВАТЬ ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ. 3. ПОСТРОИТЬ ДЛЯ ПОЛУЧЕННЫХ ВЫРАЖЕНИЙ ПЕРЕКЛЮЧАТЕЛЬНЫЕ СХЕМЫ Вариант № 15 1.  2.  3.  Схема состоит из трех параллельных ветвей Первая ветвь состоит из четырех переключателей a, b, c, d Описывается функцией  Упростим ее, используя законы алгебры логики: Распределительный  ; ;де Моргана 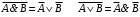  Составим схему переключателей рис. 1 Выключатели  и и 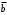 проводят ток, когда переключатель разомкнут, и не проводят, когда замкнут. Они включены последовательно, поэтому схема проводит ток, когда оба переключателя разомкнуты, и не проводит, когда один из них замкнут. К их соединению включен параллельно переключатель проводят ток, когда переключатель разомкнут, и не проводят, когда замкнут. Они включены последовательно, поэтому схема проводит ток, когда оба переключателя разомкнуты, и не проводит, когда один из них замкнут. К их соединению включен параллельно переключатель  . Переключатель . Переключатель 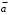 включен последовательно к соединению включен последовательно к соединению 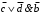 . .  Рис. 1 Вторая ветвь  Переключатели a, b, c включены последовательно, поэтому схема проводит ток, когда все переключатели замкнуты (рис. 2).  Рис. 2 Третья ветвь 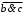 Преобразуем в соответствии с законом де Моргана   (рис. 3) включены параллельно, схема проводит ток, когда один из переключателей разомкнут (рис. 3) включены параллельно, схема проводит ток, когда один из переключателей разомкнут Рис. 3 2 Построим для полученных выражений переключательную схему Составим для минимизированной функции переключательную схему (рис. 4)   Рис. 4 Итоговая переключательная схема для  Задача 2  Решение: 1. Упрощение логических выражений Схема состоит из двух переключателей х1 и х2 Упростим ее используя законы алгебры логики: Распределительный  ; ;де Моргана 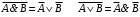 закон двойного отрицания   2 Построим для полученного выражений переключательную схему Составим для минимизированной функции переключательную схему (рис. 5). Схема состоит из трех параллельных ветвей. Первая ветвь состоит из 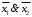 включённых последовательно переключателей включённых последовательно переключателей 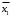 и и 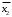 , вторая переключатель х1, третья переключатель х2 , вторая переключатель х1, третья переключатель х2  Рис. 5 Итоговая переключательная схема для  Задача 3  Решение: 1. Упрощение логических выражений Закон повторения  Исключения третьего  Операции с константами    |
