Реешение. Задание
 Скачать 184.5 Kb. Скачать 184.5 Kb.
|
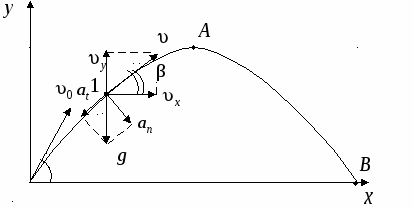
Задание.Тело массой 9 кг брошено под углом 79° к горизонту со скоростью 34 м/с. Определить tA время полёта тела до наивысшей точки траектории кинетическую энергию Wk и тангециальную составляющую ускорения тела Краткое теоретическое содержание 1) Явление, изучаемое в расчётно-графической работе: В данной расчетно-графической работе рассматривается движение тела под углом к горизонту. 2)Определение основных физических понятий, объектов: Движение тела, брошенного с некоторой начальной скоростью Vо под углом α к горизонту представляет собой сложное движение:равномерное по горизонтальному направлению и одновременно происходящее под действием силы тяжести равноускоренное движение в вертикальном направлении. Равномерное движение — механическое движение, при котором тело за любые равные отрезки времени проходит равные перемещения. Равномерное движение материальной точки — это движение, при котором скорость точки остаётся неизменной. Равноускоренное движение — движение, при котором ненулевой вектор ускорения остаётся неизменным по модулю и направлению. 3)Законы и соотношения, описывающие изучаемые процессы: В данной работе используются законы кинематики равномерного и равноускоренного движения. Равномерное движение: Скорость равномерного прямолинейного движения - это постоянная векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка. Перемещение: Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид: х = x0 + vt Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), тогда уравнение движения принимает вид: х = x0 – vt
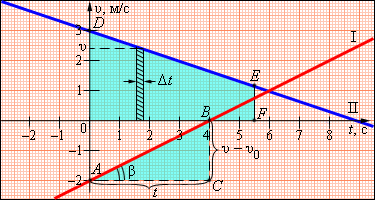
При равноускоренном прямолинейном движении скорость тела определяется формулой
В этой формуле υ0 – скорость тела при t = 0 (начальная скорость), a = const – ускорение. На графике скорости υ (t) эта зависимость имеет вид прямой линии (рис. 1.2).
По наклону графика скорости может быть определено ускорение a тела. Ускорение численно равно отношению сторон треугольника ABC:
Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна), тем больше ускорение тела. Например: Для графика I: υ0 = –2 м/с, a = 1/2 м/с2. Для графика II: υ0 = 3 м/с, a = –1/3 м/с2.
Так как υ – υ0 = at, то формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:
Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y0 прибавить перемещение за время t:
Это выражение называют законом равноускоренного движения. 4)Пояснения к физическим величинам, входящим в формулы, и единицы их измерения: Скорость - Перемещение — изменение местоположения физического тела в пространстве, относительно выбранной системы отсчёта. Измеряется в метрах (м). Сила — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Измеряется в Ньютонах (Н). Ускорение - Ускорение свободного падения g — ускорение, придаваемое телу в вакууме силой тяжести, В соответствии со вторым законом Ньютона, ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы. Значение ускорения свободного падения на поверхности Земли обычно принимают равным 9,8 или 10 м/с². Стандартное («нормальное») значение, принятое при построении систем единиц, g = 9,80665 м/с², а в технических расчётах обычно принимают g = 9,81 м/с². Траектория - это линия, вдоль которой движется тело (м). Путь - это сумма длин всех участков траектории, последовательно проходимых телом при движения (м). Решение
Рисунок 1 Для того что бы определить момент времени 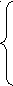 vx(t) = v0·cos(α); vу(t) = v0· sin(α) – g·t; При полёте вверх тело двигается равнозамедленно с ускорением –g. Время 0 = v0·sin(α) – g·tA, откуда Полная скорость тела Для любой точки полёта полное ускорение составляет : а = Зависимость тангециального ускорения at(t) тела от времени имеет вид: аn(t) = g· 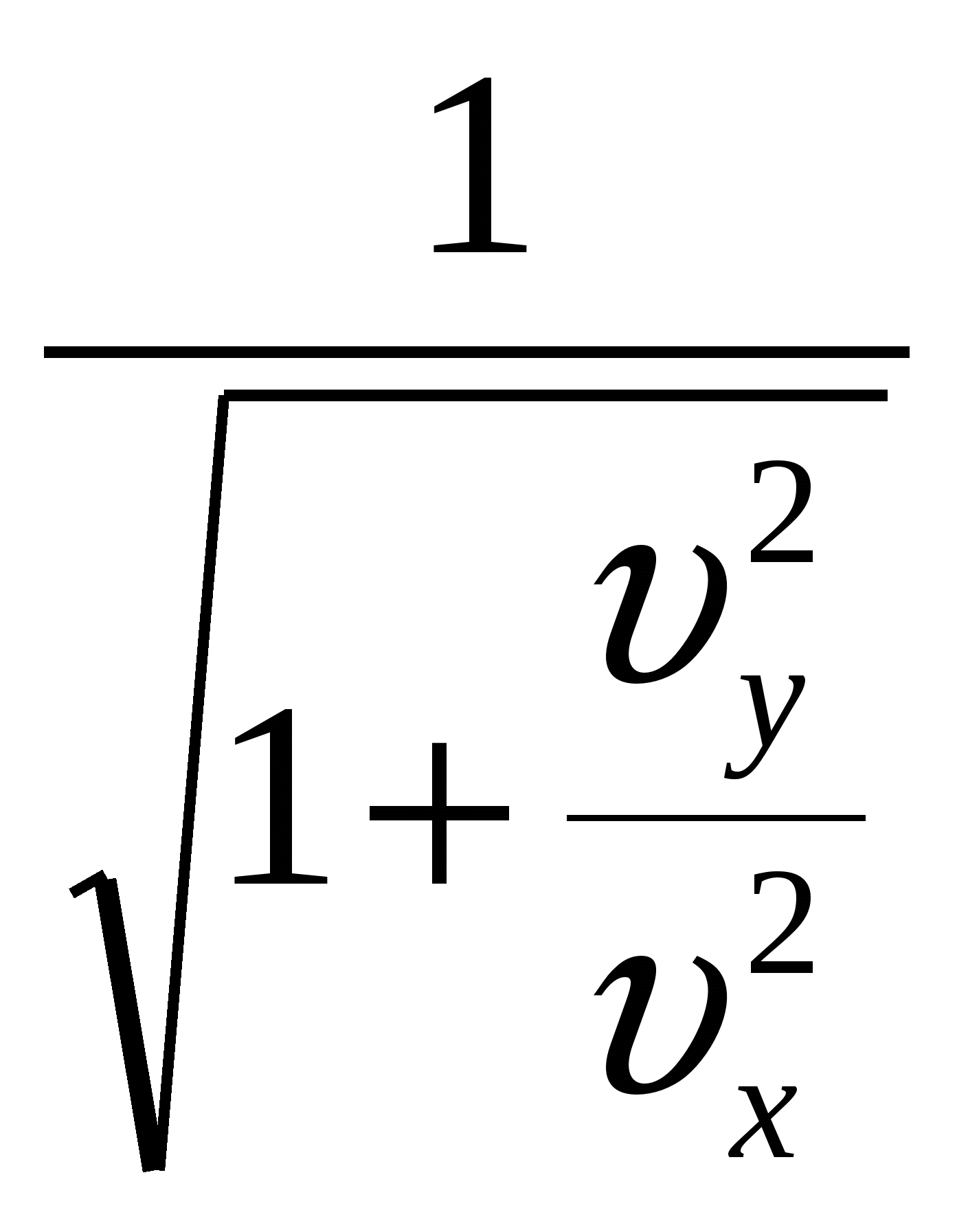 = g· = g·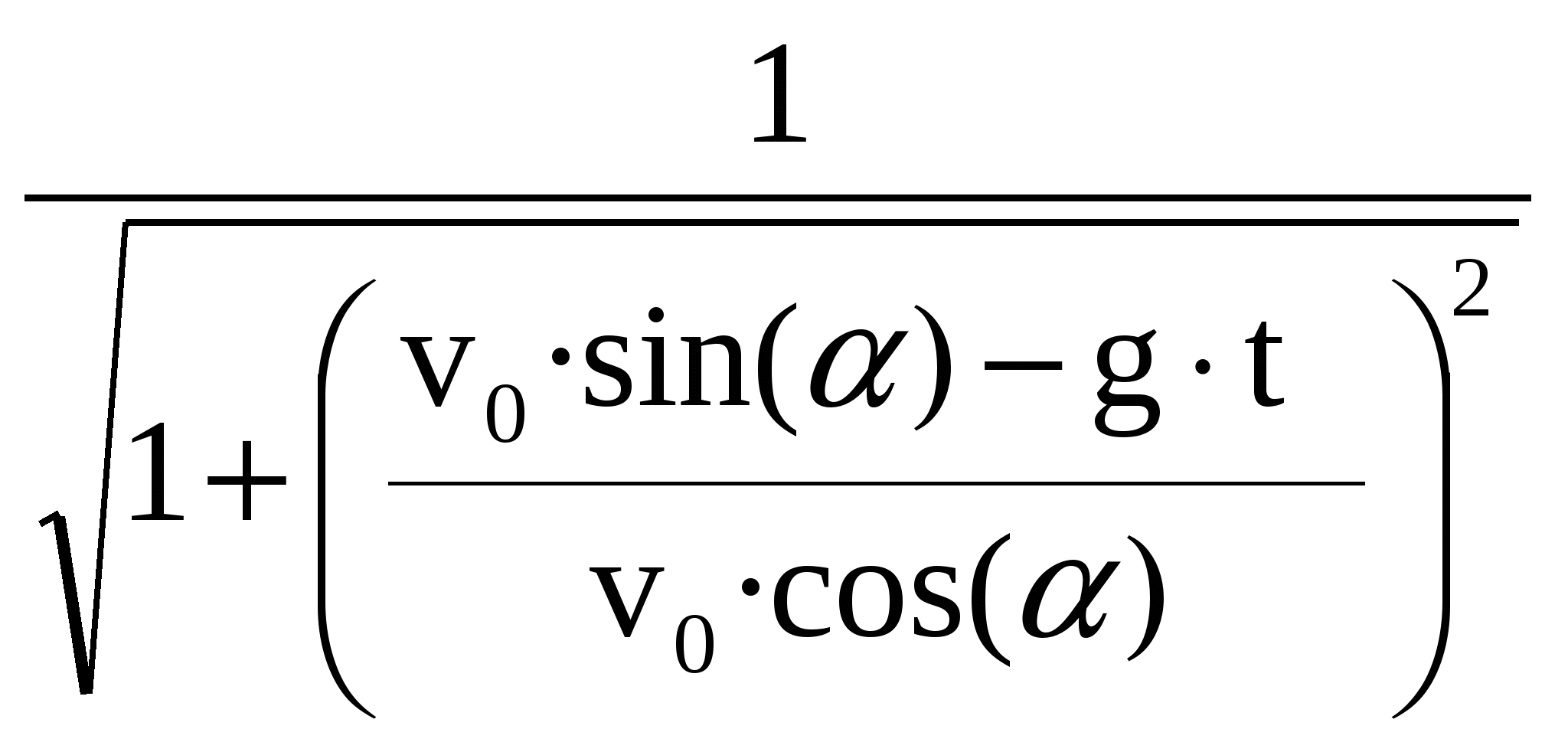 = =g· = =g· ; ;В момент времени аn(t1) = g· 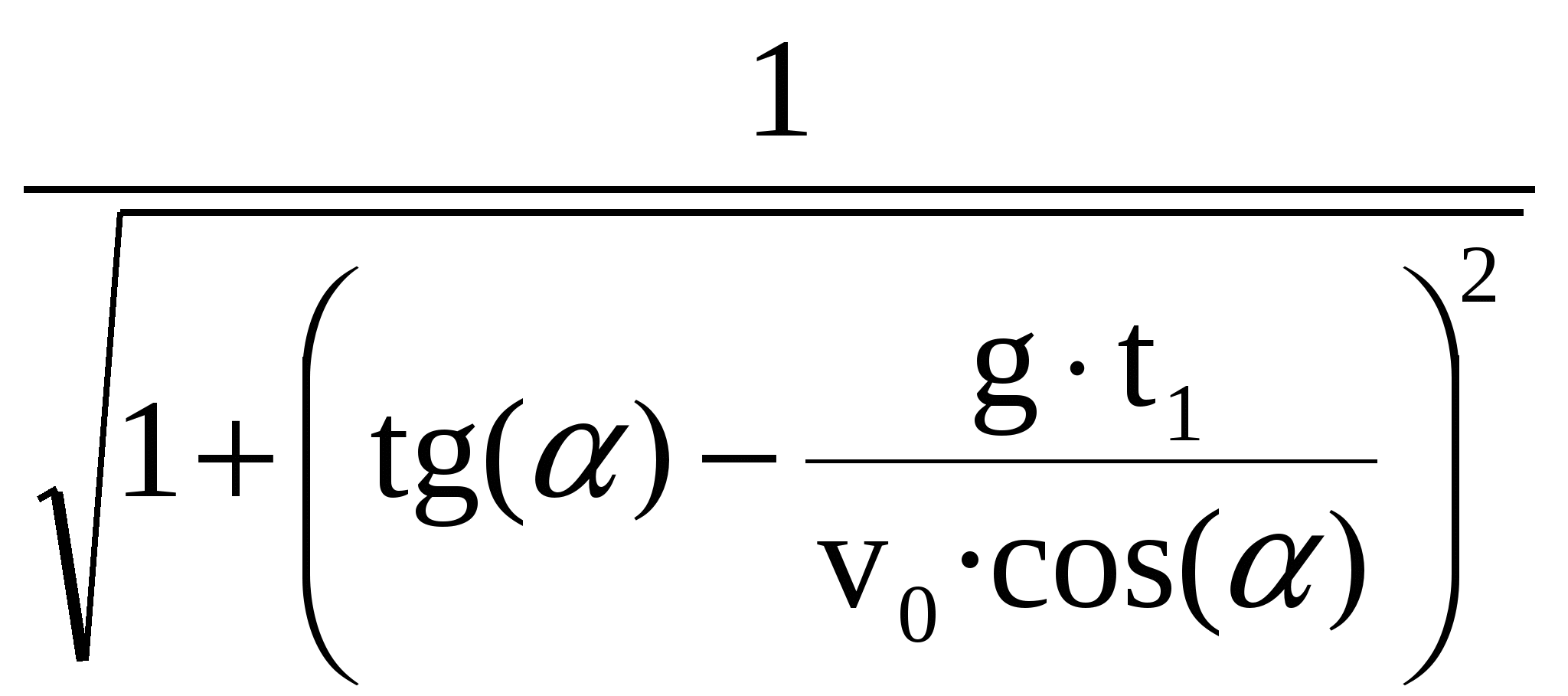 = 9,81· = 9,81·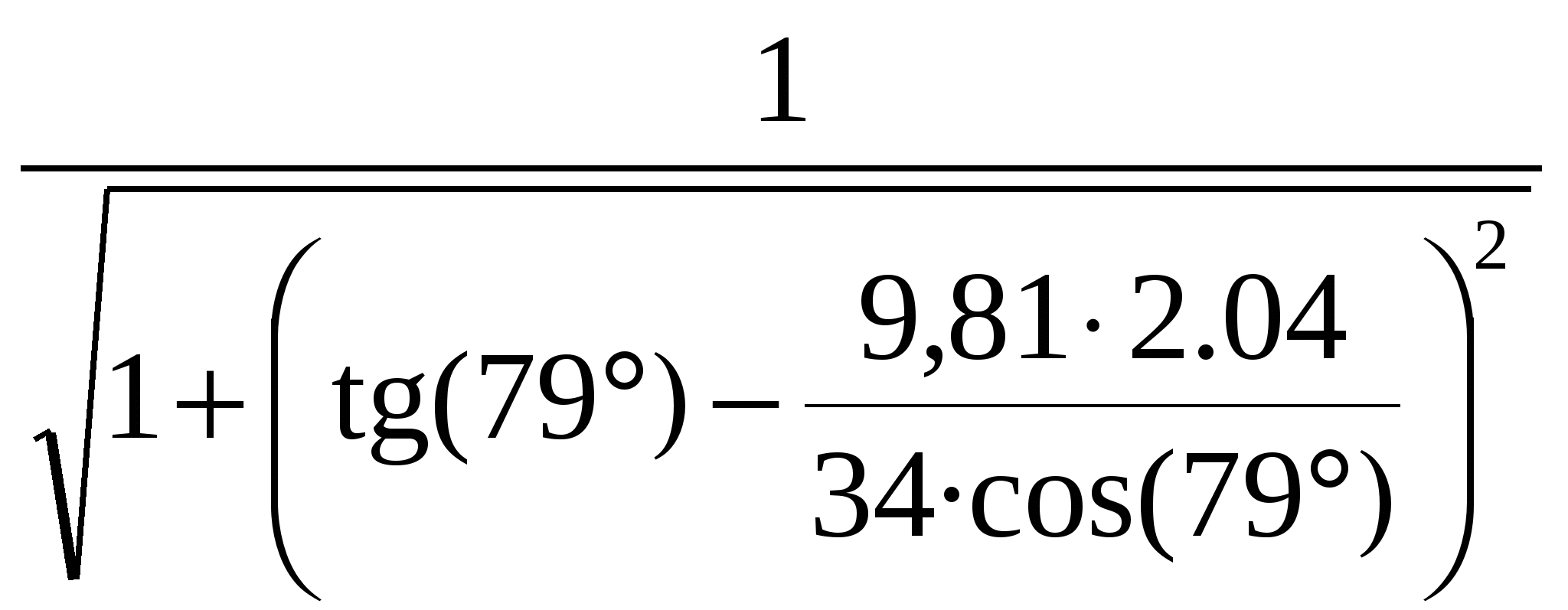 = 4,29 м/с2 = 4,29 м/с2Построим зависимость an(t) 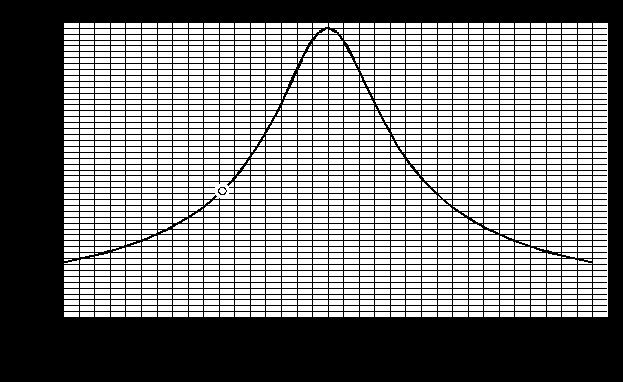 Рисунок 2 – Зависимость an(t) (точкой отмечено нормальное ускорение тела в момент времени t1 = 2,04 с) Найдем уравнение траектории движения тела.Полагая тело материальной точкой запишем кинематические уравнения движения в проекциях на оси координат. 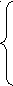 х(t) = v0·cos(α)·t; (1) у(t) = v0·sin(α)·t – g·t2/2; (2) Выразим время из (1) Сделав подстановку t в (2) получим : y(х) = x·tg(α) – g· x2/2·[v0·cos(α)] 2 Учитывая что y(х) = x·tg(α)–x2·[1 + tg2(α)] ·g/2·(v0) 2 = x·tg(79°)–x2·[1 + tg2(79°)]·9,81/2·(34) 2 = = x·5,145 – x2·(1 + 5,1452)·9,81/2·(34)2 = 5,145·х – 0,117·x2 Длина и высота полёта тела согласно (1) и (2) составят : L = v0·cos(α)·tВ = 34·cos(79°)·6.8 = 44.11 м; Н = v0·sin(α)·tA – g·tA2/2 = 34·sin (79°)·3.4 – 9,81·3.42/2 = 56.78 м; x(t1) = v0·cos(α)·t1 = 34·cos(79°)·2,04 = 13.23 м; y(t1) = v0·sin(α)·t1 – g·t12/2 = 34·sin (79°)·2.04 – 9,81·2.042/2 = 47.68 м; Потенциальная энергия в момент времени 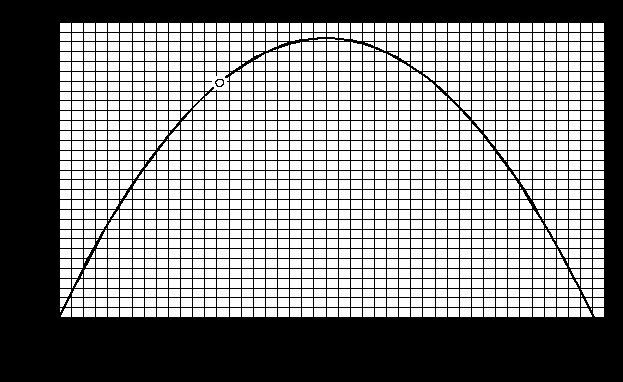 Рисунок 3 – Зависимость y(x) (точкой отмечено высота y[x(t1)] тела в момент времени t1 = 2.04 с ) ВыводВ этой работе мы исследовали движение тела, брошенного под углом к горизонту; рассчитали требуемые значения:
| |||||||||||||||||||||||