Графы, деревья, методы включения-исключения. Дискретная КМ-2. Задание Запишите свои имя и фамилию как одно слово и найдите число анаграмм такого слова. ИванКривошеев имеет 3 повторяющиеся буквы И(2 раза),В(3 раза), Е(2 раза), следовательно данное слово имеет 13!(2!3!2!) анаграмм.
 Скачать 24.09 Kb. Скачать 24.09 Kb.
|
|
Задание 4. Запишите свои имя и фамилию как одно слово и найдите число анаграмм такого слова. ИванКривошеев имеет 3 повторяющиеся буквы: И(2 раза),В(3 раза), Е(2 раза), следовательно данное слово имеет 13!/(2!3!2!) анаграмм. 13!/(2!3!2!)= 6227020800/24=259459200. 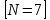 Задание 5. Решите однородное рекуррентное уравнение с начальными условиями. 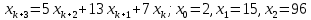 Составляем характеристическое уравнение: 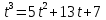 Решаем это уравнение. 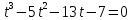 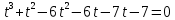 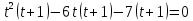 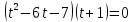 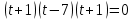 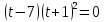 Уравнение имеет корни: 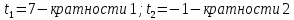 Тогда общее решение заданного однородного уравнения: 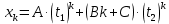 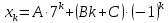 Используем начальные условия: 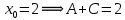 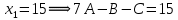 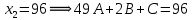 Решаем систему: 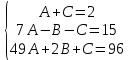 Решаем систему методом Гаусса: 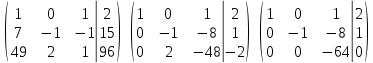 Система равносильна следующей: 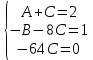 Обратным ходом находим значения 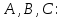 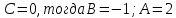 Искомое частное решение рекуррентного уравнения с заданными начальными условиями: 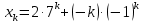 Или: 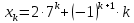 Задание 6. Решите неоднородное рекуррентное уравнение с начальным условием. 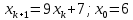 Сведём уравнение к однородному заменой переменной. Пусть 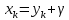 , где постоянная , где постоянная 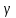 пока не известна. Подставляем в исходное уравнение: пока не известна. Подставляем в исходное уравнение: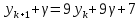 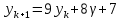 Теперь видим, что уравнение станет однородным при 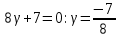 Тогда: 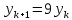 Характеристическое уравнение: 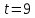 – сразу определяет корень, общее решение полученного уравнения: – сразу определяет корень, общее решение полученного уравнения: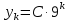 Тогда общее решение заданного уравнения: 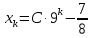 Из заданного начального условия: 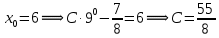 Искомое частное решение рекуррентного уравнения с заданным начальным условием: 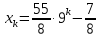 Или: 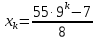 Задание 7. Найдите число перестановок элементов в 1,…,m, составляющих ровно k элементов неподвижными.
число всех сочетания из к элементов от m, где Решение: m – k = 5 – 2 = 3; 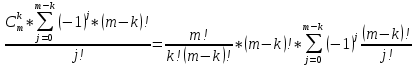 = == 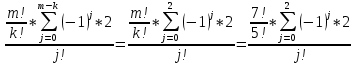 = == 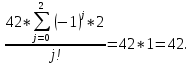 j: 0-2; 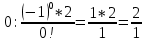 ; ;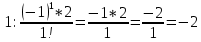 ; ;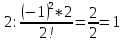 ; ;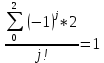 ; ;Ответ: 42. |
