соч 9 геом. Задания и схема выставления баллов
 Скачать 25.26 Kb. Скачать 25.26 Kb.
|
|
Ф.И.___________________________________________________________9 класс Суммативное оценивание по геометрии за 1 четверть ЗАДАНИЯ И СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
1 ВАРИАНТ Четырехугольник ABCD – трапеция, 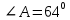 . Найдите угол между векторами . Найдите угол между векторами 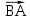 и и 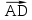 . .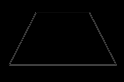 Диагонали параллелограмма PMCK пересекаются в точке О. Выразите вектор КО через векторы  и и 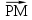 . .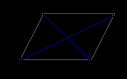 Упростите выражение 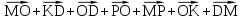 Найдите длину вектора 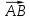 , где , где 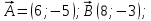 . .Даны вектор 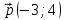 , , 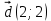 и и 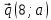 . Найдите: . Найдите: а) косинус между векторами 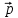 и и 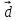 ; ;b) число а, если векторы 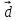 и и 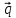 коллинеарны; коллинеарны;с) число а, если векторы 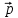 и и 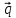 перпендикулярны. перпендикулярны.6. Решите задачу векторным методом. Выполните рисунок. Дан треугольник с вершинами М (-2;8), N (6;2), K(2;-6). Найдите длину медианы МР. Ф.И.___________________________________________________________9 класс Суммативное оценивание по геометрии за 1 четверть ЗАДАНИЯ И СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ 2 ВАРИАНТ
Четырехугольник ABCD – ромб, 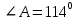 . Найдите угол между векторами . Найдите угол между векторами 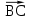 и и 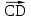 . . Диагонали параллелограмма PMCK пересекаются в точке О. Выразите вектор РО через векторы  и и 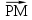 . . Упростите выражение 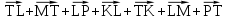 Найдите длину вектора 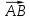 , где , где 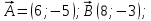 . .Даны вектор 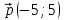 , , 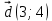 и и 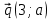 . Найдите: . Найдите: а) косинус между векторами 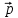 и и 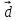 ; ;b) число а, если векторы 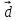 и и 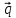 коллинеарны; коллинеарны;с) число а, если векторы 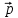 и и 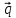 перпендикулярны. перпендикулярны.6. Решите задачу. Дан параллелограмм с вершинами М (3;-4), N (-5;3), K(1;2), L (х; у). Найдите сумму координат вершины L. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
