ВЫСТУПЛ НА ШМО 2021. Задания, развивающие математическую грамотность на уроках математики
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
|
МКОУ «СОШ №1 ЦО г. Суворова» Задания, развивающие математическую грамотность на уроках математики. (ШМО естественно-научного цикла) Подготовила: учитель математики Тонова А.Г. г. Суворов Задания, развивающие математическую грамотность на уроках математики. В исследованиях, которые ставят перед собой задачу оценки учебных достижений учащихся, традиционную для мониторинговых исследований в области оценки подготовки учащихся, разработка инструментария обычно осуществляется на основе содержания программы по математике и программных требований к подготовке учащихся (примером такого исследования является TIMSS). Учащимся предлагаются учебные задачи разного уровня сложности, позволяющие проверить умение применять изученные знания в стандартных или нестандартных учебных ситуациях. При разработке исследования PISA использован другой подход – был подготовлен отчет экспертов относительно того, какие задачи, возникающие в повседневной жизни, приходится разрешать средствами математики, и затем были определены именно те математические знания и умения, которые требуются для решения подобных задач. Очевидно, что эти знания не должны были выходить за рамки школьных программ. В то же время не ставилась цель проверить те знания, которые не находили явного применения в повседневной жизни. Поэтому не удивительно, что объем этих знаний и умений оказался существеннее уже по сравнению с тем, который формируется в школьном курсе математики. К особенностям заданий исследования PISA относятся следующие: 1) задача, поставленная вне предметной области и решаемая с помощью предметных знаний, например, по математике; 2) контекст заданий близок к проблемным ситуациям, возникающим в повседневной жизни; 3) вопросы изложены простым, ясным языком и, как правило, немногословны; 4) требуют перевода с обыденного языка на язык предметной области (математики, физики и др.); 5) формат заданий постоянно меняется, что исключает стратегию «натаскивания». Для успешного понимания и решения контекстных проблем, предложенных в тестах исследования PISA, требуется владеть рядом математических понятий, процедурами, фактами и инструментами на определенном уровне понимания и глубины усвоения. Этот отбор был сделан на основе анализа стандартов по математике 11 развитых стран мира, в числе которых были страны, показавшие в исследованиях PISA самые высокие результаты. Учитывалось, какие знания эти страны считали реально достижимыми и необходимыми для обеспечения возможности учащихся начать работать или поступить в институты для получения высшего образования, а также обеспечивают ли эти знания возможность 15-летним учащимся быть конструктивными, заинтересованными и размышляющими членами современного общества. Разработчиками концепции исследования составлен следующий перечень математических тем, владение которыми необходимо для успешного выполнения тестовых заданий в исследовании PISA-2012: Функции: понятие функции, разнообразные формы их описания и представления: словесная, символьная, табличная и графическая. Алгебраические выражения: словесная интерпретация и операции, работа со значениями переменных. Уравнения и неравенства: линейные уравнения, системы линейных уравнений и неравенства, простые квадратные уравнения, аналитические и неаналитические методы решения (например, метод «проб и ошибок»). Система координат: представление и описание данных, их расположения и зависимостей. Отношения в рамках геометрического объекта и среди геометрических объектов в двумерном и трехмерном пространстве. Пространственные фигуры и их свойства, формулы вычисления площадей поверхности и объема. Измерения: количественная характеристика свойств фигур и объектов, между фигурами и объектами. Числа и единицы измерения. Арифметические и алгебраические операции: смысл и свойства этих операций и принятых соглашений (например, законов), включая возведение чисел в натуральную степень и извлечение простых квадратных корней. Проценты, отношения и пропорции: вычисление их величины, применение пропорций и прямо пропорциональных отношений для решения проблем. Оценка: отвечающие поставленной цели приближенные значения величин и числовых выражений, включая значимые цифры и округление. Принципы подсчетов: простые сочетания и перестановки (в расчете на способ перебора вариантов). Набор данных, представление и интерпретация: природа, происхождение, наборы разнообразных данных, различные способы их представления и интерпретации. Изменчивость данных и ее описание: такие понятия, как изменчивость, распределение, центральная тенденция набора данных, способы описания и интерпретации этих данных в количественных выражениях. Выборки и составление выборок: понятие выборки и выбора из совокупностей данных, включая простые выводы на основе свойств выборок. Случайность и вероятность: Понятие случайного события, случайное изменение и его представление, частота и вероятность событий, основные аспекты понятия вероятности. В исследование PISA-2022 будут включены новые темы – это явления роста (изменения и зависимости), геометрическая аппроксимация (пространство и формы), компьютерное моделирование (количество), принятие решений в условиях неопределенности (неопределенность и данные). Тестовые задания по математике в исследовании PISA предлагаются учащимся в контекстной форме. К каждому заданию дается описание некоторой ситуации и предлагается от 1 до 3 вопросов, в которых ставятся проблемы, которые надо решить, пользуясь информацией, предложенной в описании ситуации и в самом вопросе. Поэтому успешность выполнения этих заданий существенно зависит не только от предметных знаний, но и от овладения учащимися стратегиями смыслового чтения и умения работать с текстом. К ним следует отнести, например, такие виды деятельности, как: – решать учебно-познавательные и учебно-практические задачи, требующие полного и критического понимания текста; – удерживать условия задания в процессе решения; – самоконтроль за выполнением условий (ограничений) в описании ситуации при нахождении решения и интерпретации полученного решения в рамках предложенной ситуации; – работать с информацией, представленной в различной форме (текста, таблицы, диаграммы столбчатой или круговой, схемы, рисунка, чертежа с обозначением видимых и невидимых элементов геометрической фигуры) в контексте конкретной проблемы. Кроме того, успешность в проявлении математической грамотности существенно зависит от овладения познавательными универсальными действиями логического и алгоритмического характера, общим приемом решения задач, которые в значительной степени формируются при изучении математики. Приведенный выше перечень предметных знаний, умений в основном не выходит за рамки требований к математической подготовке выпускников основной российской школы, представленных в стандарте и в Примерной основной образовательной программе образовательного учреждения. Распределение заданий в исследовании PISA выглядит следующим образом: 25% – формулировать; 25% – интерпретировать и 50% – применять. Приведу примеры заданий для формирования и оценки математической грамотности, в которых используются различные виды познавательной деятельности и формы ответов. 5 класс Задание № 1 «Команда лыжников» 1.1 Прочитайте текст и выполните задания 1-2. Тренер школьной команды лыжников для организации летних тренировок провёл опрос спортсменов, чтобы узнать, есть ли у них скейтборды и лыжероллеры. На вопрос ответили 12 человек. Результаты представлены в таблице 1. Таблица 1 Наличие скейтборда и лыжероллеров у спортсменов
Обозначения: + есть, – нет 1. На основе данных таблицы 1 заполните таблицу 2, которая показывает, сколько спортсменов имеют скейтборды и сколько спортсменов имеют лыжероллеры. Таблица 2 Количество снаряжения у спортсменов
2. Характеристики задания. • Содержательная область оценки: неопределённость и данные. • Компетентностная область оценки: применять • Контекст: личный • Уровень сложности: низкий. • Формат ответа: задание с несколькими краткими ответами (отдельные поля для ответов). • Объект оценки: заполнение готовой таблицы 3. Система оценивания.
1.2 На основе данных таблицы 1 составлены следующие утверждения. Отметьте знаком P верные. ¨ У каждого спортсмена есть и лыжероллеры, и скейтборд. ¨ Если у спортсмена есть скейтборд, то у него нет лыжероллеров. ¨ У всех спортсменов есть какое-нибудь снаряжение для тренировок. ¨ У всех членов команды скейтбордов больше, чем лыжероллеров. ¨ Чтобы проводить тренировки, нужно еще 5 комплектов. Характеристики задания • Содержательная область оценки: неопределённость и данные • Компетентностная область оценки: рассуждать • Контекст: общественный • Уровень сложности: средний • Формат ответа: Задание с выбором нескольких верных ответов • Объект оценки: проверка истинности утверждений относительно данных таблицы, понимать логические связки «если, то», «есть», «все», «каждый», «и» 3.Система оценивания
класс Задание № 2 «Опрос пятиклассников» 1. 1.1. Прочитайте текст и выполните задания 1-2. В школе пятиклассников попросили ответить на вопрос: «Какой из учебных предметов тебе нравится больше других?» и указать только один из предложенных вариантов. На вопрос ответили 35 учеников. Ниже на диаграмме 1 представлены результаты опроса. Диаграмма 1 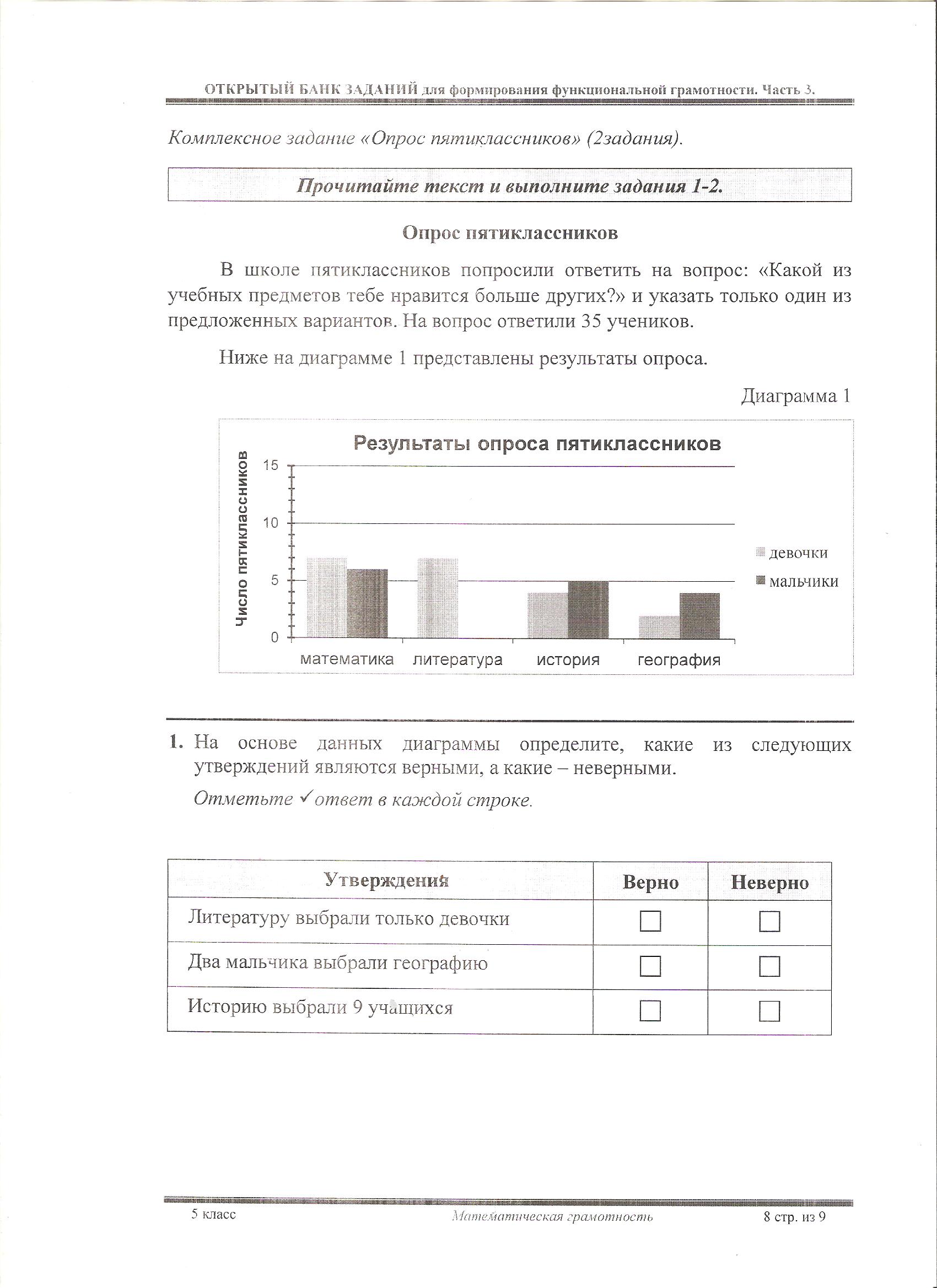 1. На основе данных диаграммы определите, какие из следующих утверждений являются верными, а какие – неверными. Отметьте ✓ответ в каждой строке.  2. Характеристики задания. • Содержательная область оценки: неопределенность и данные • Компетентностная область оценки: рассуждать • Контекст: личный • Уровень сложности: средний • Формат ответа: задание с комплексным множественным выбором • Объект оценки: чтение и интерпретация данных диаграммы, проверка истинности утверждений на основе данных диаграммы. Система оценивания.
1.2 На основании данных диаграммы 1 узнайте, сколько мальчиков и сколько девочек участвовали в опросе. Изобразите эти данные на Диаграмме 2. Диаграмма 2 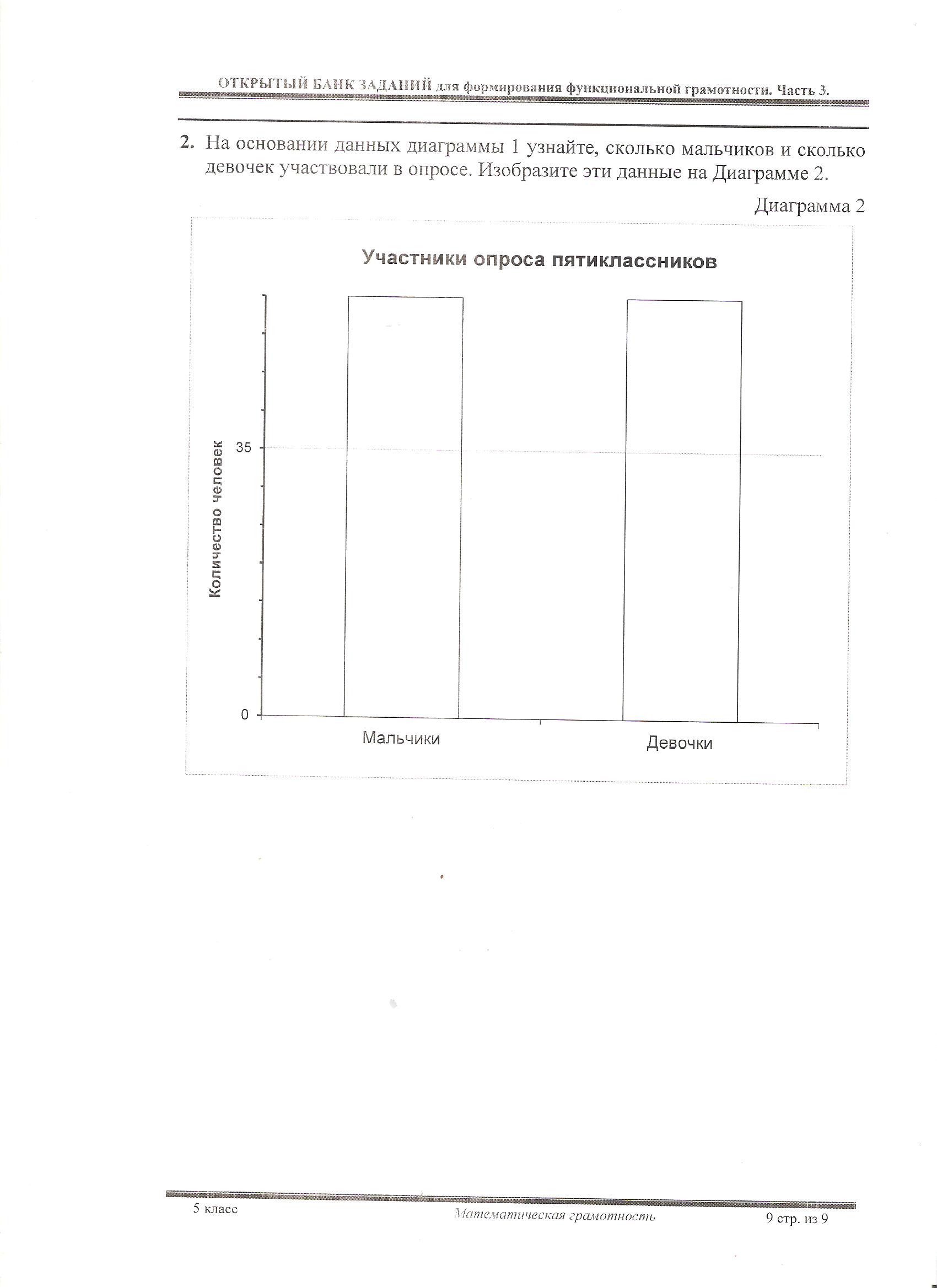 2. Характеристики задания • Содержательная область оценки: неопределенность и данные • Компетентностная область оценки: применять • Контекст: образовательный • Уровень сложности: высокий • Формат ответа: задание с развернутым ответом (в виде рисунка или рисунка и текста) • Объект оценки: чтение шкалы, построение столбцов диаграммы на основе полученных данных Система оценивания
класс Задание № 3 «Дорога до дачи» Прочитайте текст и выполните задания 1-2.  Всем хорошо известно, как важны хорошие дороги, по которым можно в кратчайшие сроки перевозить необходимые грузы и перемещаться пассажирам. На автомобильной трассе М4 «Дон» в пределах Московского региона ввели в эксплуатацию три скоростных участка, на которых можно развивать скорость до 130 км/час. Скоростные участки трассы расположены от Москвы: первый – от отметки 51 км до отметки 71 км; второй – от отметки 76 км до отметки 103 км, третий – от отметки 113 км до отметки 120 км. В субботу семья Ивановых выехала на автомобиле на дачу, которая расположена в 120 км от Москвы. В 8 ч утра они начали движение по трассе «Дон» и воспользовались скоростными её участками. График их движения по трассе изображён на рисунке. 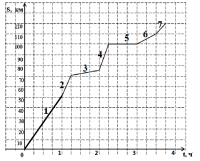 1.1. Опишите, что могло произойти на 100-м километре трассы. Ответ поясните. Ответ: ____________________________________________________________________ Характеристики задания • Содержательная область: изменение и зависимости • Компетентностная область: интерпретировать • Контекст: личная жизнь • Уровень сложности: низкий • Формат ответа: с развернутым ответом (в виде текста) • Объект оценки: чтение, понимание графика движения автомобиля и интерпретация результата анализа графика 3. Система оценивания
На участке трассы от отметки 71 км до отметки 76 км идут дорожные работы по соединению двух первых скоростных участков в единый скоростной участок. За какое наименьшее время можно будет преодолевать этот объединённый скоростной участок после завершения дорожных работ? Ответ дайте в минутах. Ответ: ____________________________________________________________________ Решение: __________________________________________________________________ __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ 2. Характеристики задания . • Содержательная область: изменение и зависимости • Компетентностная область: формулировать • Контекст: личная жизнь • Уровень сложности: средний • Формат ответа: с развернутым ответом (в виде текста решения) • Объект оценки: вычисление минимального времени движения автомобиля с выбранной скоростью в реальной жизни Система оценивания.
класс Задание № 4 «Стеллаж из ящиков» Прочитайте текст и выполните задания 1-2. Из нескольких одинаковых ящиков в форме куба сделали стеллаж, изображённый на фото. Сторона куба равна 30 см.  1. Решено доработать стеллаж и сделать две дверцы, которые закрыли бы ниши, образованные стенками соседних ящиков. На фото они обозначены цифрами 1 и 2.  1.1 Для каждой дверцы: а) укажите в таблице соответствующую её форме геометрическую фигуру: равносторонний треугольник, равнобедренный треугольник, квадрат, ромб, трапеция; б) вычислите длины сторон и величины углов выбранных фигур, занесите их в таблицу.
Характеристики задания. • Содержательная область: пространство и форма • Компетентностная область: интерпретировать • Контекст: образование/ профессиональная деятельность • Уровень сложности: средний • Формат ответа: с краткими ответами • Объект оценки: распознавание геометрических фигур, определение величины их линейных и угловых элементов Система оценивания.
1.2 Можно ли разместить такой стеллаж в стенной нише, если высота ниши составляет 1 м? Ответ: ____________________________________________ Решение: _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Характеристики задания. • Содержательная область: пространство и форма • Компетентностная область: рассуждать • Контекст: образование/Профессиональная деятельность • Уровень сложности: высокий • Формат ответа: с развернутым ответом (в виде текста или в виде рисунка и текста) • Объект оценки: использование основных свойств прямоугольных треугольников, соотношений между сторонами и углами в прямоугольном треугольнике, теоремы Пифагора Система оценивания:
|

