аб. Задания школьного этапа Всероссийской олимпиады по математике. Задания школьного этапа Всероссийской олимпиады по математике 20182019 учебный год 7 класс. Задание 1
 Скачать 130.45 Kb. Скачать 130.45 Kb.
|
|
Задания школьного этапа Всероссийской олимпиады по математике 2018-2019 учебный год 7 класс. Задание № 1 Семь девяток выписали подряд: 9 9 9 9 9 9 9. Поставьте между некоторыми из них знаки "+" или "-", чтобы получившееся выражение равнялось 1989. Решение: 999+999 - 9 = 1989. Задание № 2 Решите уравнение│7 – х│ = 9,3 Решение: 7 – х = 9,3 или 7 – х = - 9,3, поэтому х = 7 – 9,3 или х = 7 + 9,3 и так х = - 2,3 или х = 16,3 Задание № 3 Человек шел со скоростью 3 км/ч вдоль трамвайной линии и считал трамваи. И те, которые двигались ему навстречу, и те, которые обгоняли его. Человек насчитал 40 трамваев, обогнавших его, и 60 встречных. Предположим, что трамваи движутся равномерно, с одинаковыми промежутками между собой (в задаче это вполне возможно). Какова средняя скорость движения трамваев? Решение: 15 км/ч. Относительные скорости трамваев, идущих вдогонку и навстречу человеку, пропорциональны числу трамваев, поравнявшихся с ним. Следовательно, можно составить уравнение: (х-3):(х+3)=40:60; 60(х-3)=40(х+3). Решая уравнение получаем х=15. Задание №4 Проведите шесть прямых и отметьте на них 11 точек так, чтобы на каждой прямой было отмечено ровно четыре точки. Р 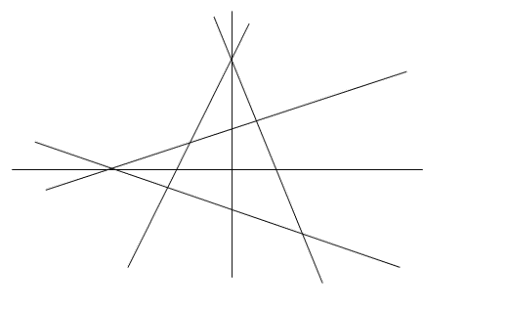 ешение: Задание № 5 Решите ребус, если известно, что наибольшая цифра в числе СИЛЕН равна 5: +РЕШИ ЕСЛИ СИЛЕН Решение. Так как наибольшая цифра в числе «СИЛЕН» равна 5, а С =1, то остальные 4 цифры в данном числе будут 2,3,4,5. Так как Н Е (в самом деле, так Е +1 = Л, то Л Е, ведь Л и Е меньше 5 по условию), то Л = 5, Е = 3. А тогда уже легко находятся остальные цифры: Ш = 8, Р = 9. В итоге получается: 9382 + 3152 = 12534 Всероссийская олимпиада школьников по математике. 2017–2018 уч. год. Школьный этап. 7 класс 1. (7 баллов) Числитель и знаменатель дроби — положительные числа. Числитель увеличили на 1, а знаменатель — на 100. Может ли полученная дробь оказаться больше исходной? Ответ: да. Решение. Например, 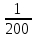 < <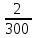 Есть и много других примеров. 2. (7 баллов) Ребятам дали задания перевести скорость черепахи из сантиметров в секунду в метры в минуту. Маша получила ответ 25 м/мин, но при этом считала, что в метре 60 см, а в минуте 100 секунд. Помогите Маше найти правильный ответ. Ответ: 9 м/мин. Решение. Черепаха за одну М´ашину «минуту» преодолевает расстояние в 25 Машиных «метров», то есть за 100 секунд проползает 25 · 60 санти- метров. Тогда скорость черепахи равна 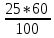 = 15 см/сек. Значит, за 60 = 15 см/сек. Значит, за 60секунд черепаха проползет 15 · 60 сантиметров, то есть 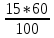 = 9 метров. = 9 метров.3. (7 баллов) В некоторый момент времени Аня измерила угол между часовой и минутной стрелками своих часов. Ровно через один час она снова измерила угол между стрелками. Угол оказался таким же. Каким мог быть этот угол? (Разберите все случаи.) Ответ: 15◦ либо 165◦ 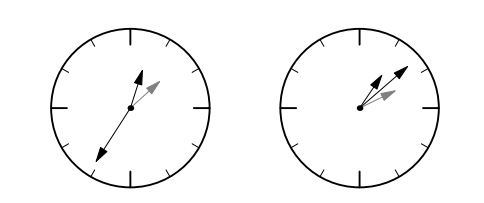 Решение. Через 1 час минутная стрелка остается на своем месте. При этом часовая стрелка повернулась на 30◦ Раз угол не изменился, то минутная стрелка делит пополам один из углов между положениями часовой стрелки (либо тот, который 30◦, либо дополнительный угол в 330◦). Значит, либо часовая стрелка была на 15◦раньше, либо на 165◦позже. 4. (7 баллов) Два пешехода вышли на рассвете. Каждый шёл с постоянной скоростью. Один шёл из A в B, другой — из B в A. Они встретились в полдень (т. е. ровно в 12 часов) и, не прекращая движения, пришли: один — в B в 4 часа вечера, а другой – в A в 9 часов вечера. В котором часу в тот день был рассвет? Ответ: в 6 утра.  5. (7 баллов) Определите, в каком количестве точек пересекаются 10 прямых, если среди них есть только две параллельные и ровно три из этих прямых пересекаются в одной точке. Ответ: 42. Решение. Пронумеруем прямые так, чтобы именно прямые 1, 2 и 3 пересекались в одной точке (эту точку обозначим за X). Выпишем всевозможные пары прямых (1 и 2, 1 и 3, 1 и 4, . . . , 8 и 9, 8 и 10, 9 и 10) и их точки пересечения. Всего пар прямых 45 (пар вида 1 и ` ровно 9, пар вида 2 и ровно 8 и так далее; 9+ 8+ 7+ 6+ 5+ 4+ 3+ 2+ 1 = 45). По условию ровно две прямые параллельны. Значит, всего будет выписано 44 точки пересечения. При этом все точки пересечения прямых кроме X будут выписаны ровно по одному разу, а точка X появится трижды: для пар прямых 1 и 2, 1 и 3, 2 и 3. Сотрем из списка точек пересечения две лишние буквы X. Останутся ровно 42 точки, и на этот раз все точки пересечения будут посчитаны ровно по одному разу. Почему две прямые перпендикулярные к третьей не пересекаются? Потому что они будут являться параллельными, а параллельные прямые не пересекаются. Через две точки можно провести прямую, и притом только одну, то есть и из точки, не лежащей на прямой можно провести только одну перпендикулярную прямую к данной прямой. |
