МатАнализ. Поверхность второго порядка. Поверхность второго порядка. Заданные постоянные числа, а
 Скачать 1.63 Mb.
|
|
Уравнение 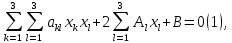 где аkl = аlk, Аl, В – заданные постоянные числа, а х = (х1, х2, х3) – переменная точка в R3, определяет некоторое множество точек в R3, называемое поверхностью второго порядка. Если уравнение (1) не удовлетворяется ни одной действительной точкой х = (х1, х2, х3), то говорят, что оно определяет мнимую поверхность. Частные случаи уравнения (1): Поверхности вращения - Эллипсоид 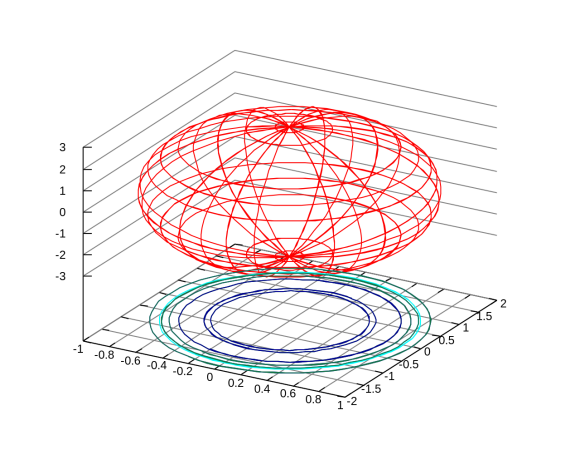 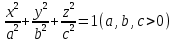 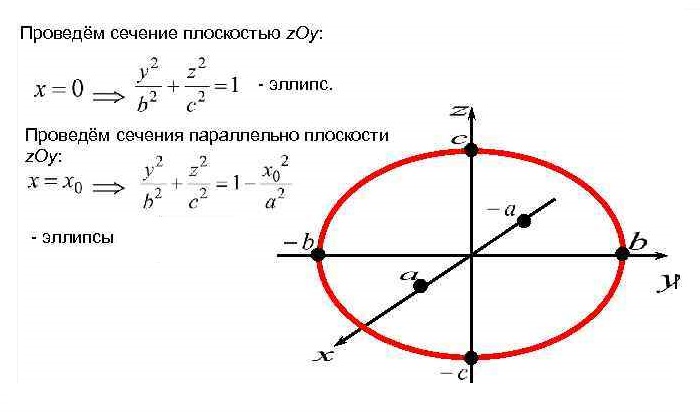 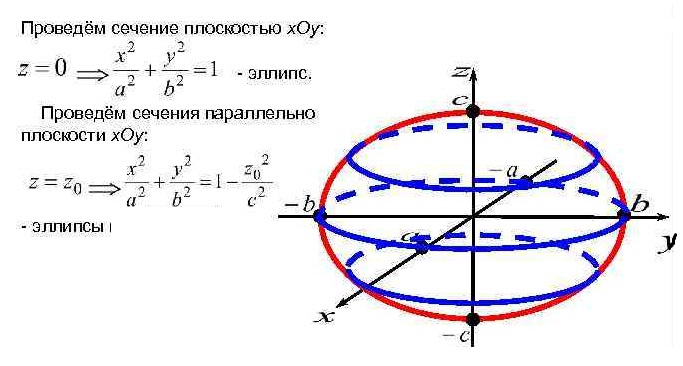 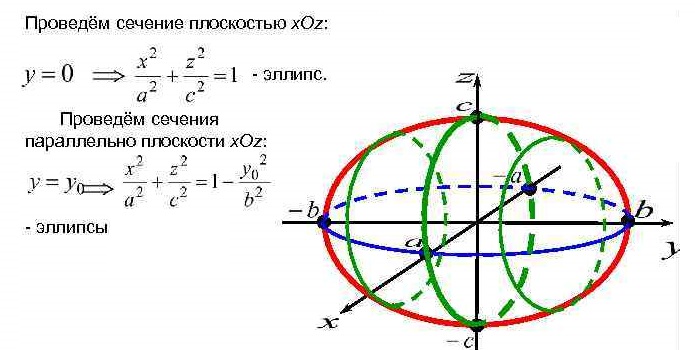 - Однополостный гиперболоид 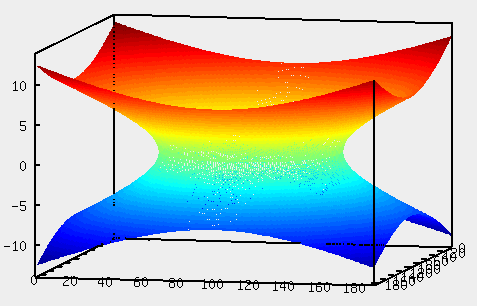 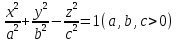 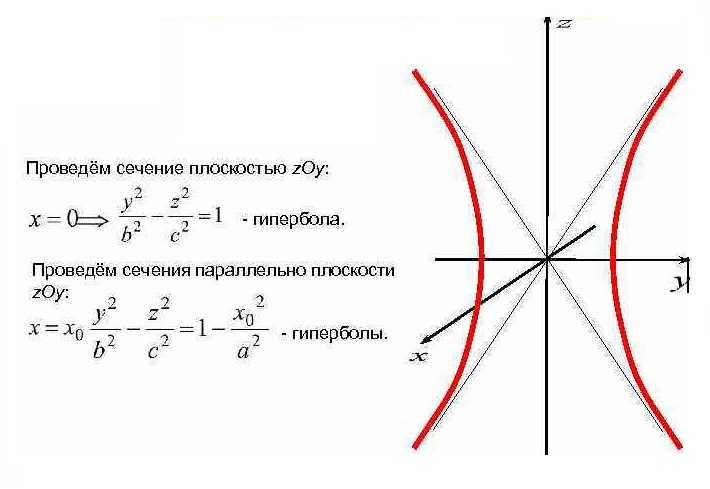 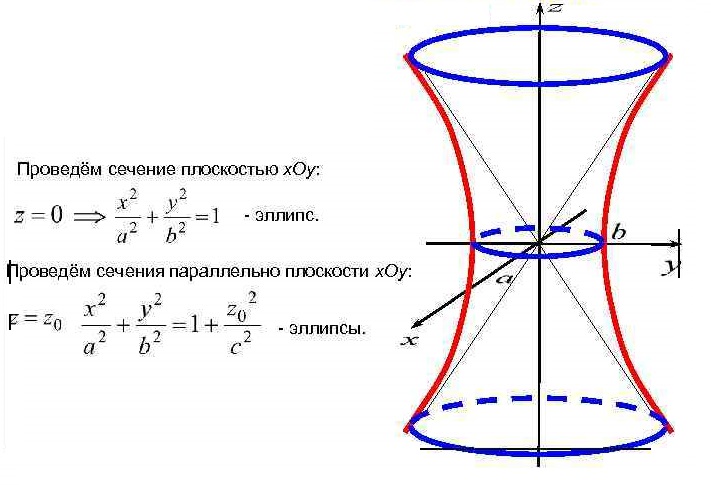 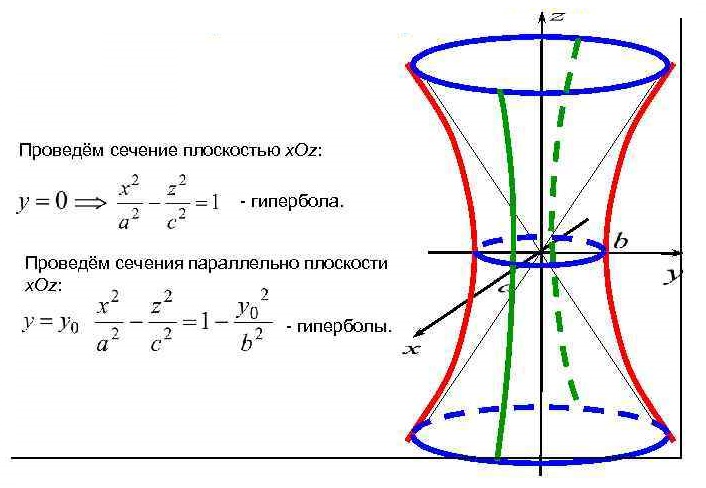 - Двуполостный гиперболоид 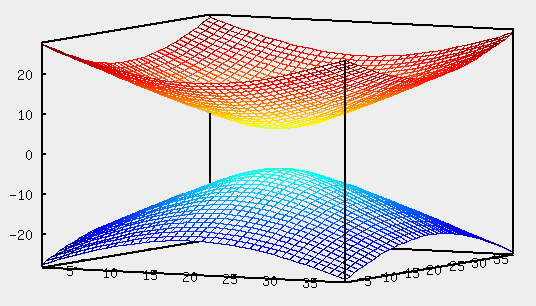  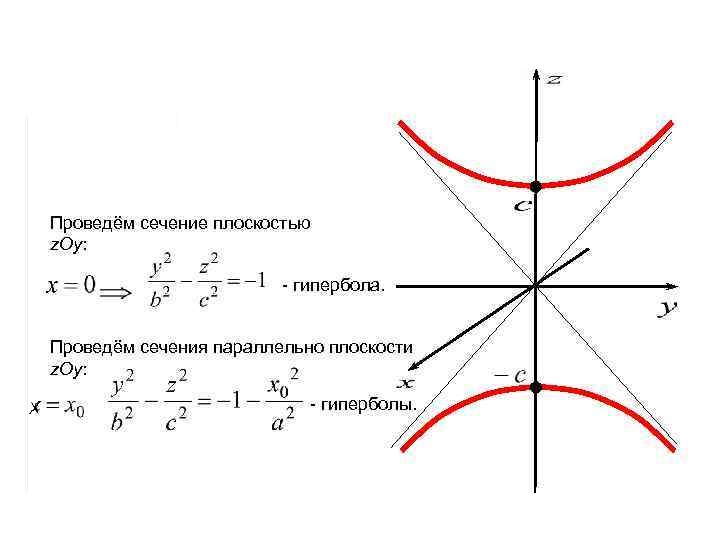 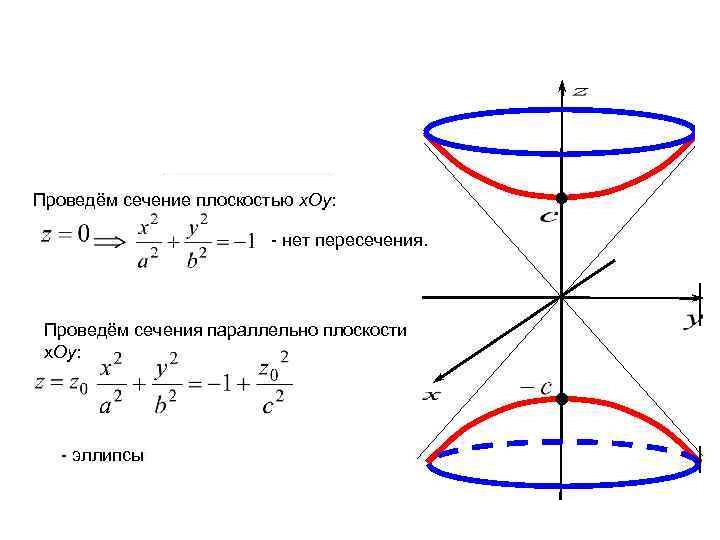 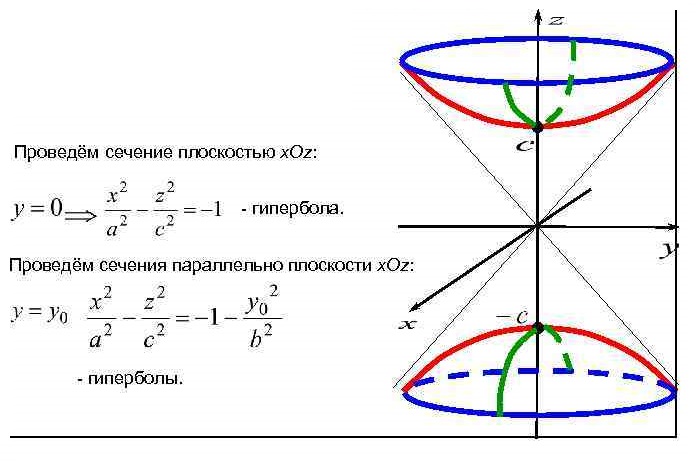 - Эллиптический параболоид 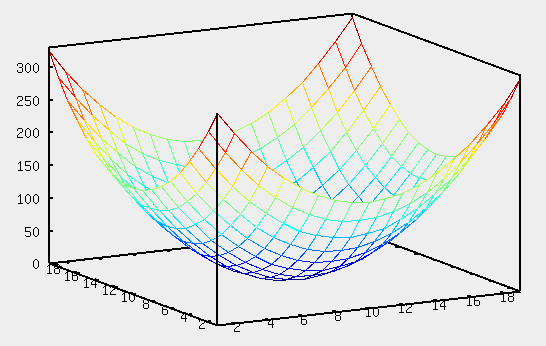 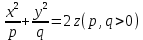 Если a=b{\displaystyle a=b}, то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы, параметр которой p=a2=b2{\displaystyle p=a^{2}=b^{2}}, вокруг вертикальной оси, проходящей через вершину и фокус данной параболы. Пересечение эллиптического параболоида с плоскостью z=z0>0{\displaystyle z=z_{0}>0} является эллипсом. Пересечение эллиптического параболоида с плоскостью {\displaystyle x=x_{0}} x=x0 или y=y0 {\displaystyle y=y_{0}} является параболой. 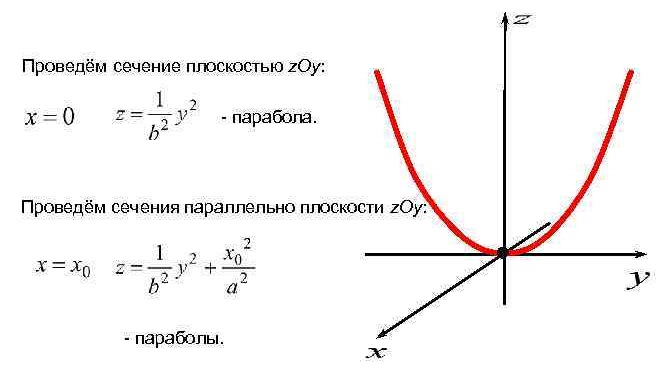 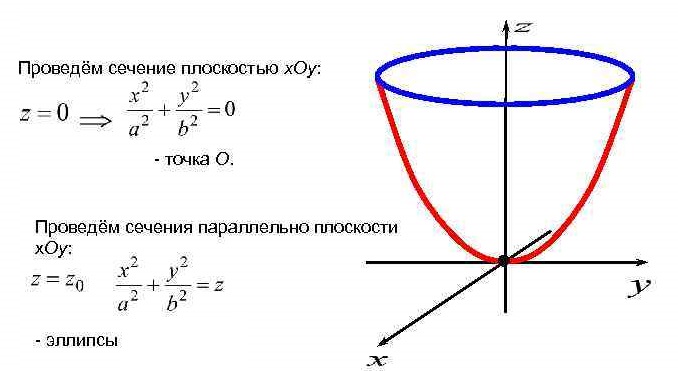 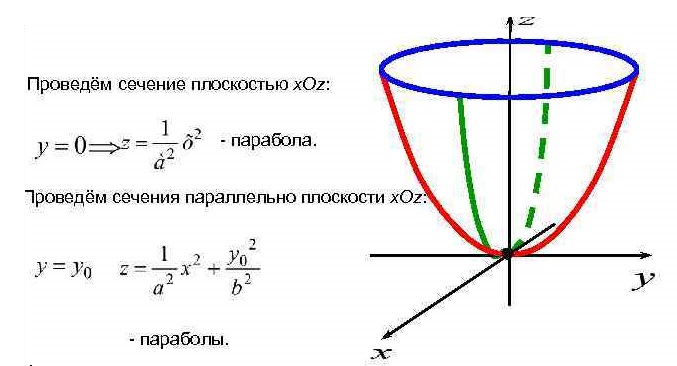 - Гиперболический параболоид 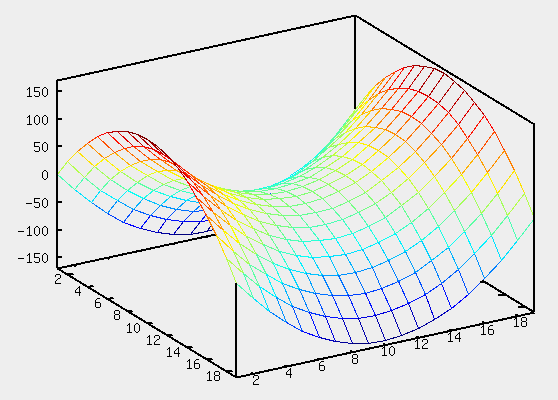 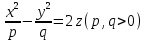 Пересечение гиперболического параболоида с плоскостью {\displaystyle z=z_{0}}z=z0 является гиперболой. Пересечение гиперболического параболоида с плоскостью {\displaystyle x=x_{0}} x=x0 или y=y0 {\displaystyle y=y_{0}} является параболой. Ввиду геометрической схожести гиперболический параболоид часто называют «седлом». 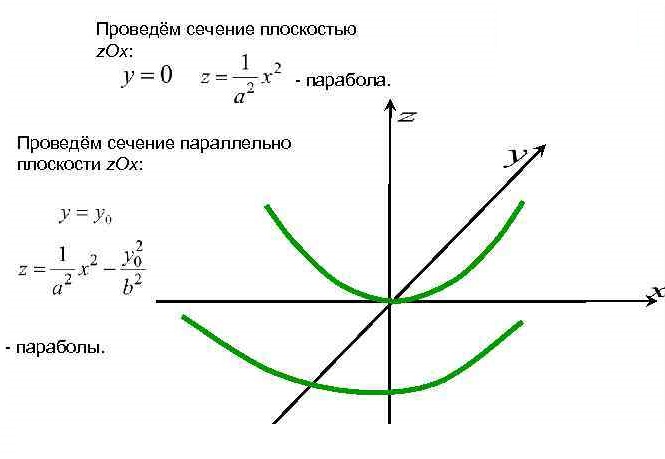 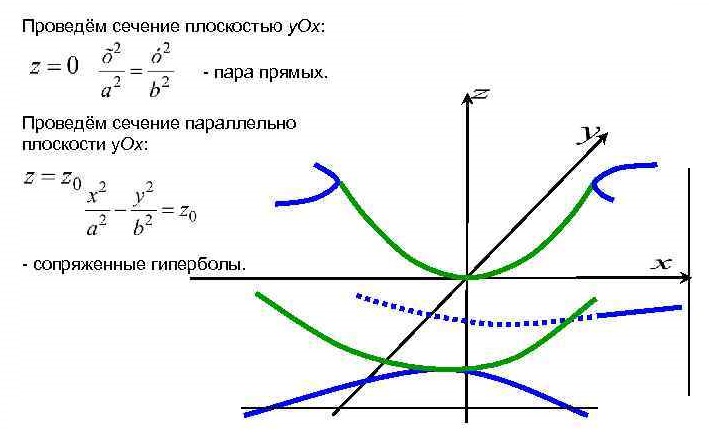 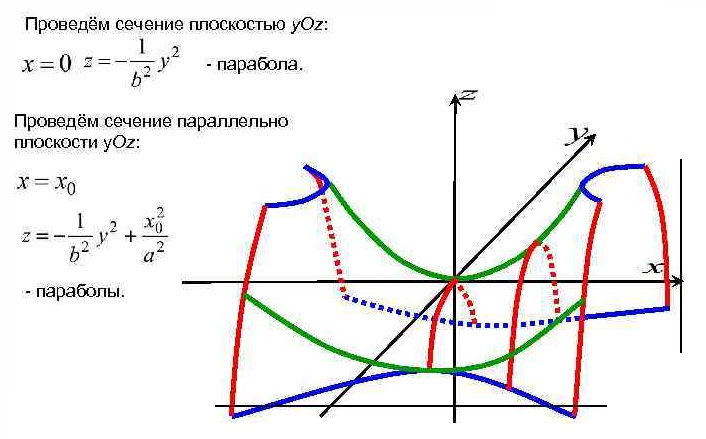 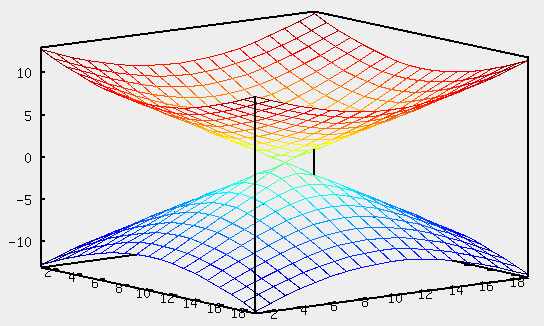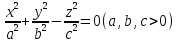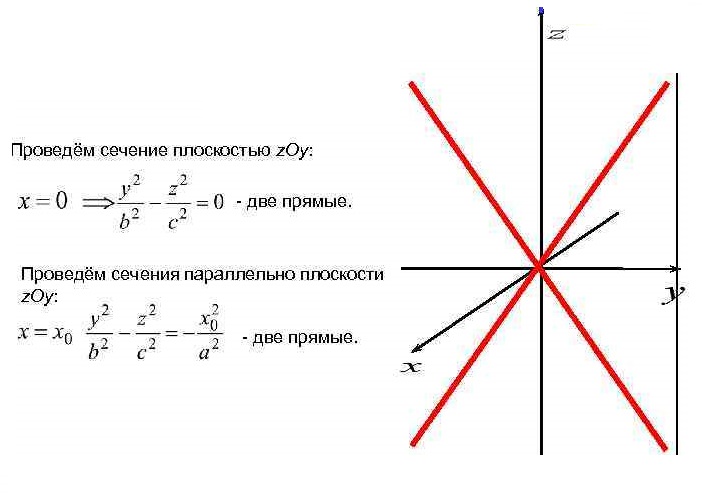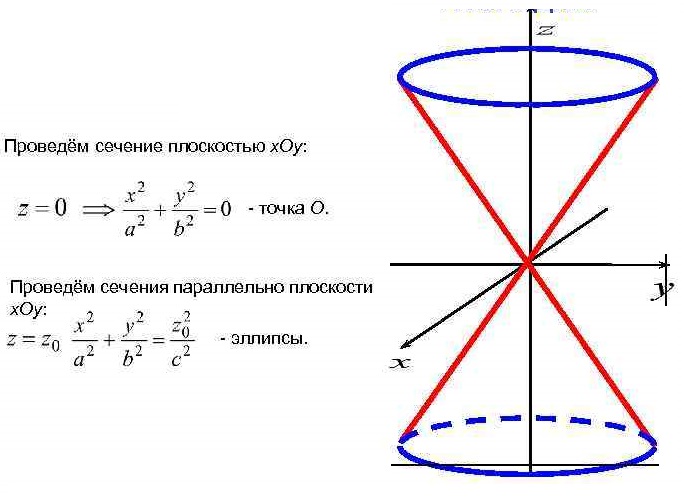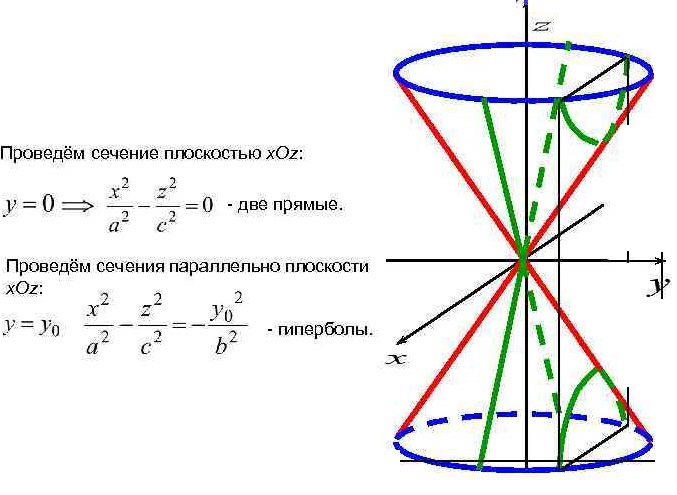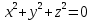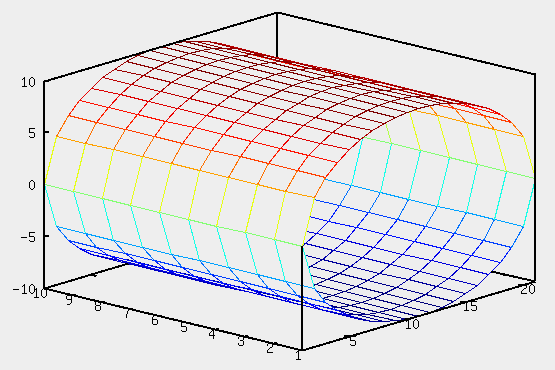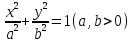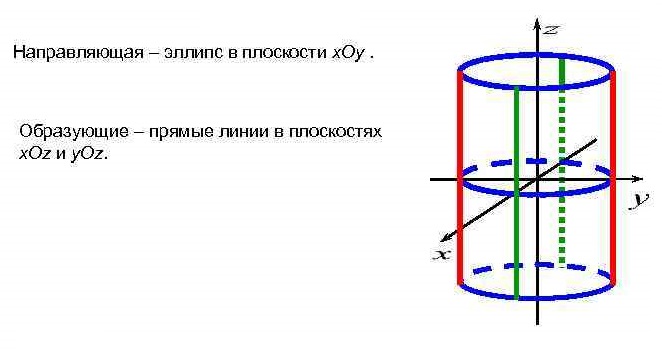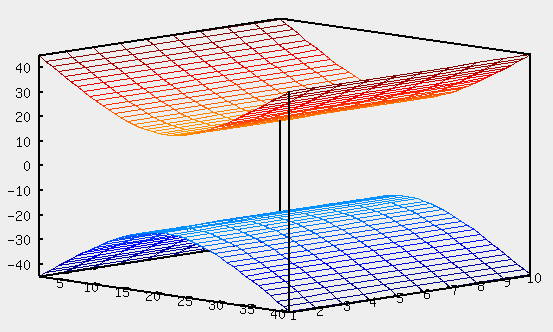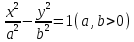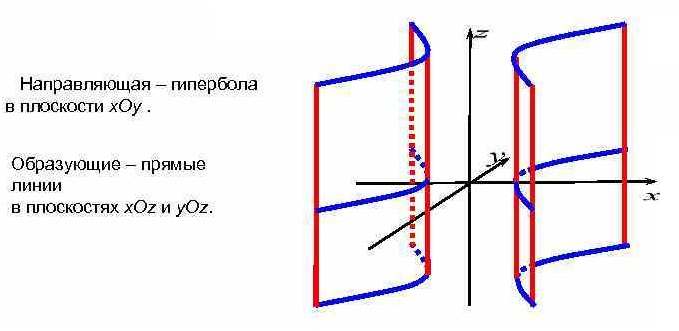Конические поверхности - Конус второго порядка      Точка  Цилиндрические поверхности Цилиндр эллиптический    Ц  илиндр гиперболический   Цилиндр параболический 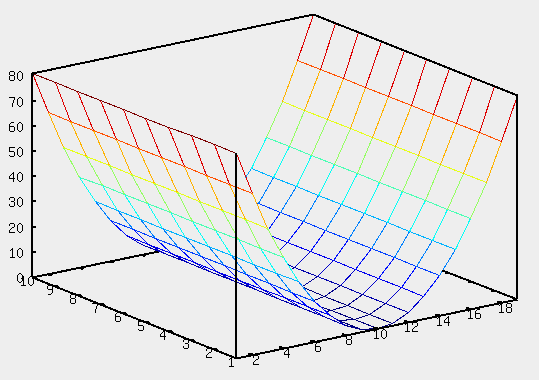 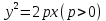 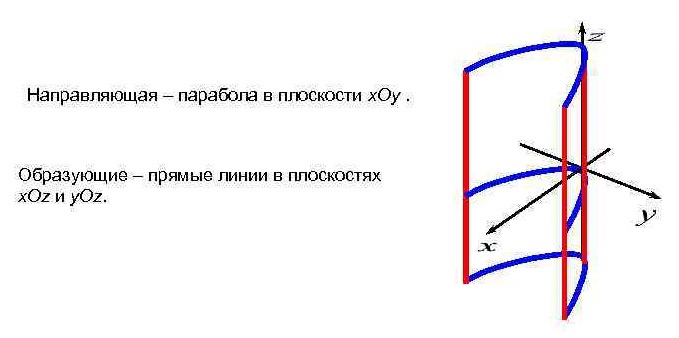 Пара пересекающихся плоскостей 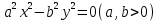 Пара параллельных или совпадающих плоскостей 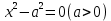 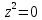 - Прямая 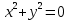 |