32_Поляризация света. Закон Брюстера tg b n 21

• Название: Закон Брюстера tg b n 21
• Дата: 02.11.2018
• Размер: 153.5 Kb.
• Имя файла: 32_Поляризация света.doc
• Тип: Закон; #55230

§ 32. ПОЛЯРИЗАЦИЯ СВЕТА

Основные формулы

• Закон Брюстера

tg ε_B =n₂₁,

где ε_B — угол падения, при котором отраженная световая волна полностью поляризована; n₂₁ — относительный показатель прелом­ления.

• Закон Малюса

I=I₀cos²α,

где I — интенсивность плоскополяризованного света, прошедшего через анализатор; I₀ — интенсивность плоскополяризованного све­та, падающего на анализатор; α — угол между направлением колеба­ний светового вектора волны, падающей на анализатор, и плоско­стью пропускания анализатора.

• Степень поляризации света

,

где I_max и I_min — максимальная и минимальная интенсивности частично поляризованного света, пропускаемого анализатором.

• Угол поворота φ плоскости поляризации оптически актив­ными веществами определяется соотношениями:

а) в твердых телах φ=αd, где α — постоянная вращения; d — длина пути, пройденного светом в оптически активном веществе;

б) в чистых жидкостях φ=[α]ρd, где [α] — удельное вращение; ρ — плотность жидкости;

в) в растворах φ=[α]Cd, где С — массовая концентрация опти­чески активного вещества в растворе.

Примеры решения задач

Пример 1. Пучок естественного света падает на полированную поверхность стеклянной пластины, погруженной в жидкость. Отраженный от пластины пучок света составляет угол φ=97° с падаю­щим пучком (рис. 32.1). Определить показатель преломления n жидкости, если отраженный свет полностью по­ляризован.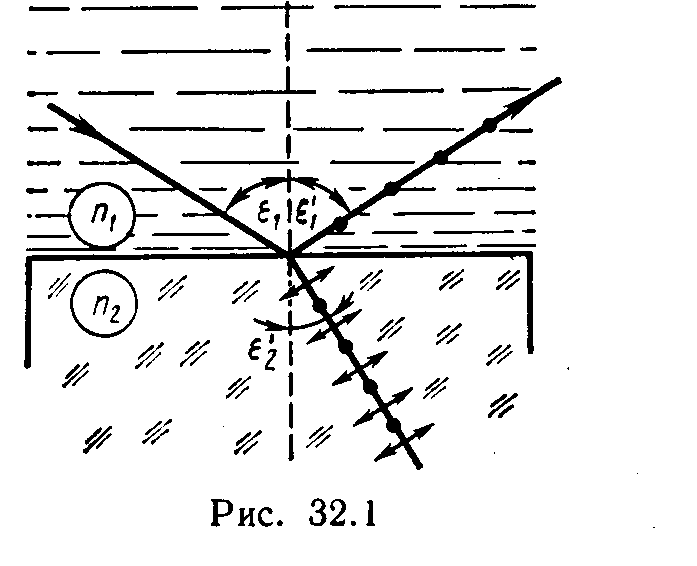



Решение. Согласно закону Брюстера, свет, отраженный от ди­электрика, полностью поляризован в том случае, если тангенс угла паде­ния

tg ε_1B=n₂₁,

где n₂₁ — относительный показатель преломления второй среды (стекла) относительно первой (жидкости).

Относительный показатель преломления равен отношению аб­солютных показателей преломления этих сред. Следовательно,

tg ε_1B=n₂/n₁.

Согласно условию задачи, отраженный луч повернут на угол φ от­носительно падающего луча. Так как угол падения равен углу отра­жения, то ε_1B=φ/2 и, следовательно, tg(φ/2)=n₂/n₁, откуда

.

Сделав подстановку числовых значений, получим n₁=l,33.

Пример 2. Два николя N₁ и N₂ расположены так, что угол a между их плоскостями пропускания равен 60°. Определить: 1) во сколько раз уменьшится интенсивность света при прохождении че­рез один николь (N₁); 2) во сколько раз уменьшится интенсивность света при прохождении через оба николя? При прохождении каждо­го из николей потери на отражение и поглощение света составляют 5 %.

Решение 1. Пучок естественного света, падая на грань ни­коля N₁ (рис. 32.2), расщепляется вследствие двойного лучепрелом­ления на два пучка: обыкновенный и необыкновенный. Оба пучка одинаковы по интенсивности и полностью поляризованы. Плоскость колебаний для необыкновенного пучка лежит в плоскости чертежа (плоскость главного сечения). Плоскость колебаний для обыкновенного пучка перпендикулярна плоскости чертежа. Обыкновенный пучок (o) вследствие полного отражения от границы АВ отбрасы­вается на зачерненную поверхность призмы и поглощается ею. Необыкновенный пучок (е) проходит через николь. При этом интен­сивность света уменьшается вследствие поглощения в веществе николя.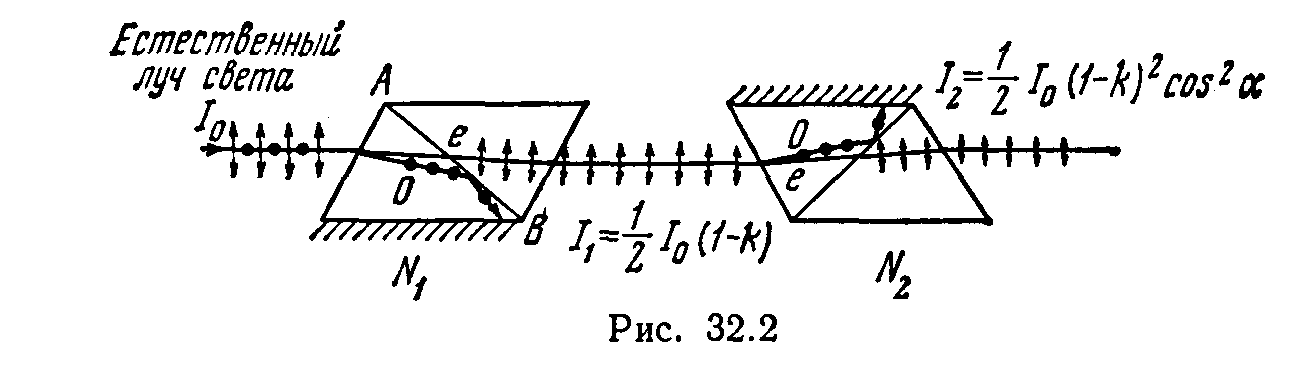



Таким образом, интенсивность света, прошедшего через николь N₁,

I₁=1/2I₀(1-k),

где k=0,05— относительная потеря интенсивности света в николе; I₀ — интенсивность естественного света, падающего на николь N₁.

Относительное уменьшение интенсивности света получим, разде­лив интенсивность I₀ естественного света на интенсивность I₁ по­ляризованного света:

.

Подставив числовые значения, найдем

I₀/I₁=2,10.

Таким образом, интенсивность света при прохождении через николь N₁ уменьшается в 2,10 раза.

2. Пучок плоскополяризованного света интенсивности I₁ падает на николь N₂ и также расщепляется на обыкновенный и необыкновен­ный. Обыкновенный пучок полностью поглощается в николе, а ин­тенсивность необыкновенного пучка света, вышедшего из николя, определяется законом Малюса (без учета поглощения в этом николе):

I₂=I₁cos²α

где α — угол между плоскостью колебаний в поляризованном пучке и плоскостью пропускания николя N₂.

Учитывая потери интенсивности во втором николе, получим

I₂=I₁ (l—k) cos² α.

Искомое уменьшение интенсивности при прохождении света че­рез оба николя найдем, разделив интенсивность I₀ естественного света на интенсивность I₂ света, прошедшего систему из двух николей:

.
З
аменив I₀/I₁ его выражением по формуле (1), получим

Подставив данные, произведем вычисления:


Таким образом, после прохождения света через два николя интен­сивность его уменьшится в 8,86 раза.

Пример 3. Пучок частично-поляризованного света рассматри­вается через николь. Первоначально николь установлен так, что его плоскость пропускания параллельна плоскости колебаний линейно-поляризованного света. При повороте николя на угол (φ=60° интен­сивность пропускаемого им света уменьшилась в k=2 раза. Опреде­лить отношение I_e/I_п интенсивностей естественного и линейно-поля­ризованного света, составляющих данный частично-поляризован­ный свет, а также степень поляризации Р пучка света.

Р
ешение. Отношение интенсивности I_e естественного света к интенсивности I_e поляризованного света найдем из следующих сооб­ражений. При первоначальном положении николя он полностью пропустит линейно-поляризованный свет и половину интенсивности естественного света. Общая интенсивность пропущенного при этом света

П
ри втором положении николя интенсивность пропущенного по­ляризованного света определится по закону Малюса, а интенсив­ность пропущенного естественного света, как и в первом случае, будет равна половине интенсивности естественного света, падающего на николь. Общая интенсивность во втором случае

В соответствии с условием задачи I₁=k*I₂, или


Подставив сюда значение угла φ , k и произведя вычисления, по­лучим

I_e/I_п = 1, или I_e = I_п ,

т. е. интенсивности естественного и поляризованного света в задан­ном пучке равны между собой.

Степень поляризации частично-поляризованного света определя­ется соотношением

P = (I_max – I_min)/(I_max + I_min), (1)

где I_max и I_min — соответственно максимальная и минимальная ин­тенсивности света, пропущенного через николь.

Максимальная интенсивность I_max = I₁ = I_п + ½ I_e, или, учи­тывая, что I_e = I_п

I_max = 3/2 I_п
Минимальная интенсивность соответствует положению николя, при котором плоскость пропускания его перпендикулярна плоско­сти колебаний линейно-поляризованного света. При таком положе­нии николя поляризованный свет будет полностью погашен и через николь пройдет только половина интенсивности естественного света. Общая интенсивность выразится равенством

I_min = ½ I_e= ½ I_п

П
одставив найденные выражения I_max и I_min в формулу (1), получим

Следовательно, степень поляризации пучка света

P = ½ .

Пример 4. Пластинка кварца толщиной d₁=1 мм, вырезанная перпендикулярно оптической оси кристалла, поворачивает пло­скость поляризации монохроматического света определенной длины волны на угол φ₁=20°. Определить: 1) какова должна быть толщина d₂ кварцевой пластинки, помещенной между двумя «параллельными» николями, чтобы свет был полностью погашен; 2) какой длины l труб­ку с раствором сахара массовой концентрацией С=0,4 кг/л надо поместить между николями для получения того же эффекта? Удель­ное вращение [α] раствора сахара равно 0,665 град/(м*кг*м^-3).

Решение. 1. Угол поворота плоскости поляризации кварце­вой пластинкой определяется соотношением φ = α *d.

Пользуясь этой формулой, выразим искомую толщину d₂ пла­стинки:

d₂ = φ₂ / α (1)

где φ₂ — угол поворота плоскости поляризации, при котором свет будет полностью погашен (φ₂ =90°).

Постоянную вращения α для кварца найдем также из формулы φ=α*d, подставив в нее заданные в условии задачи значения d₁ и φ₁:

α = φ₁ / d₁

Подставив это выражение α в формулу (1), получим

d₂ = (φ₂/ φ₁) d₁

Произведя вычисления по этой формуле, найдем толщину пла­стинки:

d₂ = 4,5 мм.

2. Длину трубки с сахарным раствором найдем из соотношения φ₂=[α]Cd, выражающего угол поворота плоскости поляризации раствором сахара, где d — толщина раствора сахара (принимается равной длине l трубки). Отсюда получим

l = φ₂/([α]C).

Подставив сюда значения φ₂, [α], C=0,4 кг/л ==400 кг/м³ и произведя вычисления, найдем

l=3,8 дм.

Задачи

Закон Брюстера. Закон Малюса

32.1. Пучок света, идущий в воздухе, падает на поверхность жидкости под углом ε₁=54°. Определить угол преломления ε`₂ пуч­ка, если отраженный пучок полностью поляризован.

32.2. На какой угловой высоте φ над горизонтом должно нахо­диться Солнце, чтобы солнечный свет, отраженный от поверхности воды, был полностью поляризован?

32.3. Пучок естественного света, идущий в воде, отражается от грани алмаза, погруженного в воду. При каком угле падения ε_в =отраженный свет полностью поляризован?

32.4. Угол Брюстера ε_в при падении света из воздуха на кристалл каменной соли равен 57°. Определить скорость света в этом кристал­ле.

32.5. Предельный угол ε`₁ полного отражения пучка света на гра­нице жидкости с воздухом равен 43°. Определить угол Брюстера ε_в для падения луча из воздуха на поверхность этой жидкости.

32.6. Пучок естественного света падает на стеклянную (n=1,6) призму (рис. 32.3). Определить двугранный угол θ призмы, если отраженный пучок максимально поляризован.

32.7. Алмазная призма находится в некоторой среде с показа­телем преломления n₁. Пучок естественного света падает на призму так, как это показано на рис. 32.4. Определить показатель прелом­ления n₁ среды, если отраженный пучок максимально поляризован.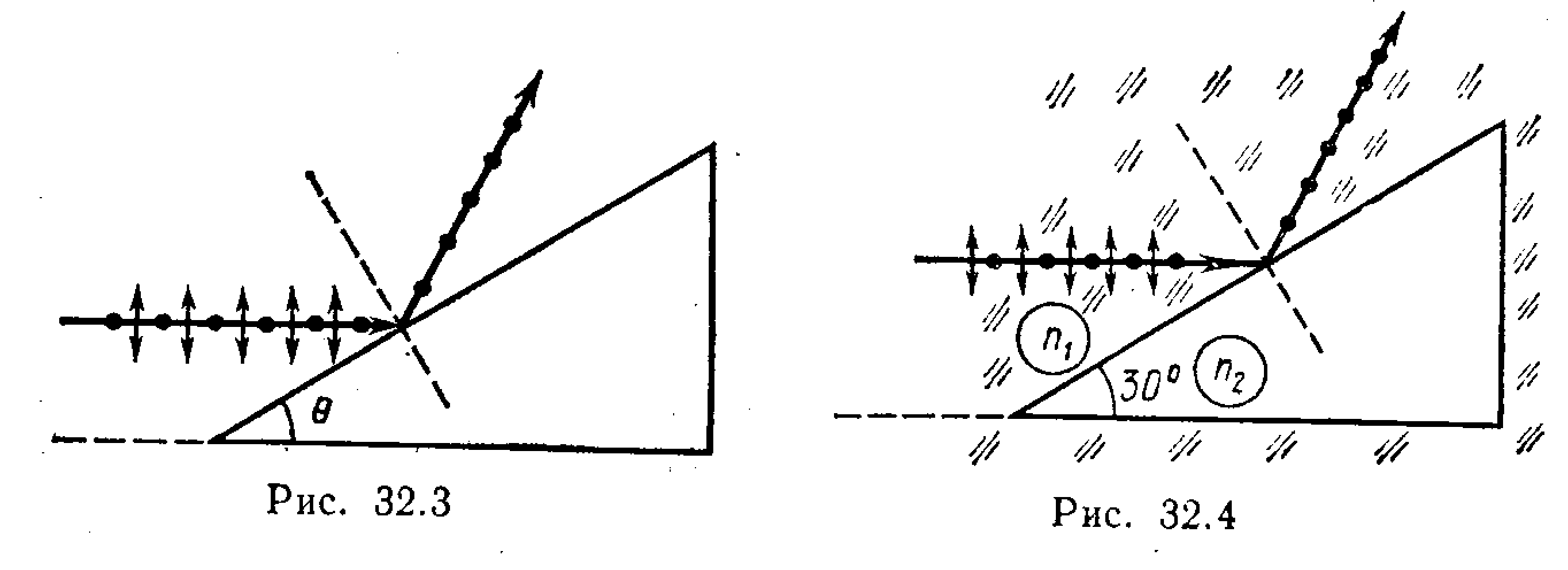





32.8. Параллельный пучок естественного света падает на сфери­ческую каплю воды. Найти угол α между отраженным и падающим пучками в точке А (рис. 32.5).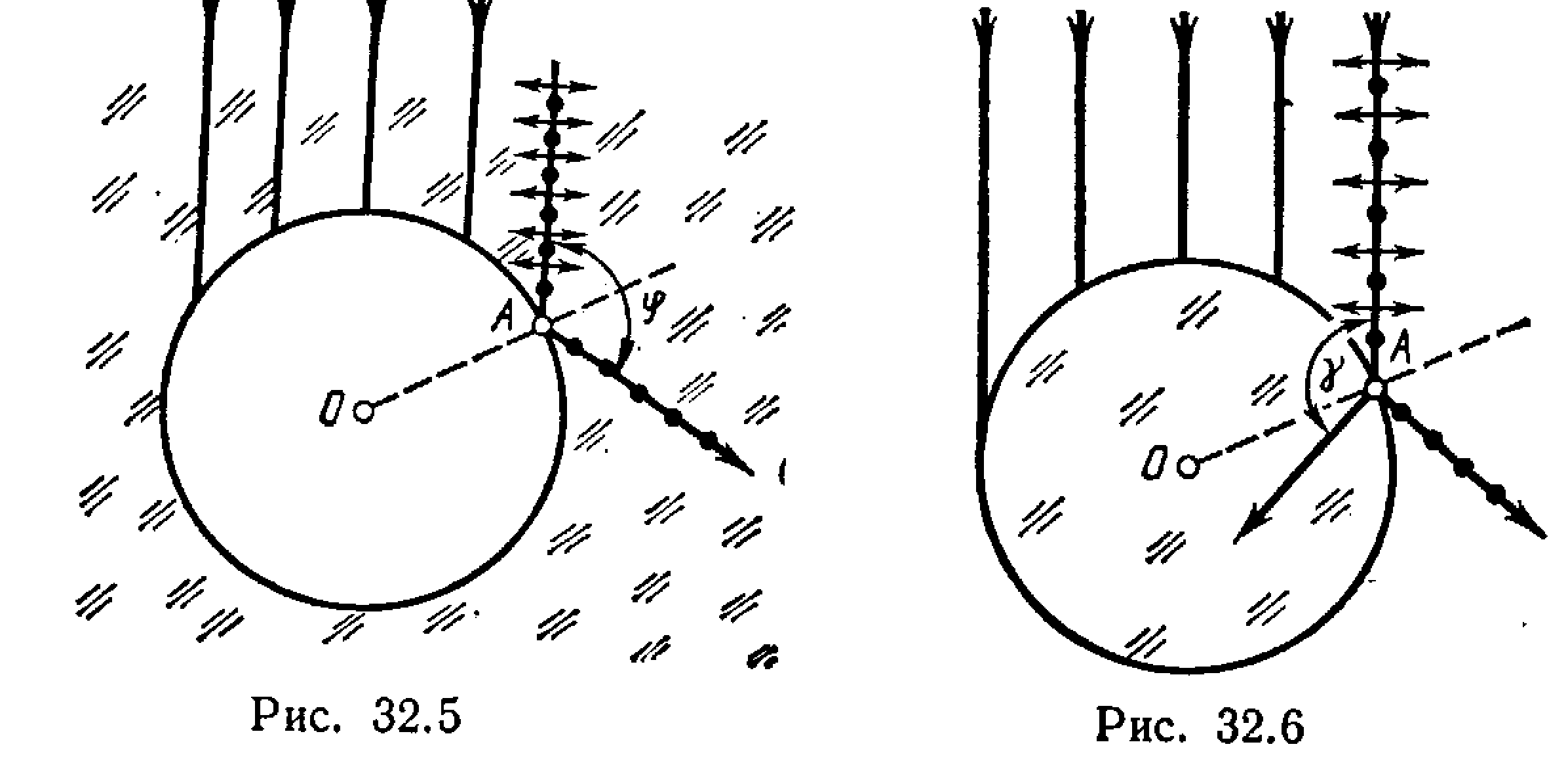





32.9. Пучок естественного света падает на стеклянный шар (п= 1,54). Найти угол γ между преломленным и падающим пучками в точке А (рис. 32.6).

32.10. Пучок естественного света падает на стеклянный шар, находящийся в воде. Найти угол φ между отраженным и падающим пучками в точке А (рис. 32.7). Показатель преломления n стекла принять равным 1,58.

32.11. Анализатор в k=2 раза уменьшает интенсивность света, приходящего к нему от поляризатора. Определить угол α между плоскостями пропускания поляризатора и анализатора. Потерями интенсивности света в анализаторе пренебречь.


32.12. Угол α между плоскостями пропускания поляризатора и анализатора равен 45°. Во сколько раз уменьшится интенсивность света, выходящего из анализатора, если угол увеличить до 60°?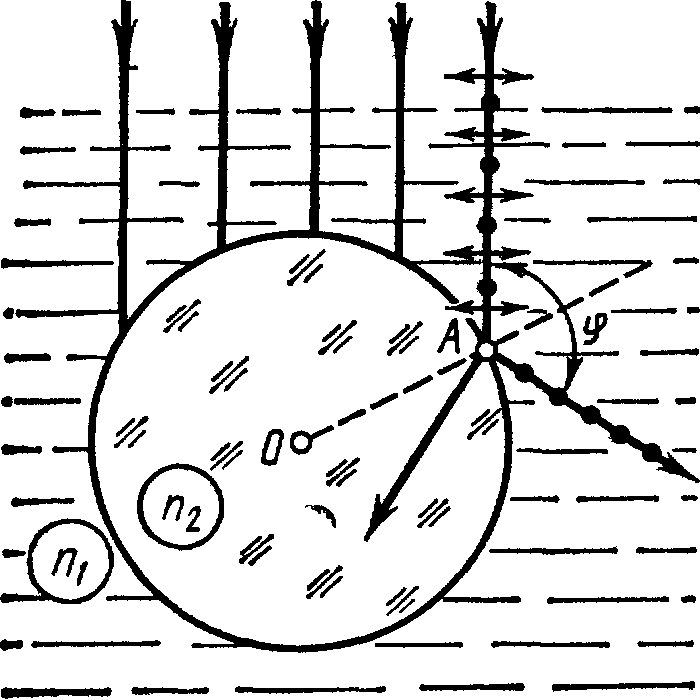



32.13. Во сколько раз ослабляется интенсивность света, прохо­дящего через два николя, плоскости пропускания которых образуют угол α=30°, если в каждом из николей в отдельности теряется 10 % интенсив­ности падающего на него света?


Рис. 32.7
32.14. В фотометре одновременно рассматривают две половины поля зрения: в одной видна эталонная све­тящаяся поверхность с яркостью L₁=5 ккд/м², в другой — испытуемая поверхность, свет от которой прохо­дит через два николя. Граница меж­ду обеими половинами поля зрения исчезает, если второй николь повер­нуть относительно первого на угол

α=45°. Найти яркость L₂ испытуемой поверхности, если извест­но, что в каждом из николей интенсивность падающего на него све­та уменьшается на 8 %.

Степень поляризации света

32.15. В частично-поляризованном свете амплитуда светового вектора, соответствующая максимальной интенсивности света, в n=2 раза больше амплитуды, соответствующей минимальной ин­тенсивности. Определить степень поляризации Р света.

32.16. Степень поляризации Р частично-поляризованного света

равна 0,5. Во сколько раз отличается максимальная интенсивность света, пропускаемого через анализатор, от минимальной?

32.17. На пути частично-поляризованного света, степень поля­ризации Р которого равна 0,6, поставили анализатор так, что интен­сивность света, прошедшего через него, стала максимальной. Во сколько раз уменьшится интенсивность света, если плоскость пропускания анализатора повернуть на угол α =30°?

32.18. На николь падает пучок частично-поляризованного света. При некотором положении николя интенсивность света, прошедшего через него, стала минимальной. Когда плоскость пропускания нико­ля повернули на угол β =45°, интенсивность света возросла в k = 1,5 раза. Определить степень поляризации Р света.

Вращение плоскости поляризации

32.19. Пластинку кварца толщиной d₁=2 мм, вырезанную перпен­дикулярно оптической оси, поместили между параллельными николями, в результате чего плоскость поляризации света повернулась на угол φ =53°. Определить толщину d₂ пластинки, при которой данный монохроматический свет не проходит через анализатор.

32.20. Никотин (чистая жидкость), содержащийся в стеклянной трубке длиной d=8 см, поворачивает плоскость поляризации жел­того света натрия на угол φ =137°. Плотность никотина ρ=1,01*10³ кг/м³. Определить удельное вращение [α] никотина.

32.21. Раствор глюкозы с массовой концентрацией C_i=280 кг/м³, содержащийся в стеклянной трубке, поворачивает плоскость поляри­зации монохроматического света, проходящего через этот раствор, на угол φ =32°. Определить массовую концентрацию С₂ глюкозы в другом растворе, налитом в трубку такой же длины, если он пово­рачивает плоскость поляризации на угол φ =24°.

32.22. Угол φ поворота плоскости поляризации желтого света натрия при прохождении через трубку с раствором сахара равен 40°. Длина трубки d=15 см. Удельное вращение [α] сахара равно 1.17*10^-2 рад*м³/(м*кг). Определить плотность ρ раствора.