конспект. Закон движения
 Скачать 71.23 Kb.
|
|
Часть 1. МЕХАНИКА Механическое движение состоит в изменении с течением времени взаимного расположения тел или их частей в пространстве. Глава 1. КИНЕМАТИКА 1.1 Кинематика материальной точки ипоступательногодвижениятвердоготела Положение тела в пространстве задается в трехмерной декартовой системе координат либо точкой , либо радиус-вектором. i→ 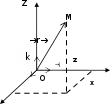 Y X y Рис. 1.1.
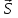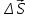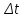Траектория – линия, вдоль которой движется материальная точка. Путь – длина траектории материальной точки. Перемещение материальной точки –вектор  , соединяющий ее начальное положение с конечным.Мгновенная скорость точки – отношение ее перемещения  за малый промежуток времени  к этому промежутку времени: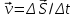 Вектор скорости 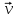 направлен по касательной к траектории движения.Единица скорости в СИ – м/с. Скорость задается аналогично 2 способами
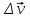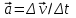Ускорение Ускорение точки – отношение изменения ее скорости  за малый промежуток времени: Единица ускорения в СИ – м/с2 . Мгновенное ускорение – называют величину , равн ую пределу 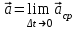 Ускорение как радиус–вектор 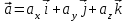 Из определения ускорения частные производные скорости – есть проекция скорости на ту ось. 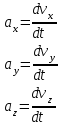 Модуль ускорения, можно найти сл образом 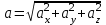 Рассмотрим движение вдоль криволинейной линии – криволинейное движение. Простейшиевидыдвиженияматериальнойточки Прямолинейноеравномерноедвижение. Прямолинейным равномерным движением называют движение материальной точки с постоянной по модулю и направлению скоростью: 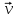= const.Скорость прямолинейного равномерного движения равна 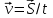 Перемещение при равномерном движении равно 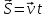 Уравнение равномерного движения x = 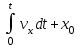 =x0 + vxtПрямолинейноеравнопеременноедвижение. Прямолинейным равнопеременным движением называют движение материальной точки с постоянной по модулю и направлению ускорением: 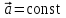 .Ускорение точки при равноускоренном движении равно 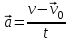 Скорость точки в момент t равна 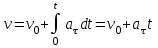 ,где 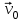 – начальная скорость.Перемещение точки при равноускоренном равно 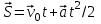 ,Выразив время t из формулы скорости и подставив в формулу перемещения, получим формулу 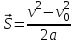 Уравнение равноускоренного движе–ния имеет вид: 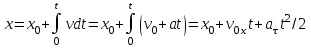 Равномерноедвижение по окружности - наиболее простой вид криволинейного движения. Равномерным движением по окружности называют движение материальной точки по окружности с постоянной по модулю скоростью: 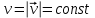 .Угловой скоростью ω называют величину, численно равную первой производной угла поворота φ (угла поворота) по времени t: ω = 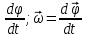 Угловая скорость в СИ измеряется в радианах в секунду (рад/с=1/с) Угловая скорость ω связана с модулем мгновенной скорости v и радиусом окружности R: 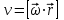 Период (Т) – это время одного полного оборота. Частота ( n) – число оборотов в еди–ницу времени. Они связаны с угловой скорос–тью: ω = 2π/T = 2πn При равномерном движении по окружности ускорение точки всегда направлено к центру окружности и равно по величине (центростремительное ускорение) 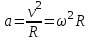 .Угловое ускорение 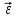 – мера быстроты изменения угловой скорости.  |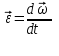
,
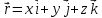
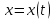
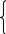
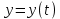
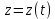
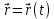
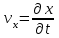
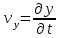
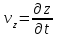
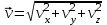
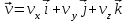