шпоры. Закон фильтрации вид зависимости между вектором скорости фильтрации и полем давления, которое вызывает фильтрацию. Есть 2 закона линейный (линейная зависимость) и нелинейный
 Скачать 69.5 Kb.
|
|
1 Закон фильтрации – вид зависимости между вектором скорости фильтрации и полем давления, которое вызывает фильтрацию. Есть 2 закона: линейный (линейная зависимость) и нелинейный. Рассмотрим опыт Дарси (линейный закон) производилась фильтрация жидкости через песок. h1 –напор в начале трубки. h2 –в конце. L – Длина образца, kф – коэф. фильтрации (коэф. пропорциональности) Установим формулу закон Дарси (линейный закон фильтрации) Q= - kф*ΔH/L*F – закон Дарси (разделим на F) Q/F= - kф*ΔH/L; Q/F= υ; i=ΔH/L; υ = - kф*i, гд i – гидравлический уклон kф – скорость фильтрации при единичном гидравлическом уклоне. (м2/с) Если происходит очень малое изменение давления, то  Минус обусловлен тем, что перепад давления в противоположную сторону движения жидкости. нелинейный закон фильтрации. – зависимость между gradP и скоростью фильтрации нелинейная (возможно для неньютоновских жидкостей, при проявлении сил инерции). Общий вид:  с –скоростной коэффициент; n –показатель закона фильтрации (от 1 до 2). при n=2 – закон Краснопольского. 2 Существуют две основные группы причин отклонения от закона Дарси:1) отклонения, связанные с проявлением инерционных сил при высоких скоростях фильтрации (верхняя граница применимости закона Дарси); 2) отклонения при достаточно малых скоростях фильтрации, вызванные проявлением неньютоновских реологических свойств жидкости, ее взаимодействием с твердым скелетом пористой среды (нижняя граница применимости закона Дарси). Многочисленные экспериментальные исследования были направлены на вывод универсальной зависимости (по аналогии с трубной гидравликой) коэффициента гидравлического сопротивления к от числа Рейнольдса. Однако вследствие различной структуры и состава пористых сред получить такую универсальную зависимость не удается. Первая количественная оценка верхней границы применимости закона Дарси была дана более 60 лет назад Н. Н. Павловским, который, опираясь на результаты Ч. Слихтера, полученные для модели идеального грунта, и полагая характерный размер d равным эффективному диаметру dэф , вывел следующую формулу для числа Рейнольдса:  спользовав эту формулу и данные экспериментов, Н. Н. Павловский установил, что критическое значение числа Рейнольдса находится в пределах  при значениях числа Рейнольдса Re>Reкр линейный закон Дарси перестает быть справедливым. Отклонения от закона Дарси при малых скоростях фильтрации. При весьма малых скоростях потока сила вязкого трения пренебрежимо мала, тогда как сила межфазного взаимодействия действия остается при этом конечной величиной, поскольку она не зависит от скорости и определяется только свойствами контактирующих фаз. В результате такого взаимодействия нефть, содержащая поверхностно-активные компоненты, в присутствии пористого тела с развитой поверхностью образует устойчивые коллоидные растворы (студнеобразные пленки), частично или полностью перекрывающие поры. Чтобы началось движение, нужно разрушить эту структуру, приложив некоторый перепад давления. Нижняя граница применимости закона Дарси связана с проявлением неньютоновских свойств фильтрующихся флюидов, что характеризуется повышенным содержанием в нефти высокомолекулярных компонентов (смол, асфальтенов, парафина и др.). В этом случае предлагается нелинейный закон фильтрации неньютоновских жидкостей, в основе которого лежит модель фильтрации с предельным градиентом, в виде:  где γ – предельный (начальный) градиент давления, по достижении которого начинается движение жидкости; при меньших значениях градиента движение отсутствует. 3 Приток жидкости в скважины происходит под действием разницы между пластовым давлением и давлением на забое скважины. Так, как движение жидкости в пласте происходит с весьма малыми скоростями, то оно подчиняется линейному закону фильтрации — закону Дарси. Для установившегося плоскорадиального потока однородной жидкости по закону Дарси дебит скважины можно определить по формуле  где Q — дебит скважины (объем жидкости, поступающей на забой скважины в единицу времени); k — проницаемость пласта; h — толщина пласта; Рпл — пластовое давление; Рз — забойное давление в скважине;  — вязкость жидкости; RK и rс — радиусы контура питания и скважины, соответственно.а. Формула (4.8), называемая формулой Дюпюи, широко используется для расчета дебита гидродинамически совершенных скважин (скважины с открытым забоем, вскрывшие пласты на всю толщину (а)). б. Гидродинамически несовершенная по степени вскрытия - Если скважина имеет открытый забой, но вскрыла пласт не на всю толщину (б). в. Гидродинамически несовершенная по характеру вскрытия - Скважина, вскрывшая пласт на всю толщину, но соединяющиеся с пластом посредством перфорации ( в). г. Есть скважины и с двойным видом несовершенства — как по степени, так и по характеру вскрытия (г). Вблизи ствола гидродинамической несовершенной скважины происходит искажение плоскорадиальной формы потока и возникают дополнительные фильтрационные сопротивления потоку жидкости. 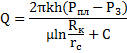 Приток жидкости в скважины происходит под действием разницы между пластовым давлением и давлением на забое скважины. Так, как движение жидкости в пласте происходит с весьма малыми скоростями, то оно подчиняется линейному закону фильтрации — закону Дарси. Для установившегося плоскорадиального потока однородной жидкости по закону Дарси дебит скважины можно определить по формуле где Q — дебит скважины (объем жидкости, поступающей на забой скважины в единицу времени); k — проницаемость пласта; h — толщина пласта; Рпл — пластовое давление; Рз — забойное давление в скважине; — вязкость жидкости; RK и rс — радиусы контура питания и скважины, соответственно.а. Формула (4.8), называемая формулой Дюпюи, широко используется для расчета дебита гидродинамически совершенных скважин (скважины с открытым забоем, вскрывшие пласты на всю толщину (а)). б. Гидродинамически несовершенная по степени вскрытия - Если скважина имеет открытый забой, но вскрыла пласт не на всю толщину (б). в. Гидродинамически несовершенная по характеру вскрытия - Скважина, вскрывшая пласт на всю толщину, но соединяющиеся с пластом посредством перфорации ( в). г. Есть скважины и с двойным видом несовершенства — как по степени, так и по характеру вскрытия (г). Вблизи ствола гидродинамической несовершенной скважины происходит искажение плоскорадиальной формы потока и возникают дополнительные фильтрационные сопротивления потоку жидкости. 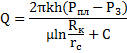|