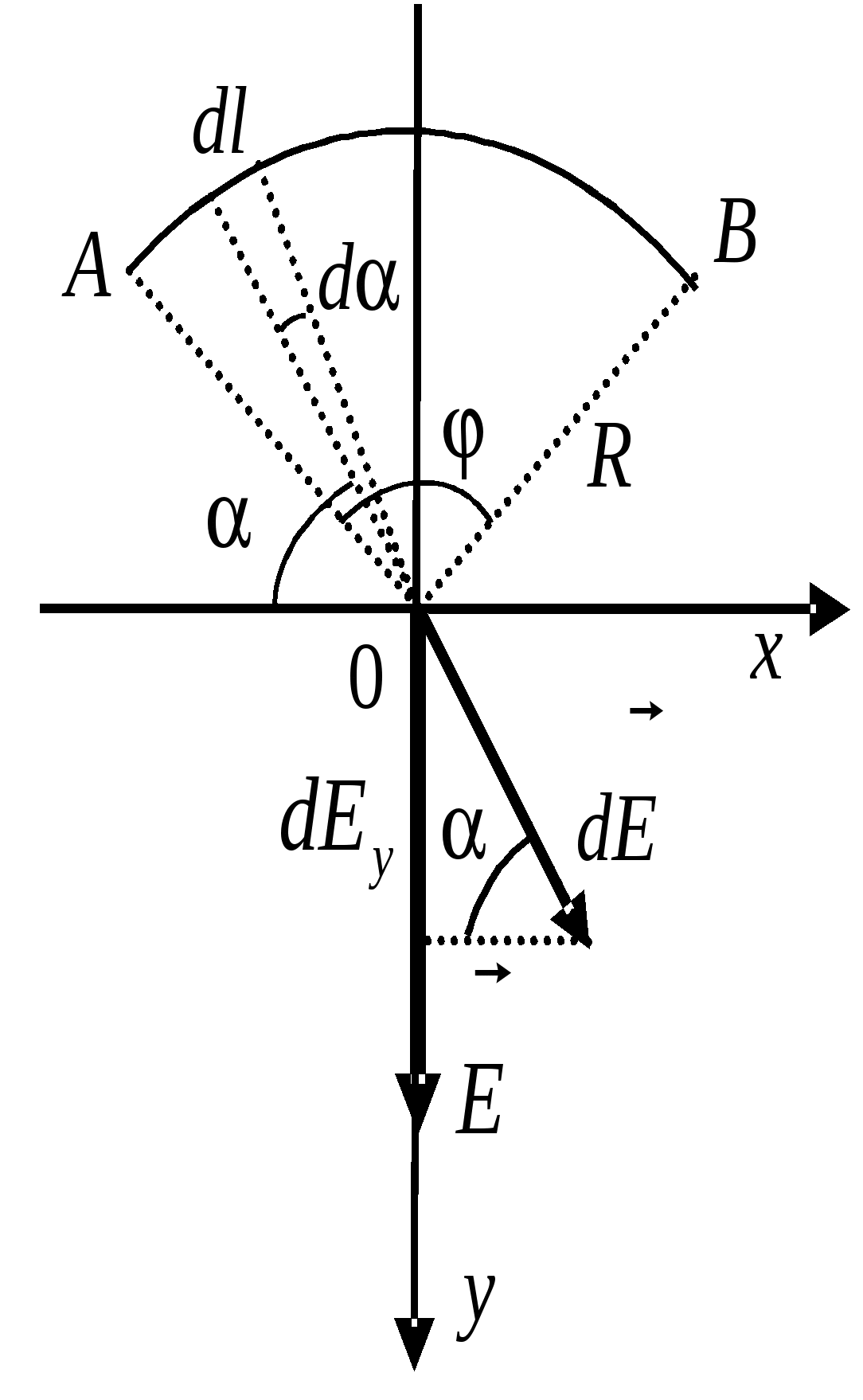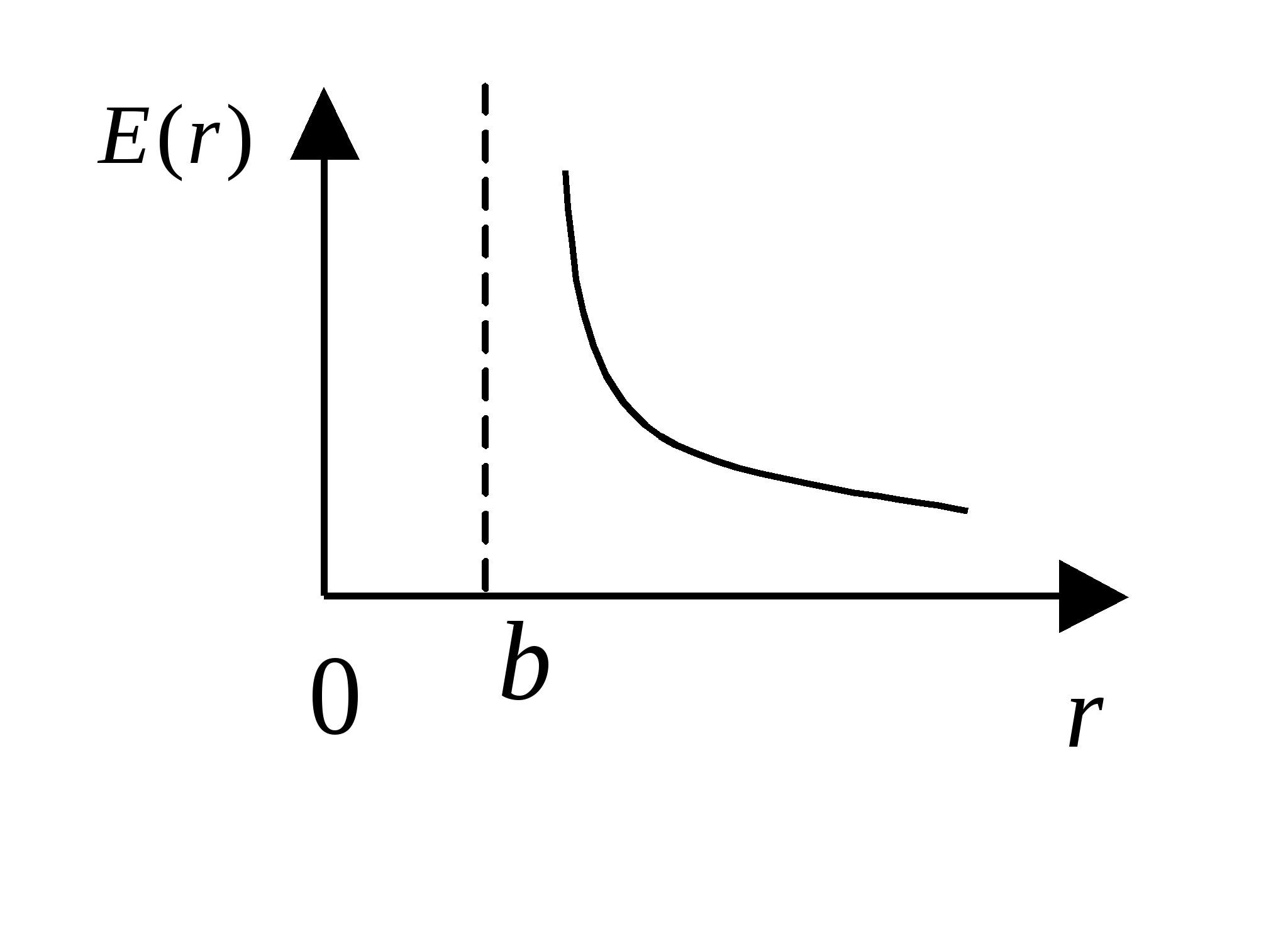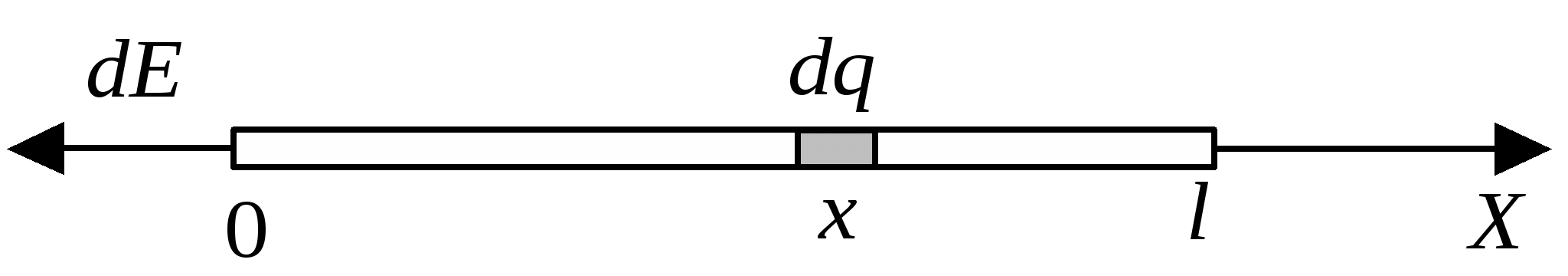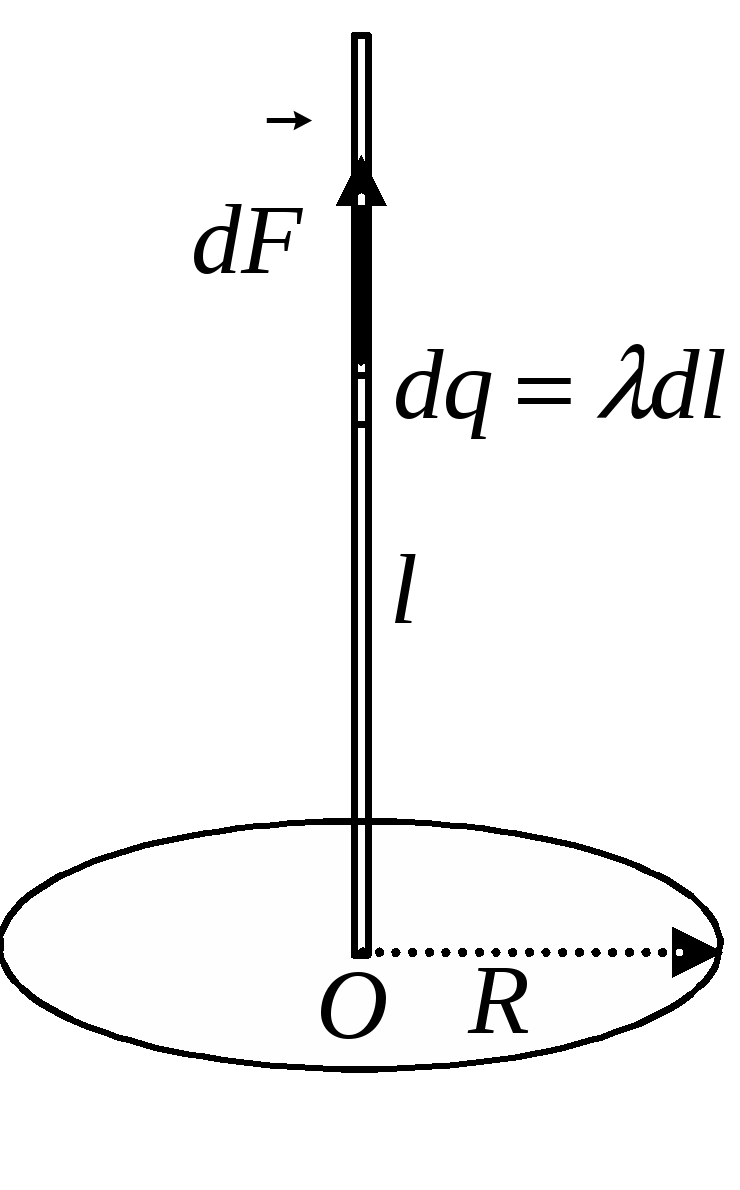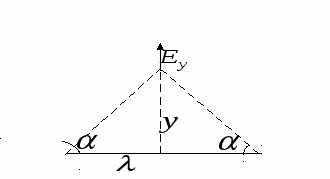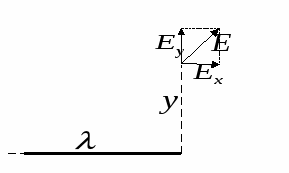Закон Кулона. Напряженность электрического поля. Принцип суперпозиции (примеры решения задач) Закон Кулона. Электростатическое поле системы точечных зарядов Пример 1

• Название: Закон Кулона. Напряженность электрического поля. Принцип суперпозиции (примеры решения задач) Закон Кулона. Электростатическое поле системы точечных зарядов Пример 1
• Дата: 21.02.2019
• Размер: 1.31 Mb.
• Имя файла: 2_1Primeryreshenia.doc
• Тип: Закон; #68516

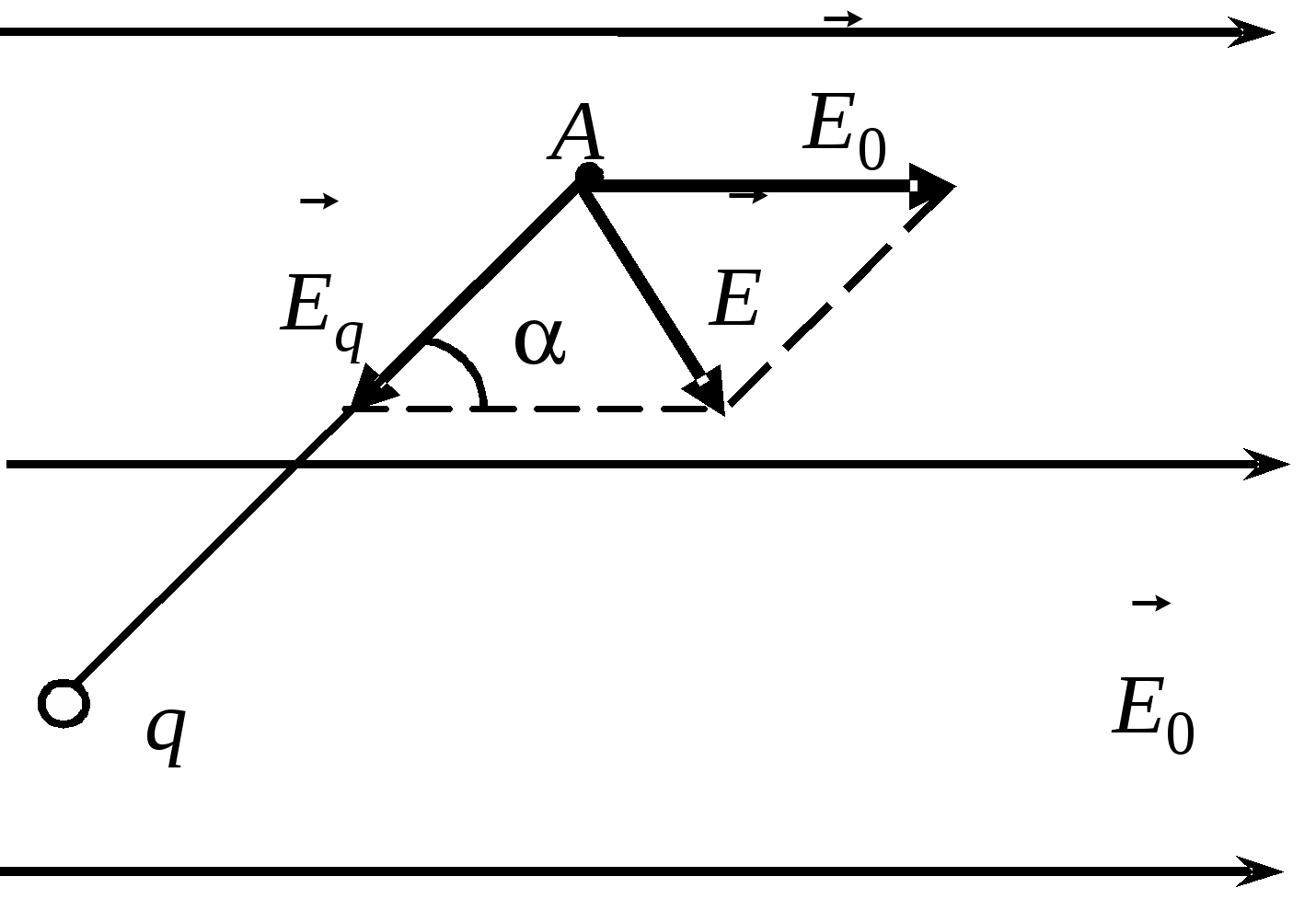
1. Закон Кулона. Напряженность электрического поля.

Принцип суперпозиции

(примеры решения задач)

Закон Кулона. Электростатическое поле системы точечных зарядов

Пример 1.1

В однородном электрическом поле напряженностью закреплен точечный отрицательный заряд . В точке A, положение которой определяется расстоянием и углом (см. рис.), модуль вектора напряженности результирующего электрического поля . Определите угол .

Решениe.

Напряженность результирующего поля согласно принципу суперпозиции равна

,

гденапряженность поля, создаваемого точечным зарядом q в точке А (рис.)

.

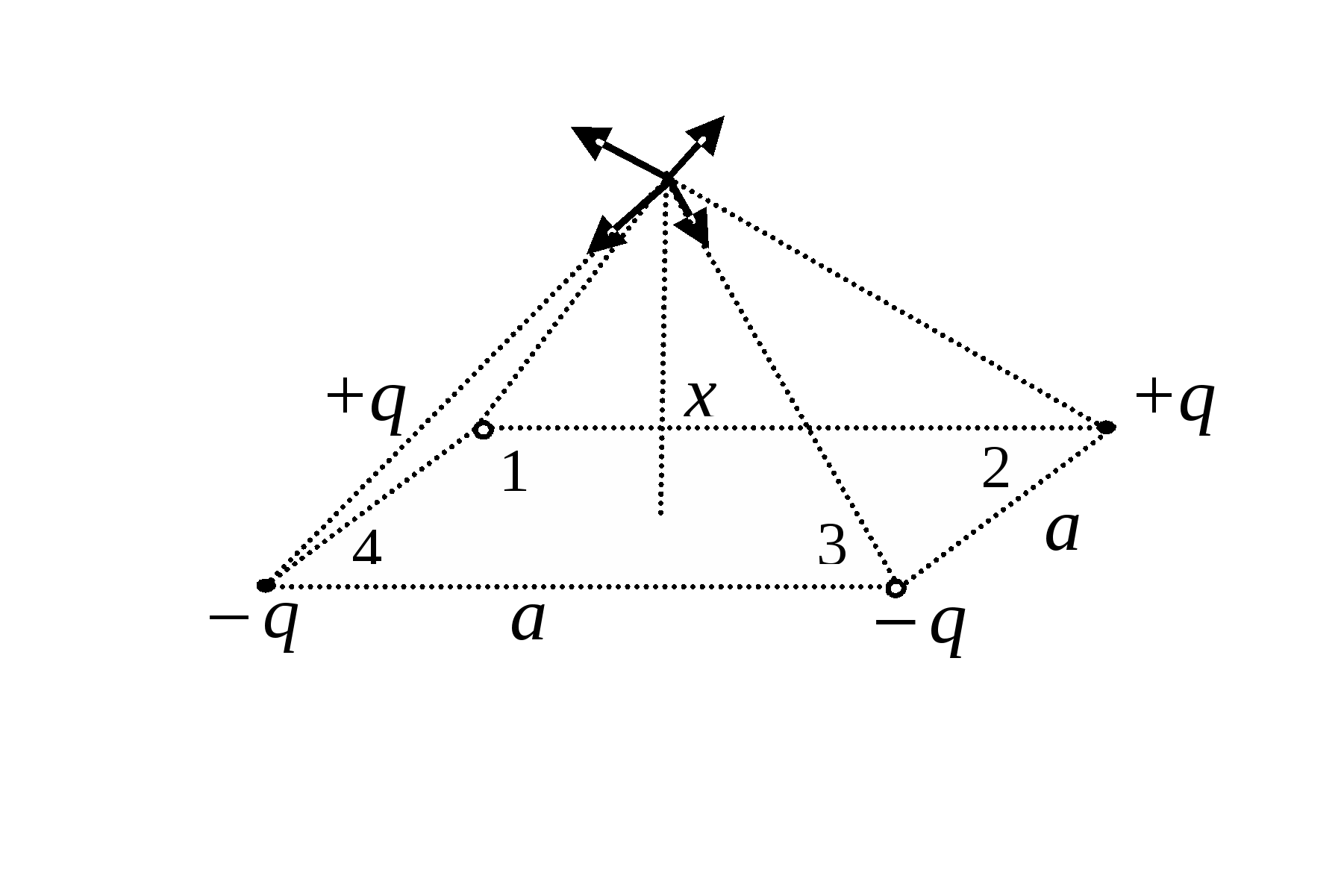
По теореме косинусов

.

Учитывая, что по условию задачи, получим для искомого угла :

.

Пример 1.2

Два одинаковых небольших металлических шарика с зарядами и , находящихся на расстоянии l = 0,2 м друг от друга притягиваются с силой H. После того как шарики привели в соприкосновение и опять развели на то же расстояние l, они стали отталкиваться с силой Н. Найдите и .

Решение.

Так как в начале шарики притягивались, то их заряды противоположны по знаку и по закону Кулона

(1)

После того, как шарики были приведены в соприкосновение, заряды перераспределяются, и на каждом из шариков заряд, согласно закону сохранения заряда, становится равным Поэтому они стали взаимодействовать с силой

(2)

Уравнения (1) и (2), дают систему уравнений для неизвестных и





решив которую, находим искомые заряды

Кл,

Кл.

Заметим, что в соответствии с симметрией задачи возможны и
такие значения зарядов: Кл,  Кл.

Пример 1.3

В вершинах квадрата, со стороной а, помещены четыре зарядаq (см. рис.).

Найдите напряженность электрического поля на перпендикуляре, восстановленном из центра квадрата, как функцию его длины x.

Решение.

Из принципа суперпозиции полей, результирующее поле, создаваемое зарядами, равно:



=, где .

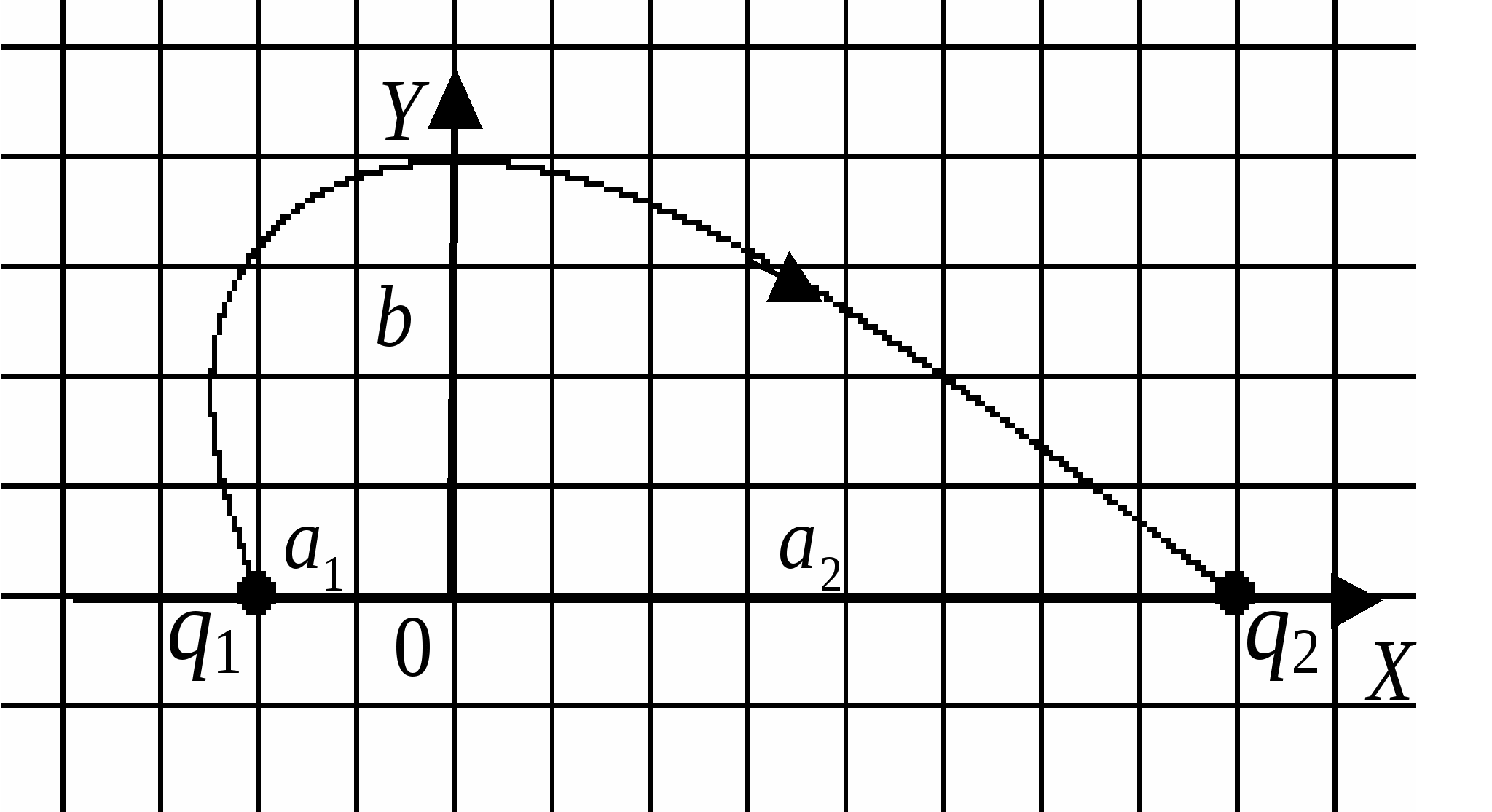
Задача сводится к суммированию четырех равных по величине, но разных по направлению векторов . Найдем векторную сумму полей положительного и отрицательного зарядов 1 и 3. Из подобия треугольников на рисунке получим:

, т.е. .

Аналогично, складывая поля 2-го и 4-го зарядов найдем . Для сложения векторов и учтем их равенство по величине и взаимную перпендикулярность. По теореме Пифагора, получим

.

Пример 1.4

На рисунке изображена одна из линий напряженности электрического поля двух неподвижных точечных зарядов и . Известно, что нКл. Определите .


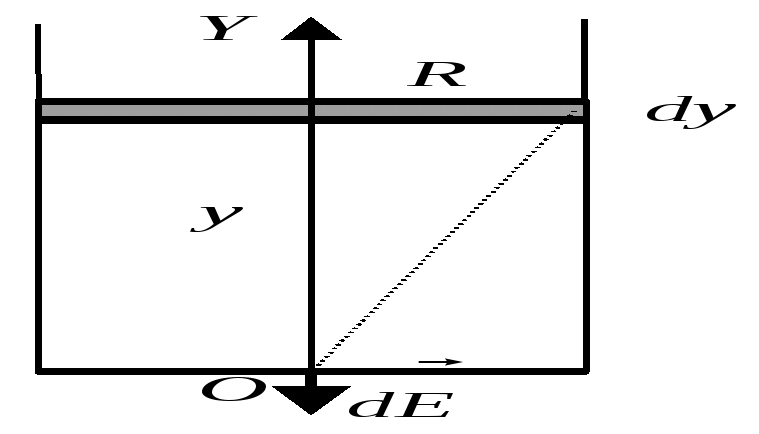
Решение.

Введем систему координат, выбрав ее, как показано на рисунке, т.е. ось x проходит через заряды, а ось y проходит через «вершину» линии поля. Так как вектор поля направлен по касательной к линии поля, то в точке «вершины» Е_y = 0. По принципу суперпозиции для поля в этой точке имеем:

, где

,

.

После подстановки и преобразований, найдем, взяв значения геометрических параметров из рисунка в условии задачи a₁ =2, a₂ = 8, b = 4: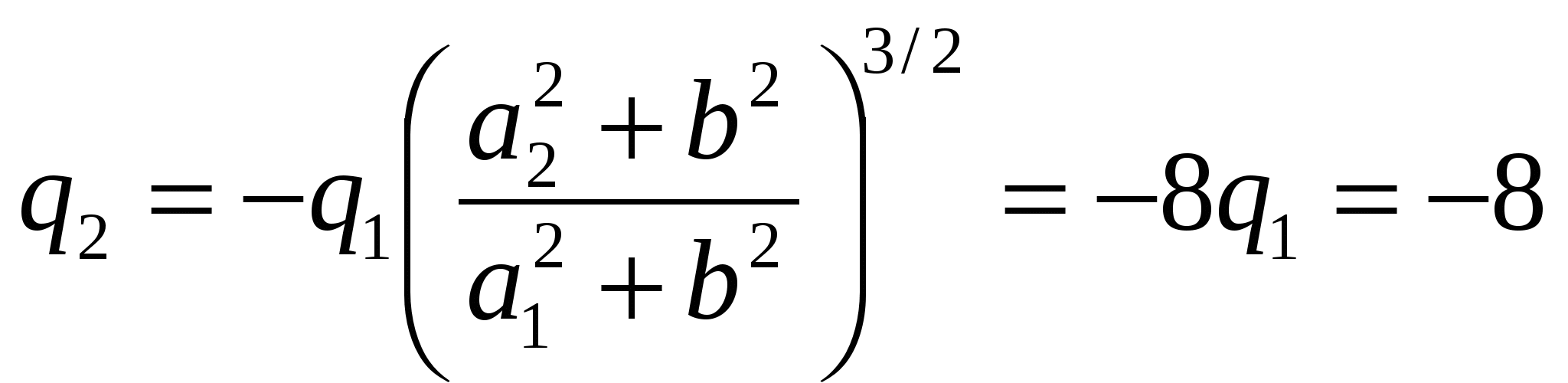

нКл.
Электростатическое поле заряженных тел (непрерывное распределение зарядов)

Пример 1.5

На единицу длины тонкого однородно заряженного стержня АВ, имеющего форму дуги окружности радиуса R с центром в точке О, приходится заряд . Найдите модуль напряженности электрического поля в точке О, если угол АОВ равен .

Решение.

Выберем оси координат так, чтобы начало координат совпадало с точкой О, а ось у была симметрично расположена относительно концов дуги АВ (рис.).

Разобьем стержень на элементарные участки длины dl с зарядом , который можно рассматривать как точечный.

Найдем напряженность поля, создаваемого зарядом этого элементарного участка стержня в точке 0:

,

где - радиус вектор, направленный от элемента dl к точке, напряженность которой вычисляется. Напряженность результирующего поля найдем, воспользовавшись принципом суперпозиции. В силу симметрии результирующее поле будет направлено вдоль оси у (рис.). Запишем выражение для проекции :

.

Приведем правую часть последнего уравнения к одной переменной интегрирования – углу (учитывая, что )

.

Проинтегрировав левую часть полученного уравнения от до E, а правую от до , найдем модуль напряженности электрического поля, создаваемого в точке О дугой АВ:

.
Рассмотрим специальные случаи использования формулы для расчета поля, создаваемого частью дуги окружности в ее центре :

а) Модуль напряженности электрического поля, создаваемого 1/4 части дуги окружности радиуса R в ее центре:

.

б) Модуль напряженности электрического поля, создаваемого тонким полукольцом радиуса R в его центре:

.

в) Модуль напряженности электрического поля, создаваемого тонким кольцом радиуса R в его центре:

.

г) Модуль напряженности электрического поля в центре тонкого кольца радиуса R, если половины этого кольца заряжены разноименными зарядами с линейными плотностями заряда и .

Напряженность электрического поля, создаваемого каждой из половинок равна:

,

.

С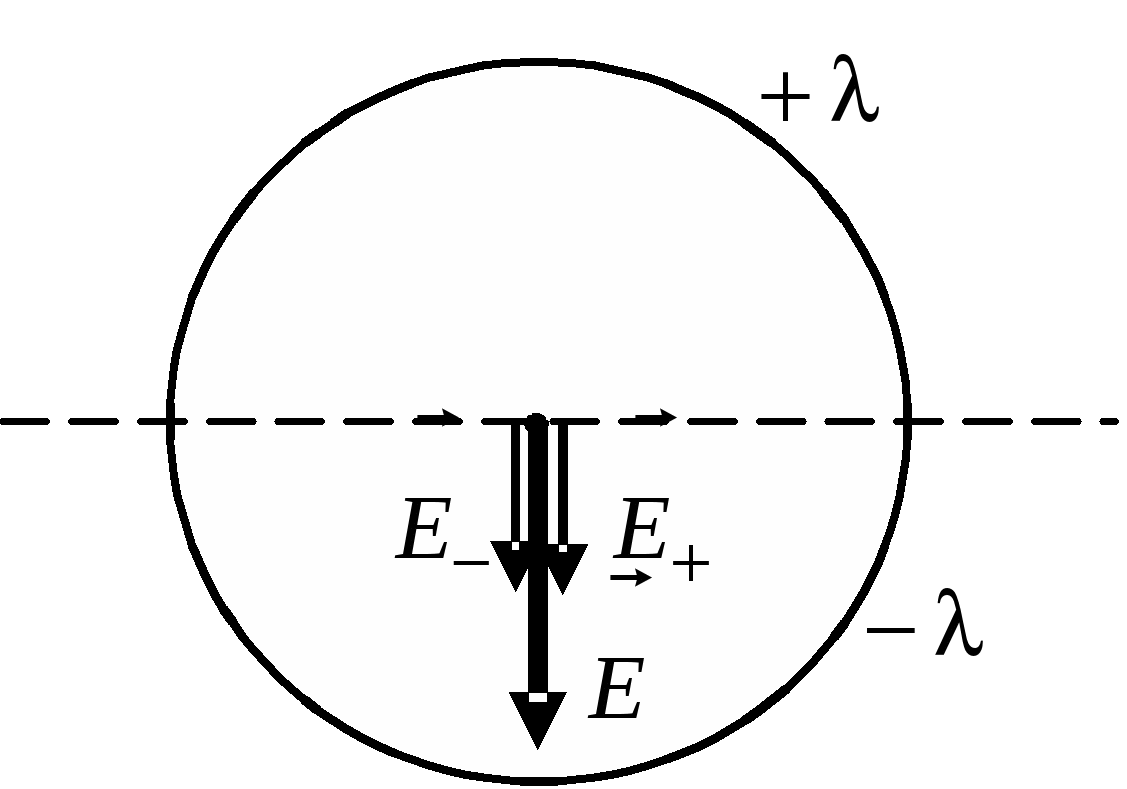огласно принципу суперпозиции найдем результирующее поле в центре

.

Из рисунка видно, что направления векторов и совпадают, поэтому результирующее поле в центре такого кольца равно

.

Пример 1.6

Найти модуль и направление напряженности поля в центре кольца радиуса а, по которому однородно распределен заряд q>0, а в кольце сделана прорезь шириной b << a.

Решение.

Рассмотрим кольцо без прорези. Тогда в силу симметрии в центре кольца поле равно нулю. С другой стороны это поле является суперпозицией поля кольца с прорезью и поле заряда в прорези(рис.):

, откуда




Поле , в силу малости прорези, описывается полем точечного заряда величиной q_b=qb/(2πa-b)qb/2πa, имеет величину и направлено от прорези. Поэтому и направлено от центра кольца к прорези.

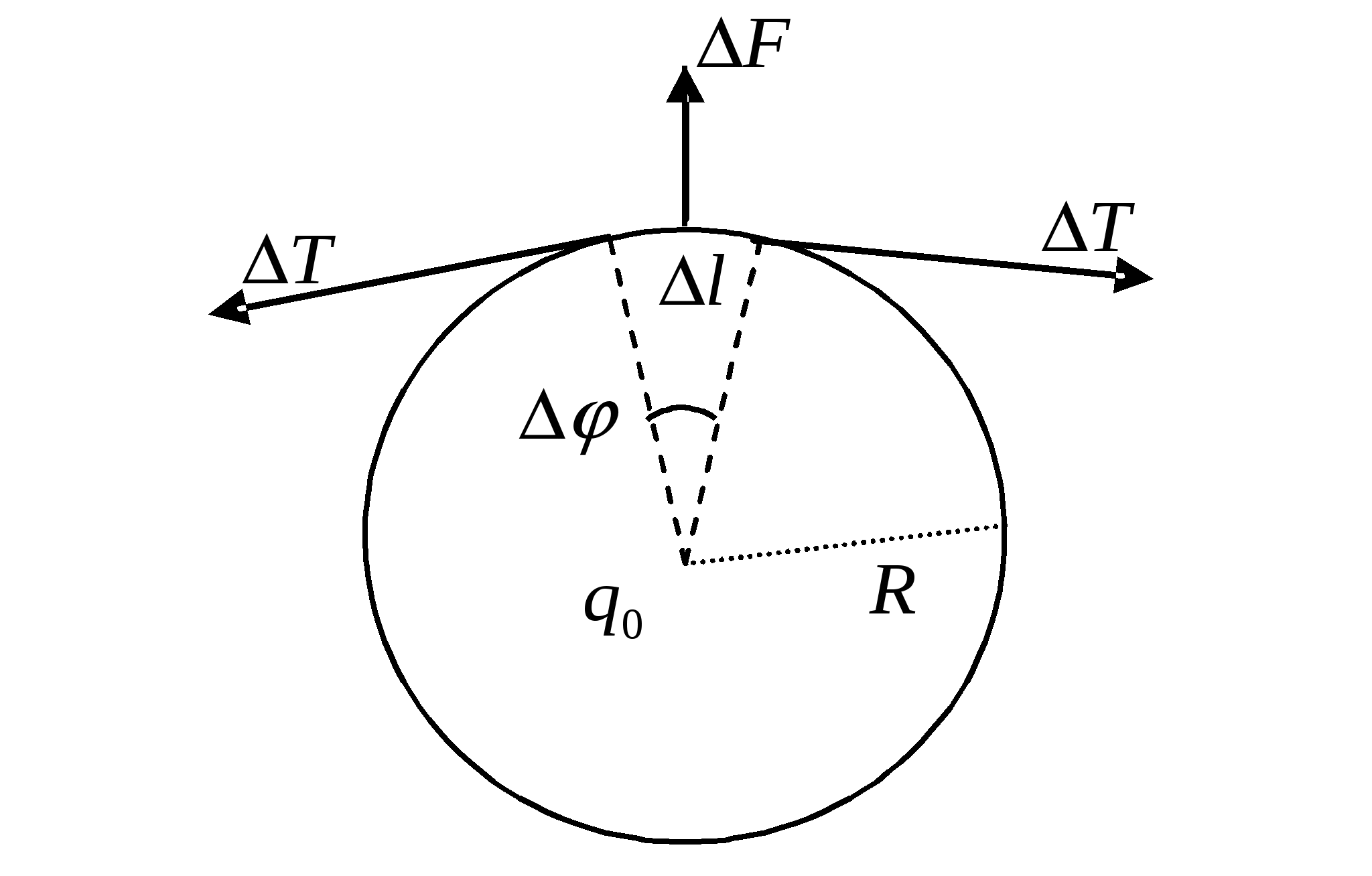
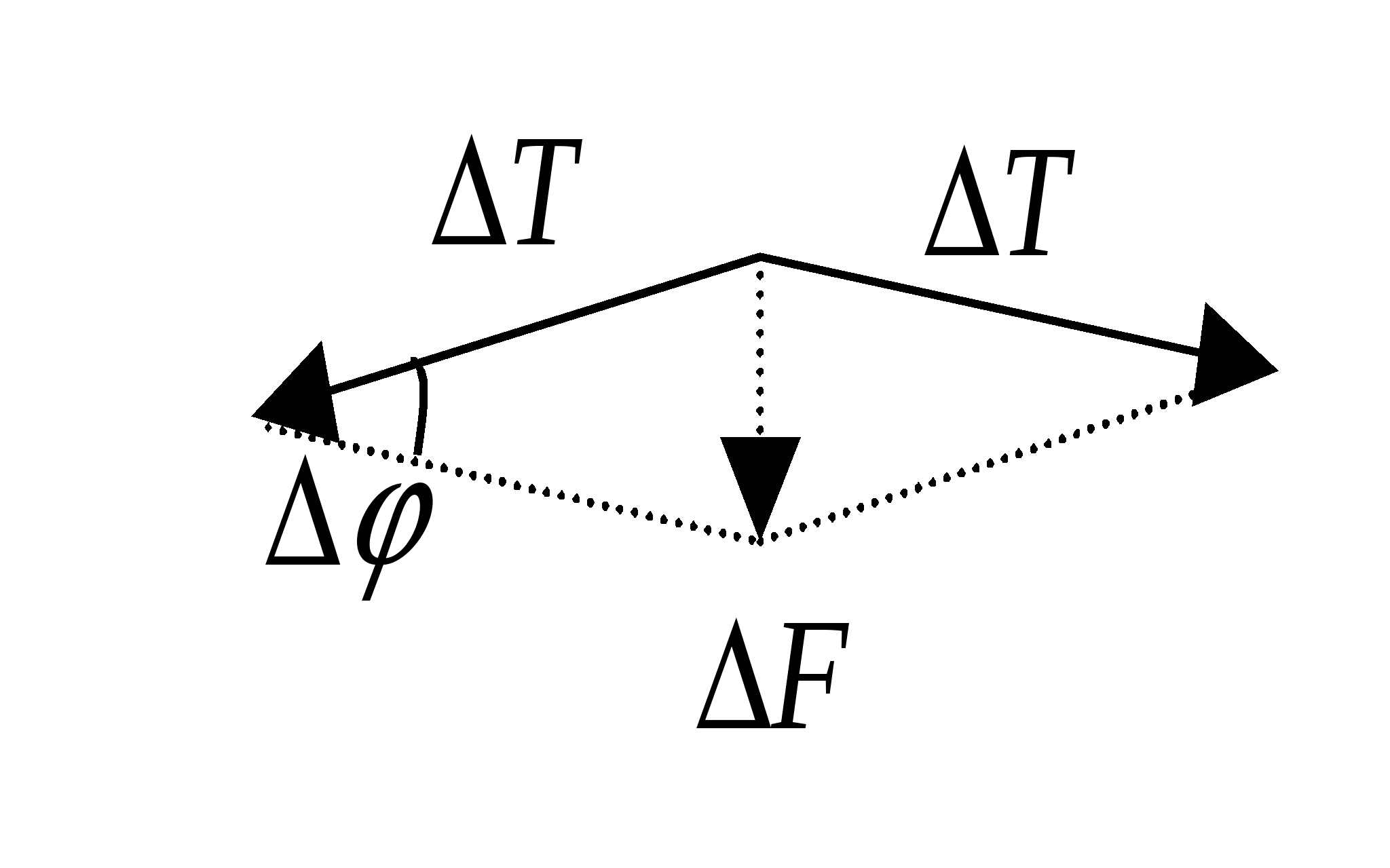
Пример 1.7

Тонкое проволочное кольцо радиуса мм имеет однородно распределенный заряд мк Кл. Каково будет приращение силы, растягивающей проволоку, если в центре кольца поместить точечный заряд мк Кл?
Решение.

Выберем на кольце элементарную дугу с зарядом . По закону Кулона сила взаимодействия зарядов и равна , где ( - линейная плотность заряда).


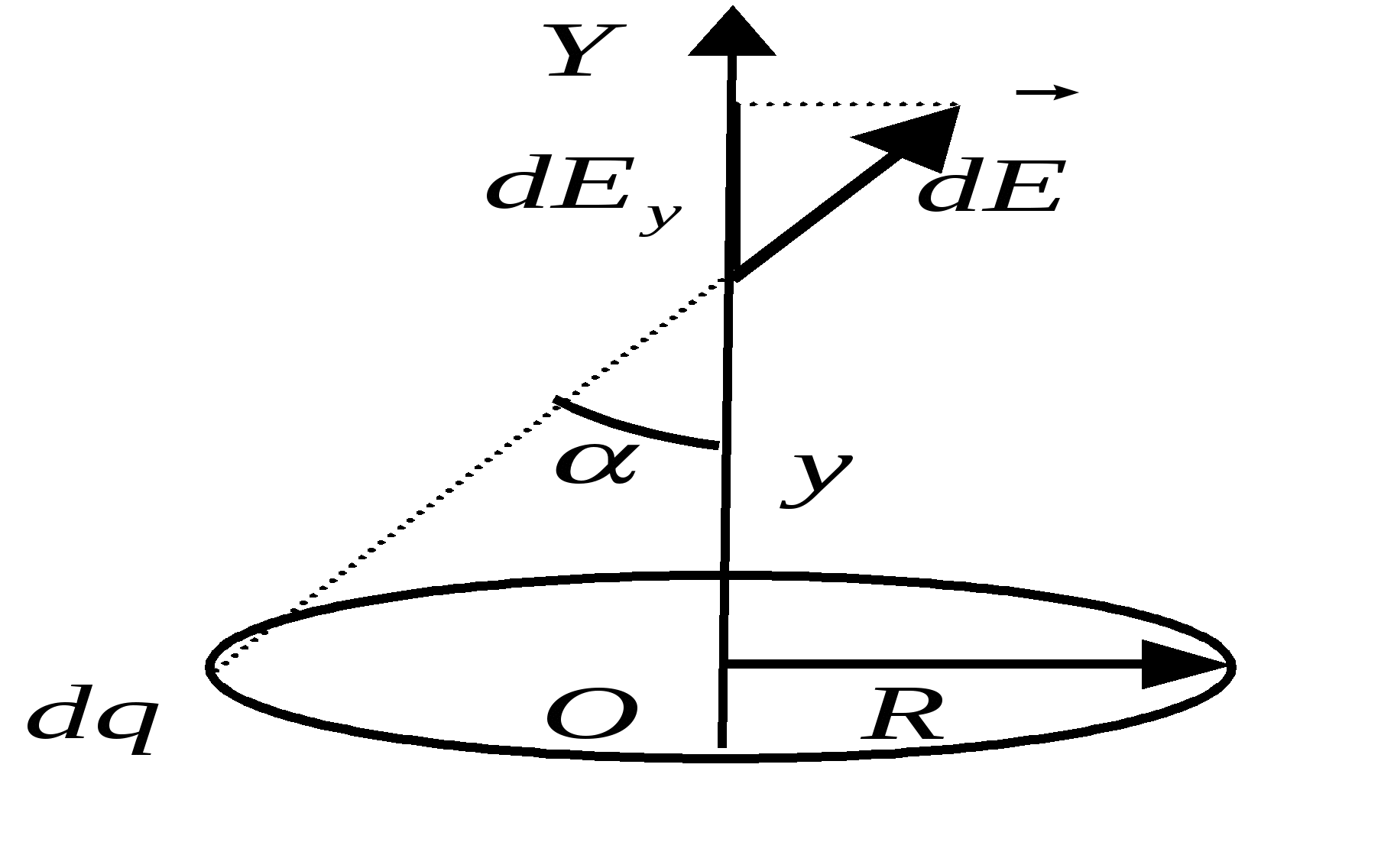
В равновесии величина силы равна равнодействующей приращения сил, растягивающих проволоку .

Из подобия треугольников (см. рисунок) имеем:



где .

Выражая ,получим:

.

Пример 1.8

Кольцо радиуса из тонкой проволоки имеет однородно распределенный заряд . Найдите модуль напряженности электрического поля на оси кольца как функцию расстояния до его центра. Исследуйте при .

Решение.

Разобьем заряд кольца на бесконечно малые элементы с зарядами , которые можно рассматривать как точечные. На оси кольца выберем произвольную точку с координатой . Заряд создаст в этой точке напряженность поля , направление которого показано на рисунке, а его величина равна:

.

Напряженность результирующего поля найдем, воспользовавшись принципом суперпозиции. В силу симметрии результирующее поле будет направлено вдоль оси (см. рисунок). Поэтому , где:




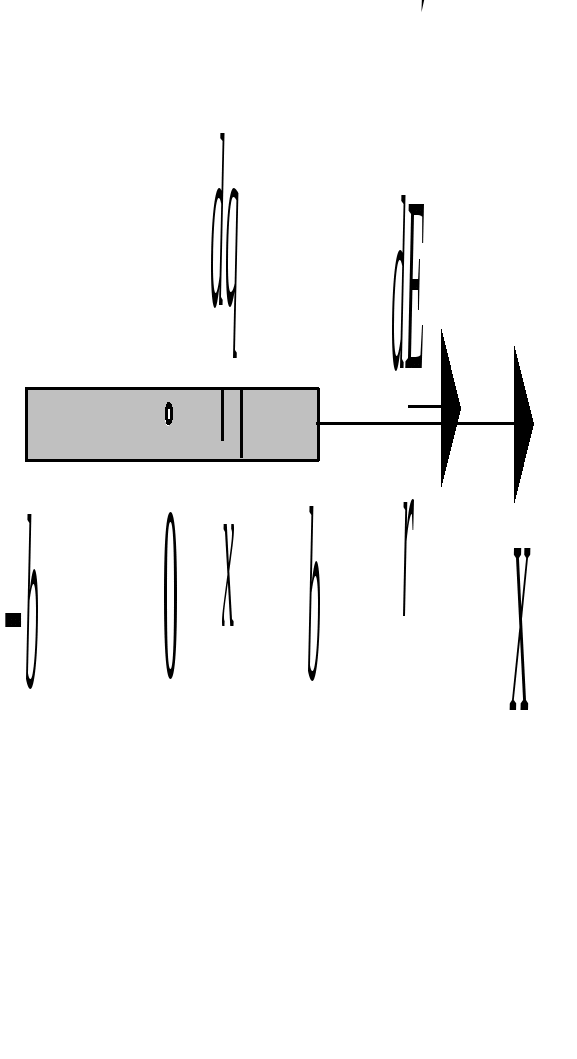
Учитывая, что , получим:

.

Суммируя вклады всех элементов кольца, найдем для проекции результирующего поля:

.

Рассмотрим напряженность поля на больших расстояниях .

,

т.е. на больших расстояниях система ведет себя как точечный заряд.

График представлен на рисунке.



Точки, в которых напряженность поля принимает максимальные значения, имеют координаты.

Пример 1.9

Находящийся в вакууме тонкий прямой стержень длины заряжен однородно зарядом . Найдите модуль напряженности электрического поля как функцию расстояния rот цента стержня до точки прямой, совпадающей с осью стержня . Исследуйте полученное выражение при .

Решение.

Выделим на стержне элементарный заряд , находящийся на участке стержня , на расстоянии от начала координатной оси. В произвольной точке на оси стержня с координатой заряд создает напряженность поля величиной:




Применяя принцип суперпозиции для нахождения напряженности поля, создаваемого стержнем в искомой точке, получим: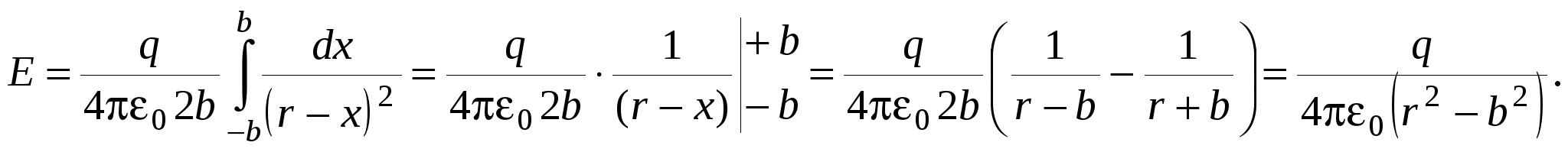



График напряженности поля, создаваемого заряженным стержнем на его оси представлен на рисунке.

При напряженность поля , т.е. на больших расстояниях поле стержня ведет себя как поле точечного заряда q, помещенного в центр стержня.

Пример 1.10

Тонкий прямой стержень заряжен с линейной плотностью , где длина стержня, расстояние от конца стержня, положительная постоянная. Найдите модуль напряженности электрического поля при .

Решение.

Разобьем заряженный стержень на бесконечно малые элементы с зарядами

Каждый заряд создает в точке напряженность поля :



Все вектора сонаправлены. Поэтому для нахождения напряженности поля , создаваемого всем заряженным стержнем в точке , применим принцип суперпозиции, суммируя величины элементарных векторов:

Пример 1.11

Система состоит из тонкого заряженного проволочного кольца радиуса и очень длинной однородно заряженной нити, расположенной по оси кольца так, что один из ее концов совпадает с центром кольца. Последнее имеет заряд . На единицу длины нити приходится заряд . Найдите силу, с которой кольцо действует на нить.

Решение.

Разобьем нить на элементарные участки длины dl с зарядом , каждый из которых можно рассматривать как точечный. На каждый точечный заряд кольцо действует с силой

,

где - напряженность электрического поля, создаваемого заряженным кольцом на оси на расстоянии от центра. Согласно результату примера 1.7

.

Подставим в выражение для величину поля и, проинтегрировав левую часть полученного уравнения от до F , а правую от 0 до , найдем силу взаимодействия кольца и нити:
.

Учитывая, что 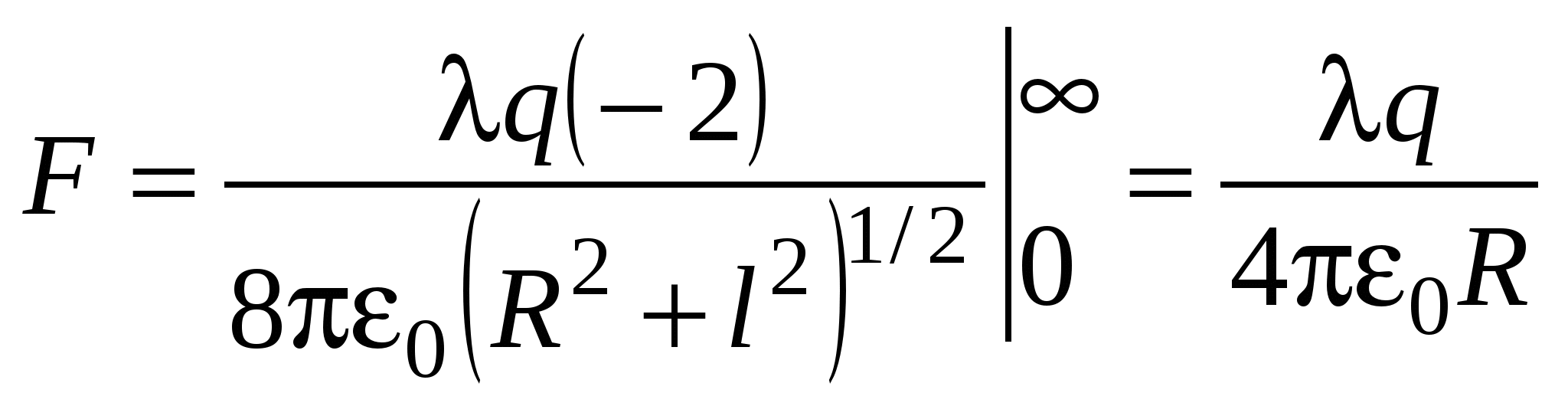, приведем последнее выражение к виду удобному для интегрирования и найдем искомую величину

.

Пример 1.12

Полубесконечный круглый цилиндр радиуса заряжен однородно по поверхности так, что на единицу его длины приходится заряд .

Найдите напряженность электрического поля в центре основания цилиндра.
Решение.

Представим, что цилиндр состоит из набора круглых тонких колец ширины каждое. Точка находится на оси этих колец.

Воспользуемся формулой для напряженности поля на оси равномерно заряженного кольца (пример1.7):



где – заряд одного кольца. Тогда



Все напряженности 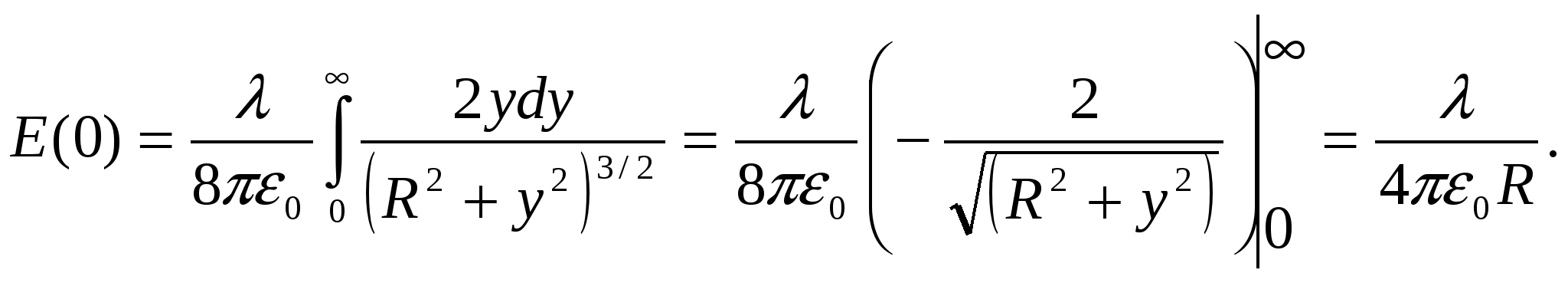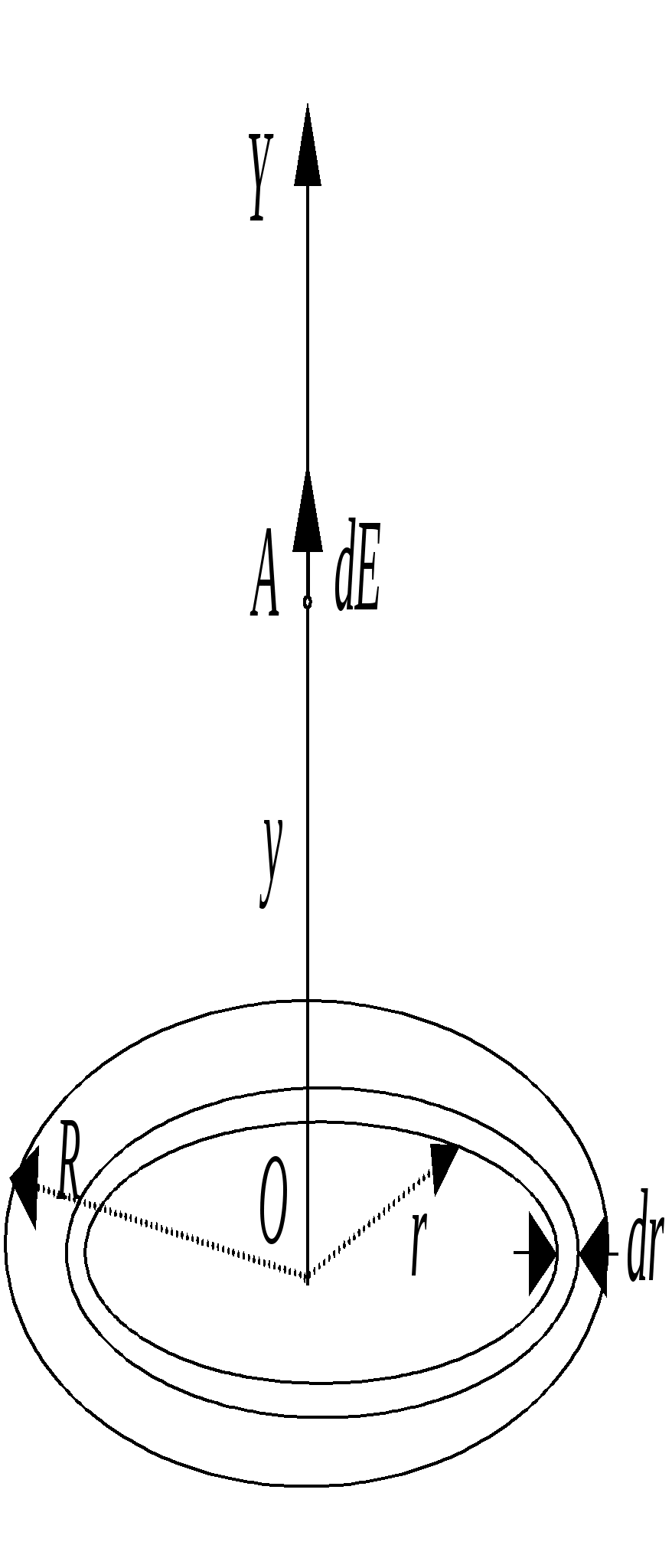в точке , создаваемые кольцами направлены одинаково (против оси ). По принципу суперпозиции, имеем:

Пример 1.13

Круглая тонкая пластинка радиуса однородно заряжена с поверхностной плотностью .

Найдите модуль напряженности электрического поля на оси пластинки, как функцию расстояния от ее центра. Рассмотрите предельные случаи и .

Решение.

Представим круглую пластинку в виде набора узких концентрических колец радиуса и ширины (см. рис.).

Заряд одного такого элементарного кольца равен:

,

где площадь этого кольца.

Используя формулу для напряженности поля на оси кольца из примера 1.7., запишем напряженность поля в произвольной точке 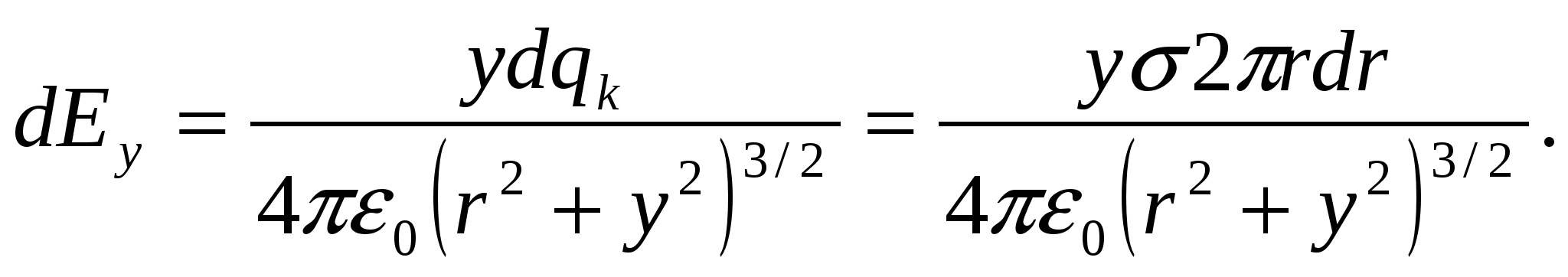с координатой :



Векторы 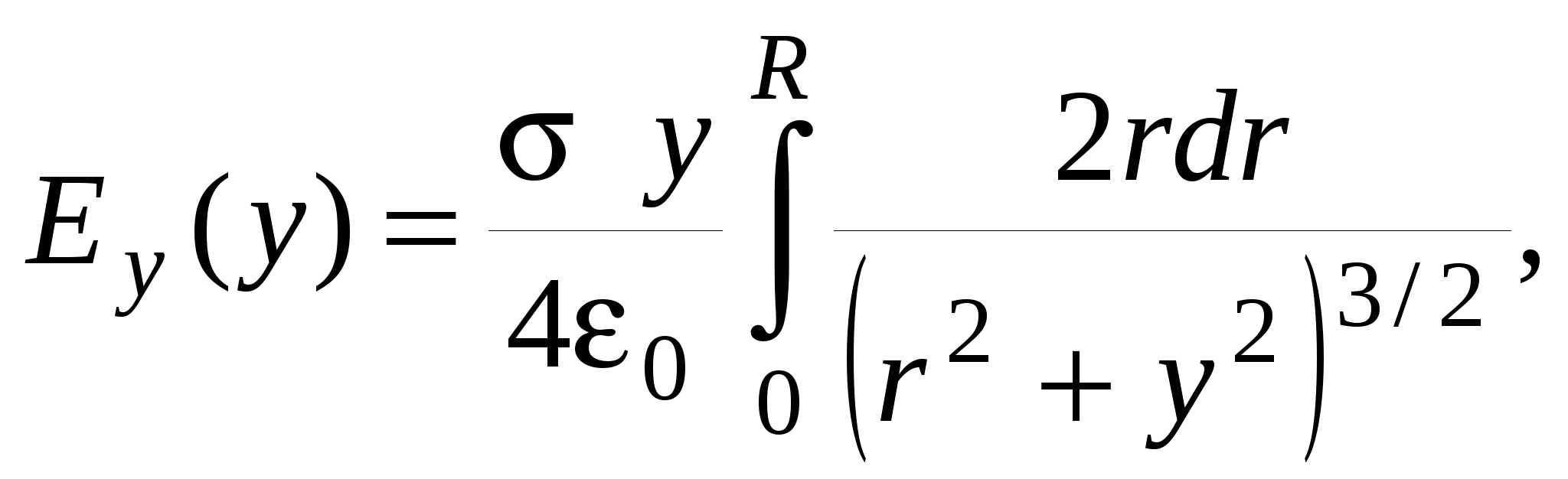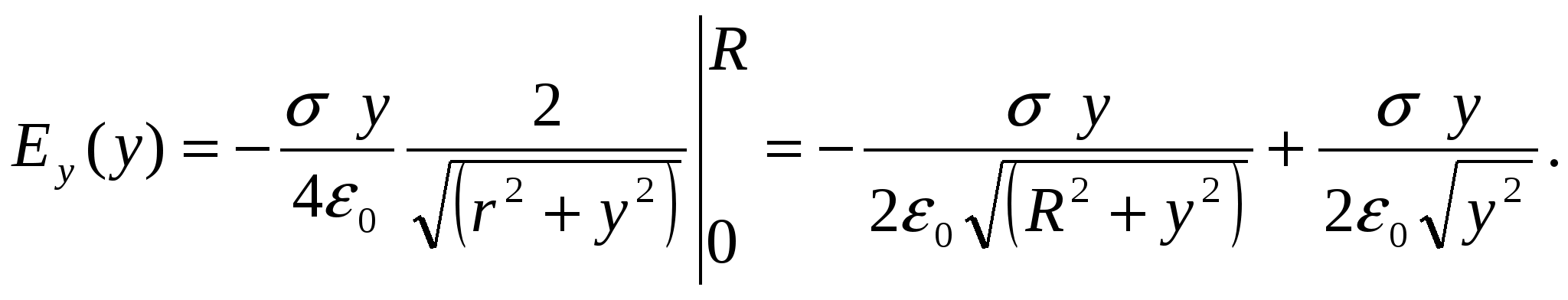направлены одинаково для всех колец пластинки (по оси , так как заряд пластинки положительный). Применив принцип суперпозиции для напряженности, найдем :





Построим график зависимости :



Рассмотрим предельные случаи:

1) при 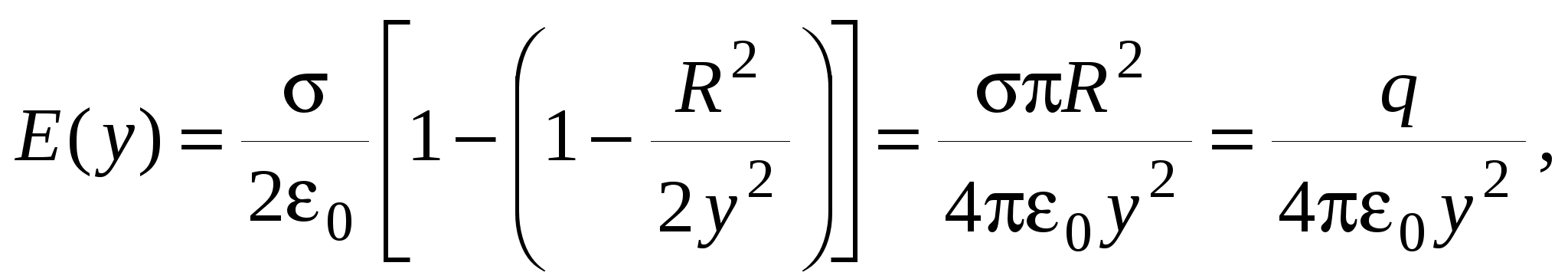- что соответствует полю бесконечной равномерно заряженной плоскости;

2) при , учитывая что , поле пластинки можно привести к виду:



то есть на больших расстояниях поле круглой пластинки соответствует полю точечного заряда, помещенного в ее центр.
П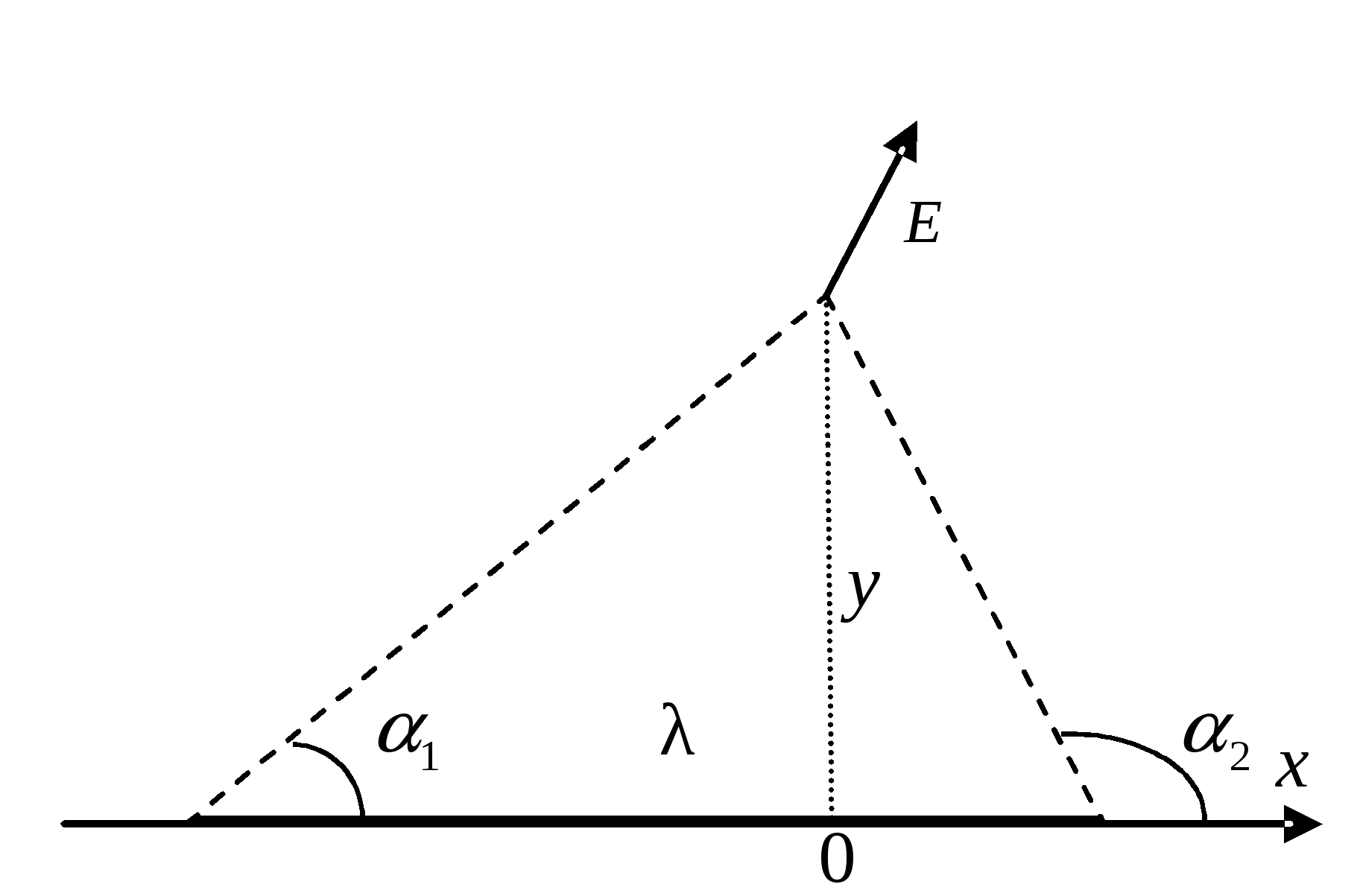ример 1.14

Найти напряженность электрического поля, созданного отрезком тонкой, однородно заряженной с линейной плотностью нити в точке наблюдения c координатами , (см. рис.). Углы с осью x, под которыми видна точка наблюдения из концов отрезка , и расстояние y - известны.

Решение.

Вклад в напряженность поля от элемента отрезка dx равен 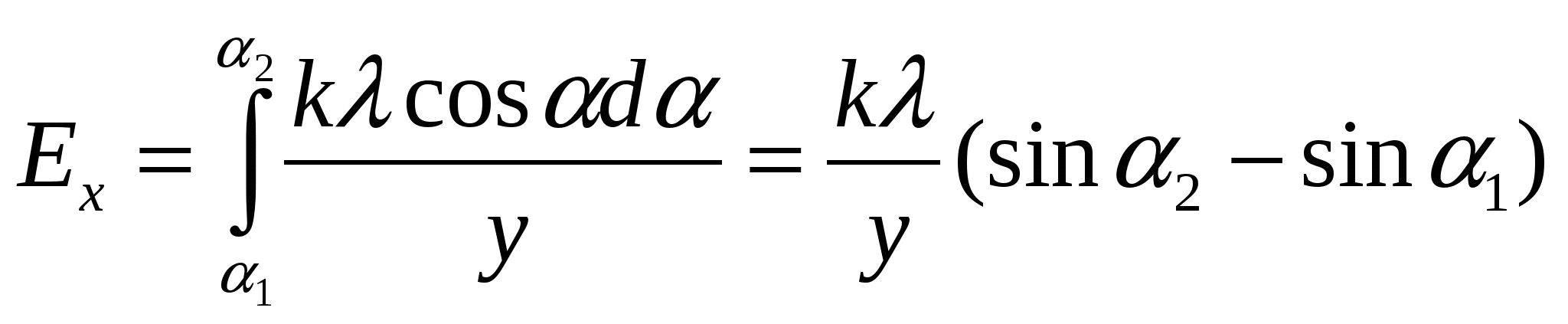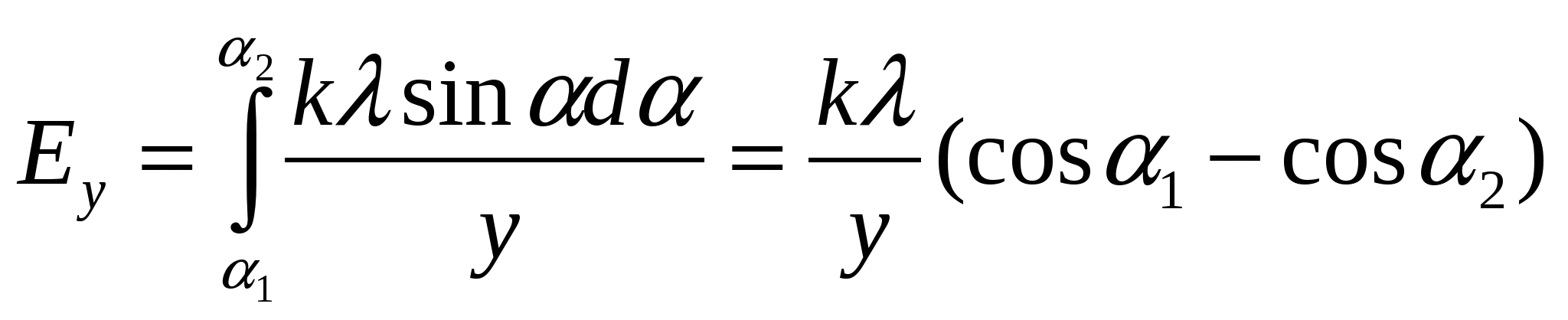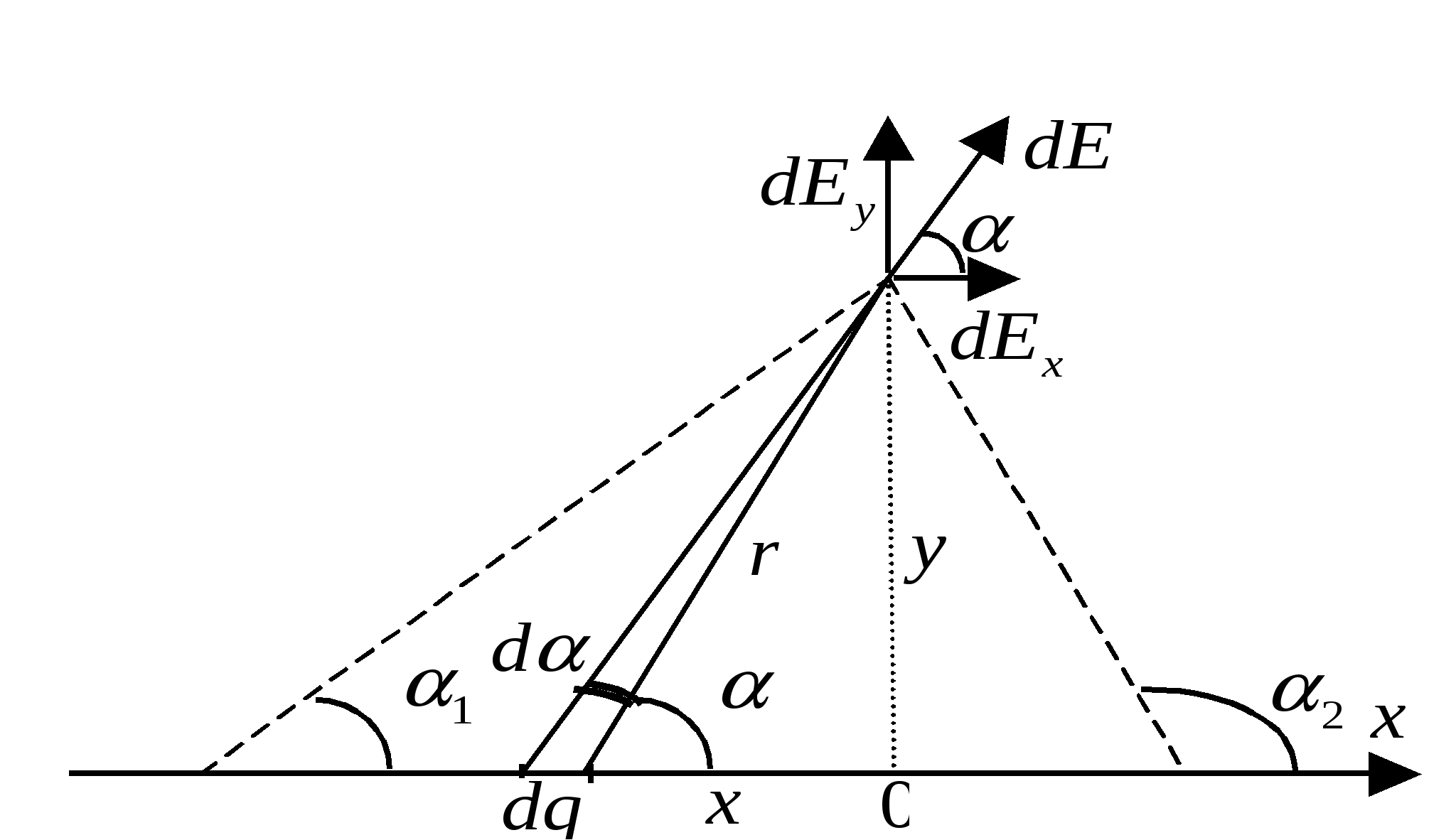. Поля от разных элементов отрезка отличаются как величиной, так и направлением. Поэтому для нахождения результирующего поля проинтегрируем проекции элементарных полей и . Для удобства интегрирования выразим переменные величины r и xчерез угол по соотношениям (см.рис.) и , . При этом и для проекций E_x и E_y получим:

,
Полученные формулы включают в себя все результаты расчета полей однородно заряженных отрезков. Приведем наиболее часто используемые:

Поле на перпендикуляре, проведенном из середины отрезка:



,



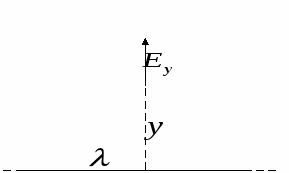
Поле бесконечного отрезка:

, ,



Поле полубесконечного отрезка в точках плоскости перпендикулярной отрезку и проходящей через его торец:

,


Пример 1.15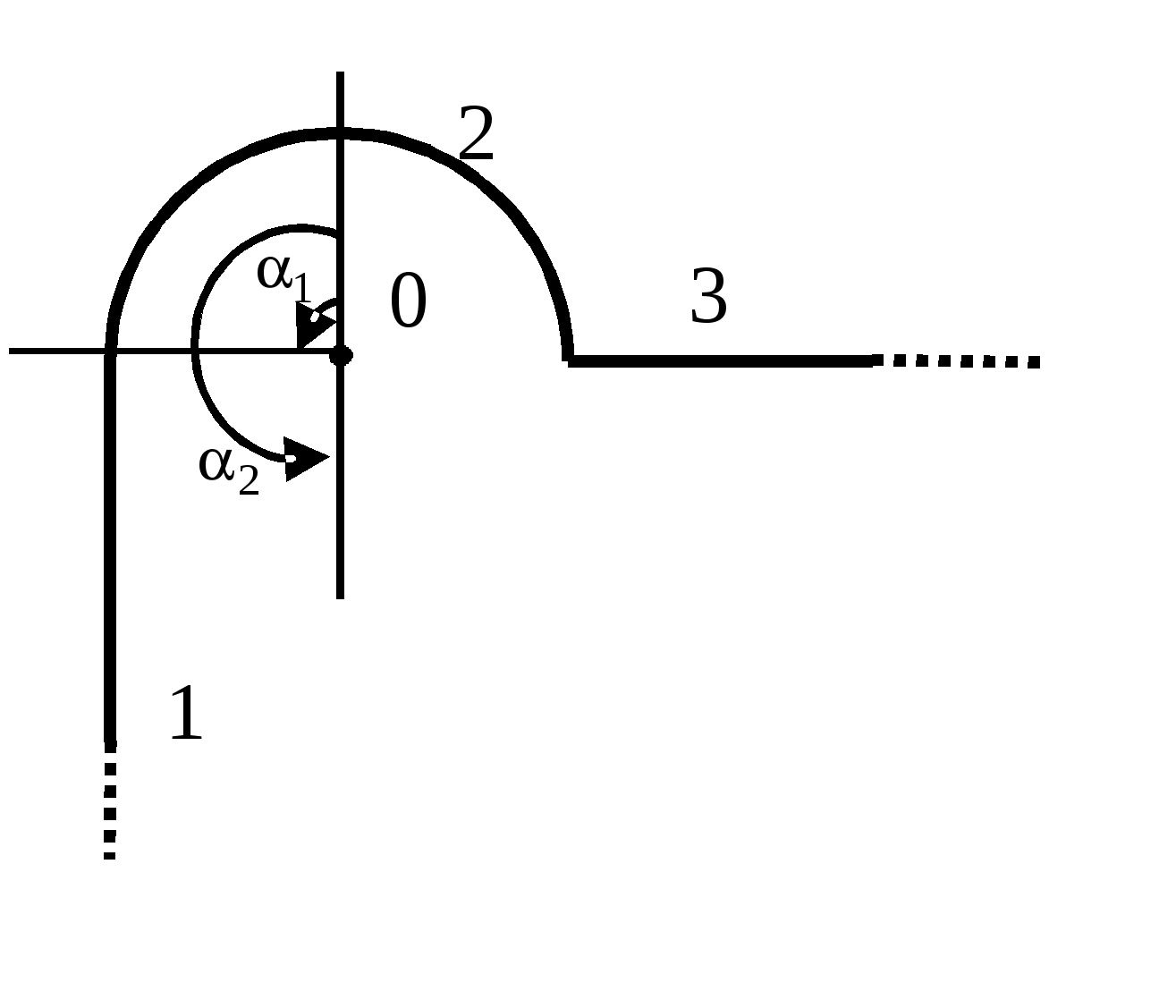

Однородно заряженная нить, на единицу длины которой приходится положительный заряд , имеет два полубесконечных прямолинейных и закругленный участки. Найдите модуль напряженности электрического поля в точке 0 для конфигурации, показанной на рисунке.

Решение. Нить, показанная на рисунке, имеет три участка - два прямолинейных полубесконечных (на рисунке участки 1 и 3) и один закругленный (на рисунке участок 2). Для решения задачи воспользуемся принципом суперпозиции полей, создаваемых каждым из трех участков нити в точке 0.

Выберем оси координат так, чтобы начало координат совпадало с точкой 0, а оси x и у совпадали с полубесконечными участками 1 и 3 (рис.).

Напряженность поля полубесконечной нити в точке, лежащей на перпендикуляре к оси нити (участок 1) будет иметь составляющие вдоль осей xи у, которые согласно результату примера 1.13, проекции которых равны

,

а направления показаны на рисунке.

Согласно результату примеру 1.4, напряженность поля полукольца (участок 2) в точке 0 будет направлена вдоль оси у иравна

(рис.).

Согласно результату задачи 1.13, результирующая напряженность поля полубесконечной нити в точке 0, лежащей на оси нити (участок 3) будет направлена вдоль оси xиравна

(рис.).
Сложив попарно проекции векторов, направленные вдоль осей xи у:

,

,

Найдем величину напряженности в точке 0:

,

то есть модуль вектора напряженности электрического поля в точке 0 равен , а направление вектора противоположно направлению оси у .