Задание по начертательной геметрии. Задача 2 (эпюр 1). Закон образования каркаса гиперболического параболоида (косой плоскости) l m l m l Г

• Название: Закон образования каркаса гиперболического параболоида (косой плоскости) l m l m l Г
• Анкор: Задание по начертательной геметрии
• Дата: 09.10.2021
• Размер: 103.57 Kb.
• Имя файла: Задача 2 (эпюр 1).docx
• Тип: Закон; #244240

Задача: Построить проекции гиперболического параболоида (косой плоскости) (n,m,Г), в(в₂) , в =?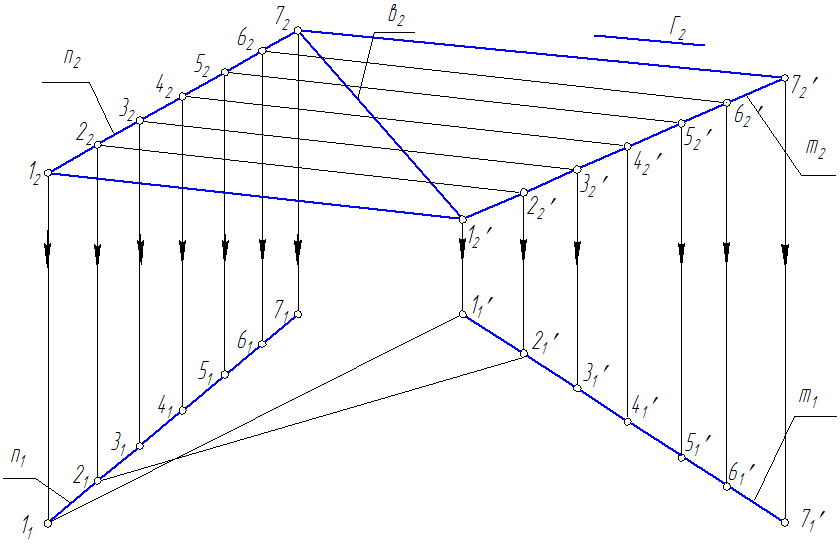



Закон образования каркаса гиперболического параболоида (косой плоскости) lm; lm; l Г

1. На П₂ разделим фронтальную проекцию направляющей n₂ на 7 точек.

2. Проведем через каждую точку проекцию образующей параллельно Г₂ – плоскости параллелизма.

3. На П₁ построим проекции точек и проведем проекции образующих через одноименные точки.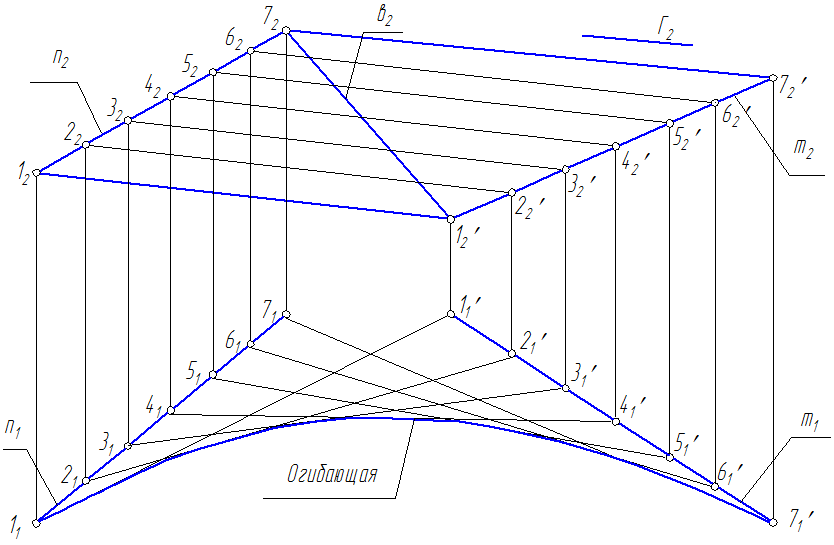



4. На П₁ определяем видимость поверхности: образующая 77’ - выше всех, она видна вся; образующая 66’ не видна только в одной точке, за 7 образующей; образующая 55’ не видна между 66’ и 77’; образующая 44’ не видна между 55’, 66’ и 77’; образующая 33’ не видна между 44’, 55’, 66’ и 77’; образующая 22’ не видна между 33’, 44’, 55’, 66’ и 77’; образующая 11’ не видна за всеми (от 2 до 7). Крайние проекции образующих (с учетом видимости) обвести основной линией.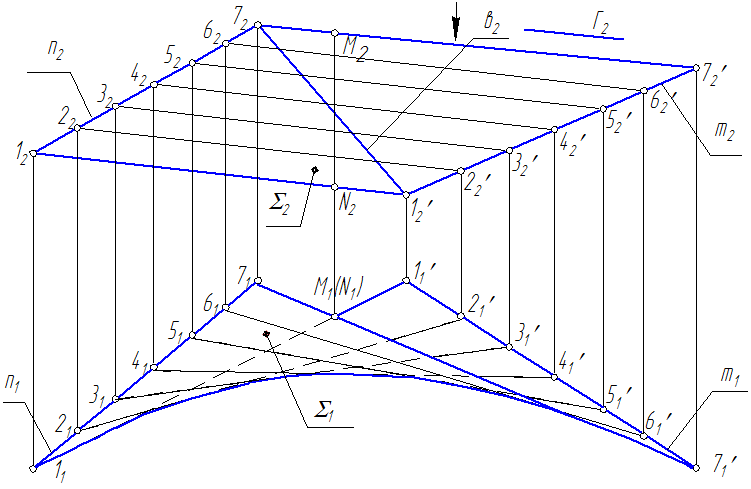



MN – горизонтально конкурирующие точки

5. Для построения горизонтальной проекции линии в(в₁) отметим звездочками точки пересечения в(в₂) с фронтальными проекциями образующих поверхности. Проведем линии связи из этих точек на соответствующие горизонтальные проекции образующих.

6. С учетом видимости соединим точки (звездочки) и получаем горизонтальную проекцию кривой в(в₁).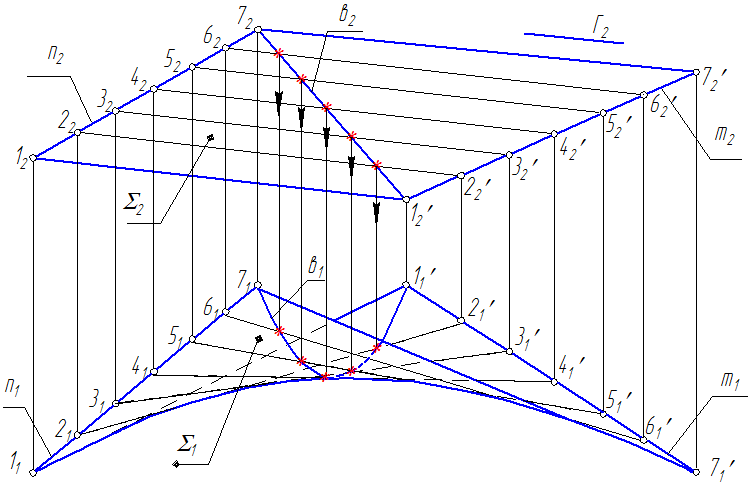