2.18. Прозрачный кубик лежит на монете. Монета освещается рассеянным светом.. обмен. Закон преломления на боковой грани кубика имеет вид
 Скачать 58.9 Kb. Скачать 58.9 Kb.
|
|
ЗАДАЧА №2.18 Прозрачный кубик лежит на монете. Монета освещается рассеянным светом. Определите, при каком значении показателя преломления материала кубика монета не будет видна через его боковую поверхность.  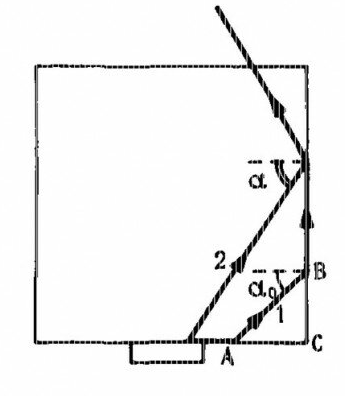 Для того, чтобы через боковую поверхность не была видна монета, необходимо, чтобы лучи или отражались от боковой поверхности кубика или в крайнем случае скользили вдоль нее. Из этого следует, что луч должен падать на боковую поверхность под углом, большим или равным предельному углу: 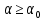 . Из рисунка очевидно (∆ABC), что самый маленький угол падения на боковую грань будет у луча, преломленного у основания под предельным углом, и, следовательно, наибольшая вероятность выхода через боковую грань у лучей, падающих на основание под углом, близким к π/2. Таким образом, если луч, дважды преломившись, будет скользить вдоль боковой поверхности кубика, то все остальные лучи, имеющие меньший угол падения, будут падать на боковую поверхность под углом, большим . Из рисунка очевидно (∆ABC), что самый маленький угол падения на боковую грань будет у луча, преломленного у основания под предельным углом, и, следовательно, наибольшая вероятность выхода через боковую грань у лучей, падающих на основание под углом, близким к π/2. Таким образом, если луч, дважды преломившись, будет скользить вдоль боковой поверхности кубика, то все остальные лучи, имеющие меньший угол падения, будут падать на боковую поверхность под углом, большим 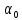 , и отразятся от нее: , и отразятся от нее: 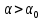 .(например, луч 2). Для первого преломления луча, отраженного от монеты, на основании кубика справедливо выражение: .(например, луч 2). Для первого преломления луча, отраженного от монеты, на основании кубика справедливо выражение:sinX/2/β=n Закон преломления на боковой грани кубика имеет вид: 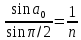 откуда, а так как треугольник ABC – прямоугольный, угол между нормалью к основанию и нормалью к боковой поверхности равен π/2, 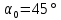 . Откуда . Откуда 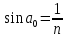 и и 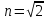 . . |
