Закон распределения случайной величины одно из фундаментальных понятий теории вероятностей
 Скачать 43.09 Kb.
|
|
Существует мнение, что «Математика – царица наук». Возможно, так и есть. Но для нас с Вами математика – это великолепный инструмент, который позволяет планировать и прогнозировать эксперимент. Целью сегодняшней нашей встречи является изучение статистических методов оценки погрешности химического анализа (т.е. как ответить на вопрос оппонента – насколько достоверны Ваши результаты? а какая точность анализа? и т.д.). Сначала давайте введем и дадим определения понятиям, которыми мы будем пользоваться. Слайд 2. Что же такое математическая статистика и чем она занимается? Точно так же, как химики работают с химическими веществами, математическая статистика оперирует случайными величинами. Слайд 3. Рассмотреть пример непрерывной случайной величины с pH воды: деионизированная/бидистилят, дистиллированная, талая, питьевая и т.д.. Слайд 4. Случайными величинами являются не только отдельные результаты измерений xi, но и их средние 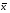 и все производные от них величины. 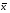Поэтому может служить лишь приближенной оценкой результата измерения. К нашему счастью можно оценить диапазон значений, в котором с заданной вероятностью P может находиться результат. Дадим определение понятию вероятность: … Эта вероятность P называется доверительной вероятностью, а соответствующий ей интервал значений – доверительным интервалом. Уровень значимости, выраженный в процентах, показывает, сколько раз в каждых ста испытаниях мы рискуем ошибиться, принимая случайное событие за значимое. Слайд 5. слайд Закон распределения случайной величины – одно из фундаментальных понятий теории вероятностей. слайд. Информация об общем виде функции распределения необходима поскольку, даже если истинные значения и вероятности (вероятность – площадь заштрихованной области на рисунке) совпадают, то для разных распределений интервал будет разным: Рассмотрим функцию распределения, приведенную на рис. 1. По оси абсцисс откладываются все возможные значения неприрывной случайной величины x, а по оси ординат – вероятности их появления. Как Вы думаете, какое значение случайной величины x наиболее часто встречаются? В качестве примера не случайно приведена колоколообразная, симметричная функция распределения. Именно такой ее вид наиболее характерен для результатов химического анализа и называется функцией нормального (или гауссова) распределения: Параметры этой функции m и s характеризуют: m – положение максимума кривой, т.е. собственно значение результата анализа, а s – ширину «колокола», т.е. воспроизводимость результатов. На практике химику приходится работать с ограниченной серией измерений. Выборка – … Можно показать, что среднее 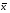является приближенным значением m, а стандартное отклонение s(x) – приближенным значением s. Естественно, эти приближения тем точнее, чем больше объем экспериментальных данных, из которых они рассчитаны, т.е. чем больше число параллельных измерений n и, соответственно, число степеней свободы f.Слайд 6. Теперь давайте немножко отвлечемся и обратимся к ПСХЭ им. Дмитрия Ивановича Менделеева. Как Вы знаете, одной из важнейших характеристик атома является его массовое число. В периодической таблице оно приведено … И тут у меня к Вам возникает вопрос: почему массовые числа химических элементов в ПСХЭ не являются целочисленными значениями (а ведь относительные массы протона и нейтрона равны 1)? Беседа, в результате которой выясняются три причины: изотопы, дефект массы и погрешность измерений. Слайд 8. Получается, что любой измерительный процесс подвержен действию множества факторов, искажающих результаты измерения. Отличие результата измерения от истинного значения измеряемой величины называется погрешностью. Ввиду того, что любой результат измерения содержит погрешность, точное значение измеряемой величины никогда не может быть установлено. Но, как мы с Вами уже отмечали, можно указать некоторый диапазон значений, в пределах которого может, с той или иной степенью достоверности, находиться истинное значение. В суммарную неопределенность результата измерения вносят вклад погрешности, которые можно разделить на два типа. Пусть в результате однократного измерения некоторой величины получено значение x*, отличающееся от истинного значения x0. Повторим измерение еще несколько раз. Возможные варианты взаимного расположения серии измеренных значений и истинного значения показаны на рис. В первом случае наблюдается разброс данных относительно среднего значения из результатов измерения. Такая составляющая неопределенности называется случайной погрешностью. Во втором случае имеет место смещение всей серии данных (и ее среднего) относительно истинного значения. Соответствующая составляющая неопределенности называется систематической погрешностью. Разумеется, в реальном случае мы всегда имеем и систематическую, и случайную составляющую. Так, на нижнем рис наряду со значительным смещением данных мы видим и некоторый их разброс, а на верхнем – на фоне большого разброса незначительное смещение среднего относительно истинного. Происхождение систематических и случайных погрешностей связано с различной природой факторов, воздействующих на измерительный процесс. Факторы постоянного характера или мало изменяющиеся от измерения к измерению вызывают систематические погрешности, быстро изменяющиеся факторы – случайные погрешности. С понятиями систематической и случайной погрешностей тесно связаны два важнейших метрологических понятия – правильность и воспроизводимость. слайд Случайную составляющую погрешности предложено характеризовать с помощью воспроизводимости. слайд Обобщающее понятие, характеризующее малость любой составляющей неопределенности – как систематической, так и случайной, – называется точностью. Рассмотрим основные способы количественной оценки воспроизводимости результатов химического анализа. Слайд 9. Поскольку воспроизводимость характеризует степень рассеяния данных относительно среднего значения, для оценки воспроизводимости необходимо предварительно вычислить среднее 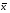из серии результатов повторных (параллельных) измерений x1, x2, ... xn:Отметим, что в обрабатываемой серии должны отсутствовать промахи – отдельные значения, резко отличающиеся от остальных и, как правило, полученные в условиях грубого нарушения измерительной процедуры (аналитической методики). Поэтому прежде всего (еще до вычисления среднего) следует с помощью специальных статистических тестов, которые мы рассмотрим позднее, проверить серию данных на наличие промахов и, при обнаружении таковых, исключить их из рассмотрения. В качестве меры разброса данных относительно среднего чаще всего используют выборочную дисперсию и производные от нее величины – (абсолютное) стандартное отклонение и относительное стандартное отклонение По смыслу дисперсия есть усредненная величина квадрата отклонения результата измерения от своего среднего значения. Несмотря на то, что числитель выражения содержит n слагаемых, знаменатель равен n–1. Причина состоит в том, что среди n слагаемых числителя только n–1 независимых (поскольку по n–1 значениям xi и среднему 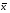всегда возможно вычислить недостающее n–е слагаемое). Величина знаменателя в выражении обозначается f и называется числом степеней свободы дисперсии s2(x). В химическом анализе для характеристики воспроизводимости обычно используют не дисперсию, а абсолютное или относительное стандартное отклонение. Это объясняется соображениями практического удобства. Размерности s(x) и x совпадают, поэтому абсолютное стандартное отклонение можно непосредственно сопоставлять с результатом анализа. Величина же sr(x) – безразмерная и потому наиболее наглядная. С помощью относительных стандартных отклонений можно сравнивать между собой воспроизводимости не только конкретных данных, но и различных методик и даже методов в целом. Среди всех существующих методов химического анализа наилучшие воспроизводимости (т.е. наименьшие sr) характерны прежде всего для «классических» химических методов анализа – титриметрии и, особенно, гравиметрии. В оптимальных условиях типичные величины sr для них составляют порядка n.10–3 (десятые доли процента). Среди инструментальных методов такой же (а в ряде методик – и более высокой) воспроизводимостью обладает кулонометрия, особенно в прямом варианте (до n.10–4). Большинство прочих инструментальных методов характеризуются величинами sr от 0.005 до 0.10. Методы с еще более низкой воспроизводимостью относятся к полуколичественным. Они часто отличаются исключительной простотой, экспрессностью, экономичностью (тест-методы) и очень полезны, например, для быстрой оценки состояния окружающей среды. Слайд 10. Еще раз отметим, что ввиду наличия случайной погрешности одна и та же величина x при каждом последующем измерении приобретает новое, непрогнозируемое значение, т.е. является случайной величиной. При обработке результатов химического анализа распространенной является ситуация, когда случайная величина имеет заведомо нормальное или близкое к нормальному распределение, но представляющая ее выборочная совокупность маленькая (2 слайд Численные значения коэффициентов пропорциональности t называются коэффициентами Стьюдента. Коэффициенты Стьюдента для различных значений P и f приведены в табл. 1 (приложение). Если мы внимательно посмотрим на данные таблицы, то заметим следующие закономерности … слайд При расчете доверительного интервала встает вопрос о выборе доверительной вероятности P. При слишком малых значениях P выводы становятся недостаточно надежными. Слишком большие (близкие к 1) значения брать тоже нецелесообразно, так как в этом случае доверительные интервалы оказываются слишком широкими, малоинформативными. Для большинства химико-аналитических задач оптимальным значением P является 0.95. Именно эту величину доверительной вероятности (за исключением специально оговоренных случаев) мы и будем использовать в дальнейшем. Слайд 11. 1) Q-критерии. Тестовая статистика Q-критерия вычисляется по формуле:  Эта формула верна для числа измерений m=3..7. При m=8..10 в знаменателе должна стоять разница между подозрительным значением и ближайшем к максимальному (или минимальному). Значение Q сравнивают с табличным значением, и если табличное значение критерия меньше тестовой статистики, то подозрительный результат является промахом и исключается из дальнейшего рассмотрения. При этом обычно доверительную вероятность берут равной 0.90, а не 0.95. В данном случае это является некоторым "ужесточением" требований: лучше выбросить значение, не являющееся промахом (т.е. допустить ошибку первого рода), чем оставить промах в выборке. Как правило, на промах проверяют минимальное и максимальное значение выборки. Q-критерий работает для выборок, содержащих 3-10 значений, при больших объемах выборки он становится нечувствителен к промахам.2) Критерий Стьюдента. Минимальное и максимальное значения xкр являются грубыми промахами, если параметр τ, рассчитанный как 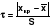 , превышает табличный τкр для принятой доверительной вероятности и числе степеней свободы f=m-1. Критерий Стьюдента является более универсальным, поскольку позволяет учесть разброс данных внутри выборки относительно друг друга.Алгоритм сравнения 2-х независимых выборок Задача сравнения результатов химического анализа состоит в том, чтобы выяснить, является ли различие между ними значимым или такие выборки можно считать принадлежащими одной генеральной совокупности.
|
, где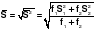 
. Критическим значением служит коэффициент Стьюдента для выбранной доверительной вероятности и числе степеней свободы f= f1+f2=n1+n2-2.