[7 семестр] Расписанные вопросы к экзамену. Закономерностей. 4 Понятия информационный объект, информационное взаимодействие
 Скачать 0.84 Mb. Скачать 0.84 Mb.
|
30. Линейная модель механизма поиска по логическому выражению.Логическое выражение поискового условия – это синтаксическая конструкция языка, задающая порядок и способ вычисления величины, принимающей значение «0» или «1». Выражение представляет собой последовательность операндов, соединенных друг с другом знаками операций. Нотация Бэкуса для такого выражения следующая: <Выражение>::=<Операнд><Выражение><Операция> <Выражение> (<Выражение><Операция><Выражение>) Обычно: операнд – термин(дескриптор); операция – одна из логических операций. Первый этап вычисления логического выражения может состоять в построении двоичного дерева операций. Все логические операции (кроме NOT) – бинарные => можно представить любое логическое выражение запроса в виде несбалансированного двоичного дерева, прохождение по которому снизу вверх приводит к получению результата. В узлах дерева расположены логические операции (oi), а листья (конечные узлы) представляют собой строки матрицы L0, соотвующие терминам запроса 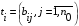 .Операнд запроса – отдельно вычисляемое выражение, соответствующее поддереву запроса. Расширенная матрица «термин-документ» .Операнд запроса – отдельно вычисляемое выражение, соответствующее поддереву запроса. Расширенная матрица «термин-документ» 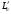 . Строки – не только показатели встречаемости терминов, но и результирующие векторы запросов (Qi). . Строки – не только показатели встречаемости терминов, но и результирующие векторы запросов (Qi).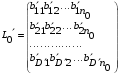 , где 1,K – количество включенных в матрицу результирующих векторов запросов,а , где 1,K – количество включенных в матрицу результирующих векторов запросов,а  Поставим в соответствие каждой логической операции правило ее выполнения с использованием расширенной матрицы: 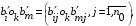 где где 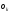 из множества бинарных логических операций: из множества бинарных логических операций: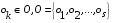 Для унарной операции NOT это правило реализуется следующим образом: Для унарной операции NOT это правило реализуется следующим образом: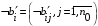 Тогда алгоритм разрешения двоичного дерева поискового запроса состоит в последовательном выполнении снизу вверх логических операций и в пополнении на каждом шаге матрицы L0 очередной строкой-результатом. Условием выполнения k-той операции служит наличие в матрице 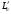 строк, соответствующих правому и левому операнду. После выполнения k-той операции формируется результирующий вектор строк, соответствующих правому и левому операнду. После выполнения k-той операции формируется результирующий вектор 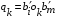 , который становится ( , который становится (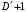 )-й строкой матрицы. )-й строкой матрицы.31. Линейная модель механизма поиска документов-аналогов.Аналогами документа называются такие документы информационного массива, которые имеют заданное количество общих терминов с исходным. Задается пороговое значение близости m. Процедура поиска аналогов м.б. усложнена заданием пороговых значений для структурных единиц документов и составлением логических выражений над множеством критериев отбора, связывающих поле и соответствующее пороговое значение.Выделим в матрице L0 столбец 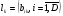 , соответствующий ПОДу рассматриваемого документа, и построим подматрицу LDoc, оставив в матрице L0 те строки, в кот-х , соответствующий ПОДу рассматриваемого документа, и построим подматрицу LDoc, оставив в матрице L0 те строки, в кот-х 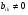 . По матрице LDoc строится результирующий вектор запроса на поиск аналогов (QDoc ) и м.б. получен поисковый результат с учетом (или без) некоторого заданного порога «близости» (m). Результирующий вектор QDoc=(q1q2…qm), где qi= . По матрице LDoc строится результирующий вектор запроса на поиск аналогов (QDoc ) и м.б. получен поисковый результат с учетом (или без) некоторого заданного порога «близости» (m). Результирующий вектор QDoc=(q1q2…qm), где qi=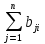 , т.е. суммированием элементов столбца. Далее получаем окончательный поисковый результат Kn=(k1…km), ki равно либо 0 (qi , т.е. суммированием элементов столбца. Далее получаем окончательный поисковый результат Kn=(k1…km), ki равно либо 0 (qi32. Линейная модель механизма эвристического поиска.Пользователь изначально указал некоторое множество релевантных документов. Шаг 1. Построение словника терминов по множеству релевантных документов. Т.е. строится матрица LRel. Шаг 2. Оценка терминов словника и построение Поискового Образа Темы (ПОТ). Результатом оценивания должно быть выделение тех терминов, которые могут быть включены в ПОТ. Рекомендованный способ отбора терминов: точность термина (=частота термина в множестве релевантных документов/частота термина в информационном массиве) должна превышать параметр, вычисляемый как 1/nS. Эвристический параметр nSхарактеризует число ожидаемых документов. Шаг 3. Построение матрицы «термин-документ» (получается вычеркиванием строк терминов, которые не попали в ПОТ). 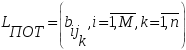 , где M – количество терминов в ПОТ, определяющее порог «близости» для следующего шага, n – число релевантных документов. //Столбец-термин, строка-документ , где M – количество терминов в ПОТ, определяющее порог «близости» для следующего шага, n – число релевантных документов. //Столбец-термин, строка-документШаг 4. Поиск аналогов с пороговым значением M. По матрице «термин-документ» формируется поисковый результат с учетом порога близости M. Если число документов полученного результата меньше, чем заданное в системе nS, то пороговое значение Mуменьшается на 1, и повторяется процедура поиска аналогов с новым пороговым значением. Таким образом, на каждой i-ой итерации пороговое значение равно M–i. Цикл заканчивается: либо после выполнения очередной итерации число документов результата стало равно или превысило значение nS , либо пороговое значение стало равно 0. |
