Замечательные кривые оя. Замечательные кривые розы и спирали Цель работы
 Скачать 234.04 Kb. Скачать 234.04 Kb.
|
|
Замечательные кривые:розы и спирали Цель работы: Познакомить с некоторыми поистине замечательными кривыми, которые встречаются и имеют практическое применение в нашей жизни. Задачи проекта: Я считаю, что моя работа пригодится учителям доступно и красочно продемонстрировать учащимся практическое применение свойств замечательных кривых, научить строить кривые при помощи несложных школьных инструментов Объектом исследования: являются замечательные кривые розы и спирали Актуальность: в школьном курсе не достаточно рассматриваются свойства и применение таких замечательных кривых как розы и спирали Гипотеза: Кривая (линия) - след, оставленный движущейся точкой или телом. Обычно кривую представляют лишь как плавно изгибающуюся линию, вроде параболы или окружности. Но математическое понятие кривой охватывает и прямую, и фигуры, составленные из отрезков прямых, например, треугольник или квадрат.В школьном курсе математики в качестве кривых рассматриваются графики функций. Спираль архимеда Безобидная воронка, образованной вытекающей из ванны водой; свирепый смерч, опустошающий все на своем пути; величественный круговорот гигантского космического вихря туманностей и галактик – все они имеют форму спиралей. Одну из первых спиралей, описанную Архимедом, нам продемонстрирует светлячок. Отправим его в путешествие вдоль секундной стрелки часов, полагая, что он будет перемещаться с постоянной скоростью, не обращая внимания на равномерное движение стрелки часов по кругу. Если вообразить бесконечно, длинную стрелку, то жучок высветит нам «спираль Архимеда» (в переводе с латыни спираль означает «изгиб», «извив»). Геометрическим свойством, характеризующим спираль Архимеда, является постоянство расстояний между витками. Архимедова спираль – плоская кривая, описываемая точкой M, равномерно движущейся по прямой OA, в то время как эта прямая равномерно вращается в плоскости вокруг одной из своих точек O. Спираль Архимеда состоит из бесконечно многих витков. Она начинается в центре , и все более и более удаляется от него по мере того, как растет число оборотов. На рисунке изображены первый виток и часть второго 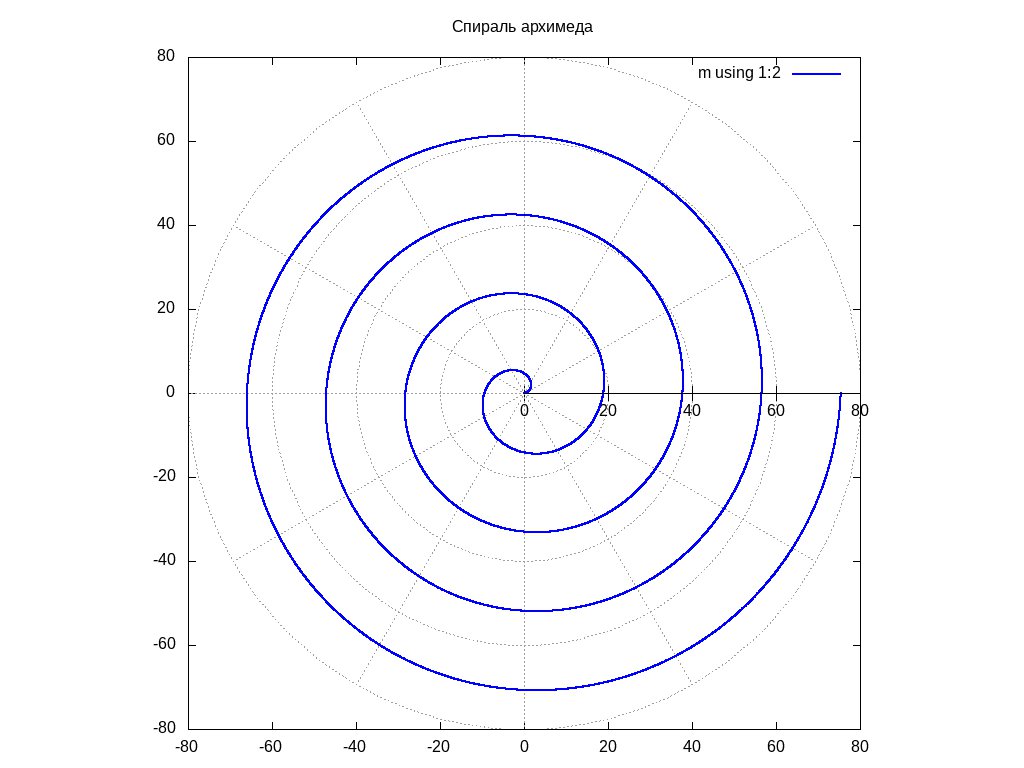 {\displaystyle \rho =a\sin k\varphi \,.}  роза гвиндо роза гвиндоРоза— плоская кривая, напоминающее символическое изображение цветка. первые об этой кривой упоминает флорентийский монах Гвидо Гранди в двух письмах Лейбницу в декабре 1713 года и называет её «розовидной». Через десять лет он опубликовал статью о ней в «Философских трудах Королевского общества», где рассмотрел разновидности этой кривой с различным количеством лепестков и также называл их «розовидными». Ещё через пять лет Гвидо Гранди развил теорию розовидных кривых в отдельном труде, где наряду с этим рассмотрел похожие на них пространственные кривые, лежащие на сфере, которые он назвал «клелиями» в честь княгини Клелии Борромео.  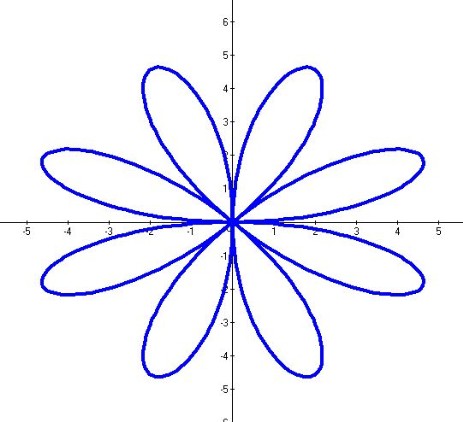 Полярная систем координат Понятие угла и радиуса были известны ещё в первом тысячелетии до н. э. Греческий астроном Гиппарх (190120 гг до н. э.) создал таблицу, в которой для разных углов приводились длины хорд. Существуют исвидетельства применения им полярных координат для определения положения небесных тел Архмед в своём сочинении «Спирали» описывает так называемую спираль Архимеда, функцию, радиус которой зависит от угла. Работы греческих исследователей, однако, не развились в целостное определение системы координат. Полярная система координат двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения триганаметрической уравнений. 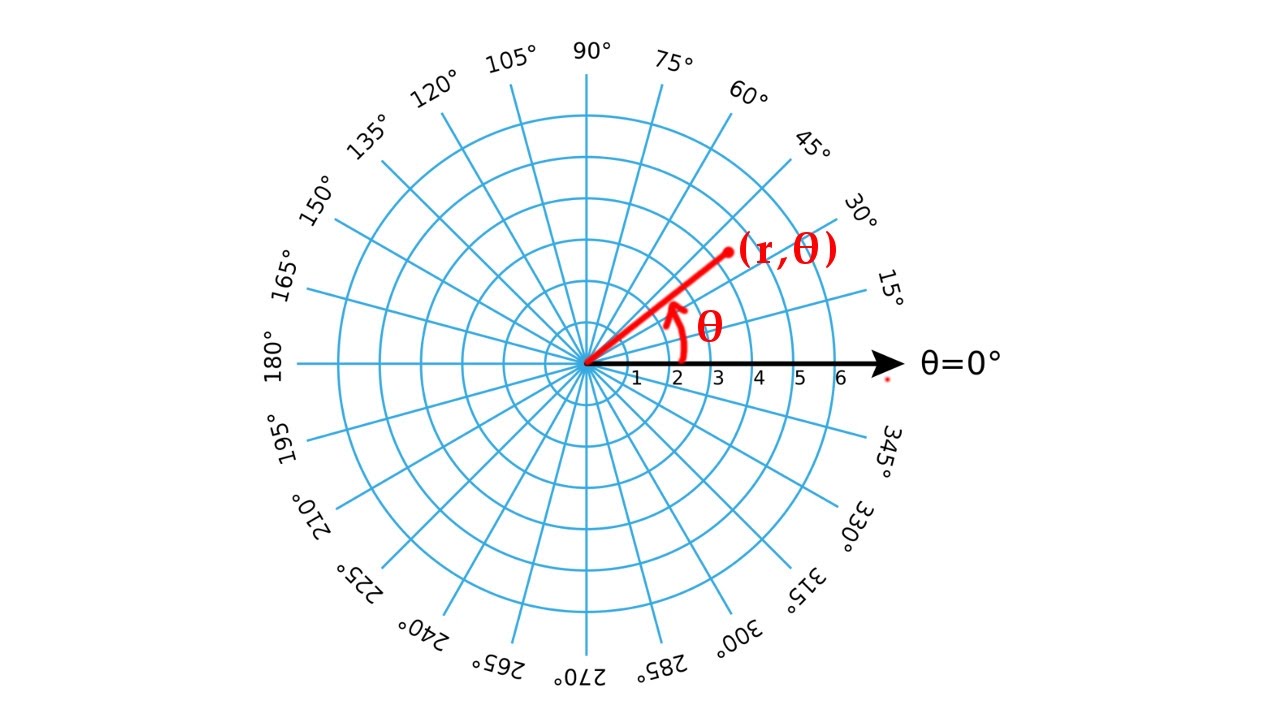 |
