Отчёт по лабораторым работам статистика. Отчёт по лабораторным работам 1 семестр. Занятие 1 Сводка и группировка данных статистического наблюдения
 Скачать 0.67 Mb.
|
|
Отчёт по лабораторным работам Лабораторное занятие 1 «Сводка и группировка данных статистического наблюдения» Цель работы: научиться вычислять данные структуры распределения, графически отображать структуру выборки с помощью диаграмм в программе Microsoft Excel. Ход выполнения работы: представлены данные о затратах на производство металлургического и машиностроительного заводов (млн. руб.).
Для решения задачи преобразуем исходную таблицу и выполним расчет относительных показателей структуры – частостей. Для этого выразим исходные данные в процентах к итогу:  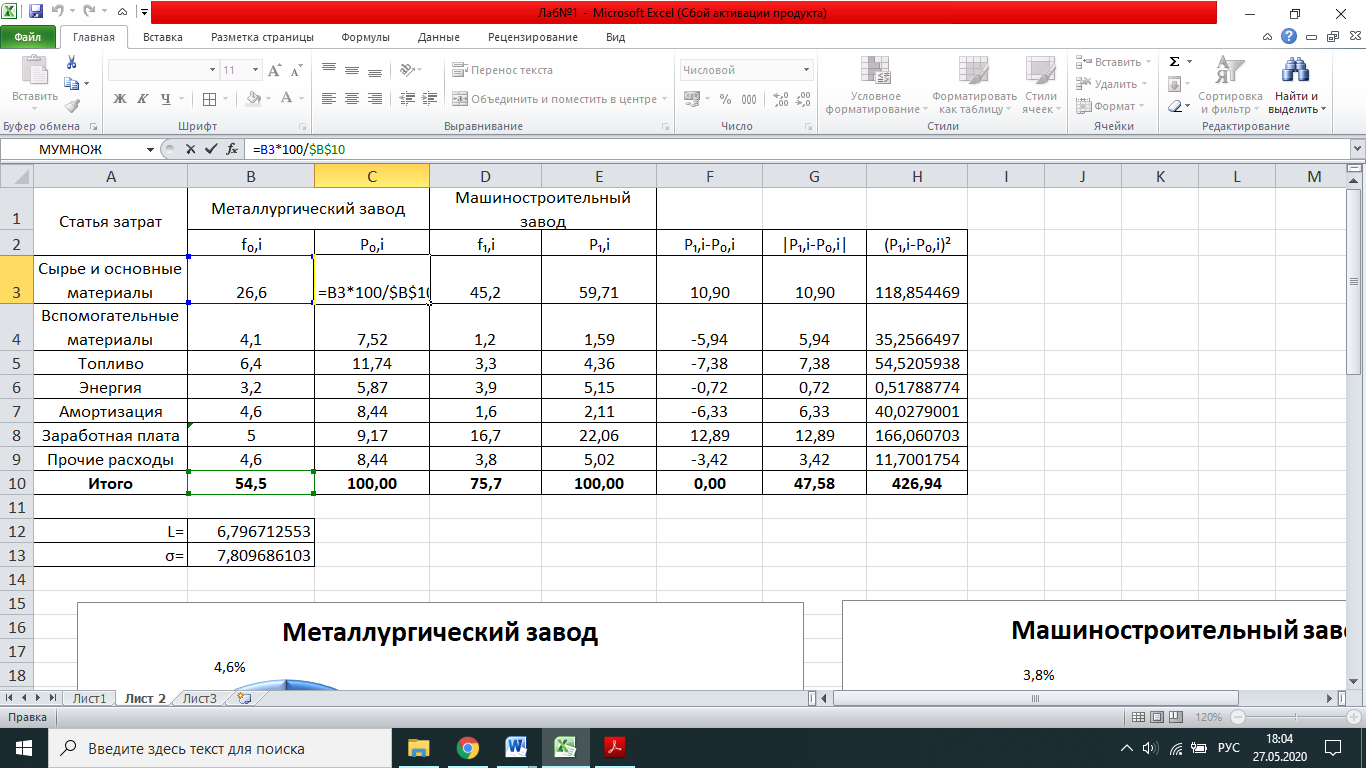 Рис. 1.1 Далее рассмотрим различие в показателях структуры. Для этого вычислим среднее линейное отклонение:  а также среднее квадратическое отклонение:  Расчеты в Microsoft Excel показаны на Рисунке 1.2. Полученные значения L и  показывают, на сколько процентов в среднем отличается удельный вес структурной группы.Рассмотрим построение круговой диаграммы с помощью Microsoft Excel. Для этого надо воспроизвести следующие действия: 1. На лист рабочей книги вывести данные таблицы в два столбика, выделить эти столбики с помощью мыши. (Если столбики находятся не рядом, то следует, выделив первый столбик, нажать и удерживать клавишу Ctrl во время выделения второго.) 2. Выбрать Вставка → Диаграммы → Круговая. 3. В диалоговом окне Круговая выбрать круговая или объемная круговая.  Рис. 1.2 4. При выборе Круговая появится диаграмма (рис. 1.3). На вкладке Конструктор есть возможность выбрать макет диаграммы.   Рис. 1.3 Для построения линейчатой диаграммы с помощью Microsoft Excel необходимо сделать следующее. После выбора столбцов данных выбрать Вставка → Диаграммы → Линейчатая. Макет диаграммы выбираем так же, как и в случае круговой диаграммы.  Рис. 1.4 Вывод: Таким образом, на основе полученных данных можно сделать вывод, что основной процент затрат составляют сырье и основные материалы (металлургический завод - 59,7%; машиностроителный - 48,8%). По металлургическому заводу % после сырья и основных материалов идёт заработная плата (22%), далее идёт энергия (5,1%), прочие расходы (5%) и топливо (4,3%), наименьший процент у амортизации (2,1%) и вспомогательных материалов (1,5%). У машиностроительного завода немного другая картина: наибольший процент после сырья идёт топливо (11,7%), далее заработная плата (9,1%). Одинаковы процент у прочих расходов и амортизации (8,4%) и самые наименьшие проценты у вспомогательных материалов (7,5%) и энергии (5,8%). Эти данные говорят о разных сферах деятельности и соответственно разных затратах. Лабораторное занятие 2 «Методы обработки и анализа статистической информации» Цель работы: научиться определять параметры вариации, используя Microsoft Excel. Ход выполнения работы: приведены данные по территории Поволжского федерального округа.
Введем исходные данные в программе Microsoft Excel. Ранжируем ряд по изучаемому показателю. Для этого выделим значения по субъектам в столбце численность фактически действующих индивидуальных предпринимателей всего 2017г. и нажмем кнопку «Сортировка по возрастанию», автоматически присоединяя данные в столбце с наименованиями (рис. 2.1).  Рис. 2.1 Найдем абсолютные параметры вариации: размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение; и относительные: коэффициент вариации, коэффициент осцилляции. Размах вариации – это разность между максимальным и минимальным значением:  Для определения остальных величин понадобится вычислить среднее x. Оно определяется по формуле простой средней. Для определения абсолютных параметров вариации добавим столбцы, вычисляющие промежуточные значения: 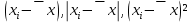 .Среднее линейное отклонение (СЛО): 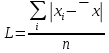 Дисперсия:  Среднее квадратичное отклонение (СКО):  Все вычисления приводим в отдельных ячейках под основной таблицей (рис. 2.2). СЛО и СКО определяют размеры вариации. В данном случае СЛО показывает, что индивидуальные значения численности фактически действующих индивидуальных предпринимателей всего 2017г. по субъектам ПФО отличаются от среднего в среднем на 12869,1 чел. СКО так же показывает средний размер отклонений показателя от средних значений и составляет в нашем случае 15666,4 чел. В соответствии со свойством мажоритарности средних СКО>СЛО. Для сравнительно оценки вариации необходимо определить коэффициенты осцилляции и вариации. Коэффициент осцилляции считается по формуле:  Коэффициент вариации: 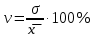 Значение коэффициента вариации превышает 33 %, следовательно, полученные результаты показывают, что средняя величина признака не отражает характерную величину признака и не является типичной, так как коэффициент вариации достаточно высок. 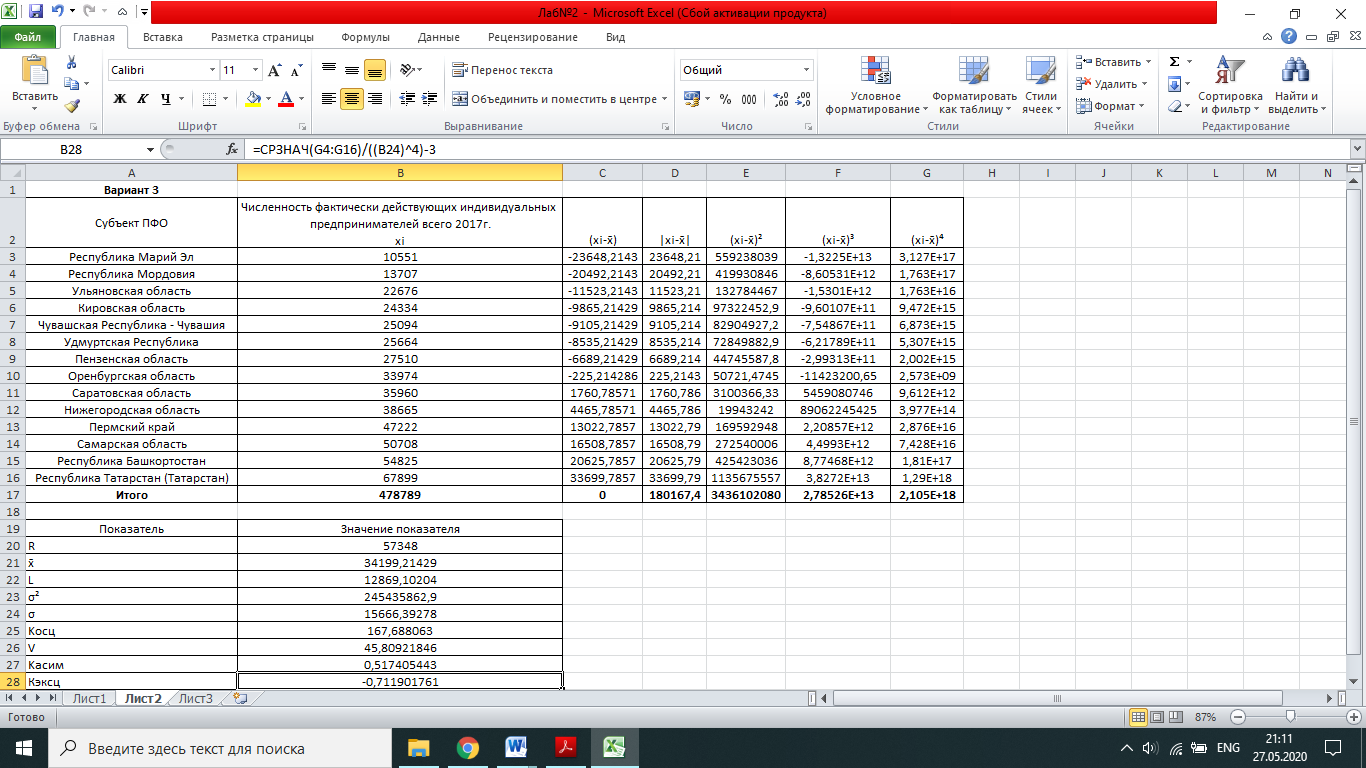 Рис.2.2 В нормальном распределении коэффициент асимметрии равен 0, а эксцесс равен трем. Коэффициент асимметрии определяет направление и меру сдвига фактического распределения по сравнению с нормальным и вычисляется по формуле: 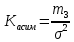 где  – центральный момент третьего порядка. Принято считать, что при коэффициенте асимметрии менее 1,5 – 1,7 выявленная асимметрия не является существенной. Коэффициент эксцесса оценивает крутизну распределения и вычисляется так: 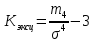 где 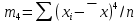 – центральный момент четвертого порядка. Отрицательное значение показателя отмечает более плоскую вершину фактического распределения по сравнению с нормальным. Вывод: На основании расчетов можно сделать вывод, что распределение субъектов ПФО по значениям численности фактически действующих индивидуальных предпринимателей в 2017г. достаточно однородно. Для этого распределения средняя величина признака не отражает характерную величину признака и не является типичной, так как коэффициент вариации достаточно высок. |