|
|
Занятие 14(Фдз 15). Занятие 14 (Фдз 15). Приведение квадратичной формы к каноническому виду ортогональным преобразованием координат|
Занятие 14 (Фдз 15).
Приведение квадратичной формы к каноническому виду ортогональным преобразованием координат.
14.1. Ортогональные преобразования координат. Приведение квадратичной формы к каноническому виду ортогональным преобразованием координат.
14.1. Ортогональным преобразованием координат называется преобразование координат векторов
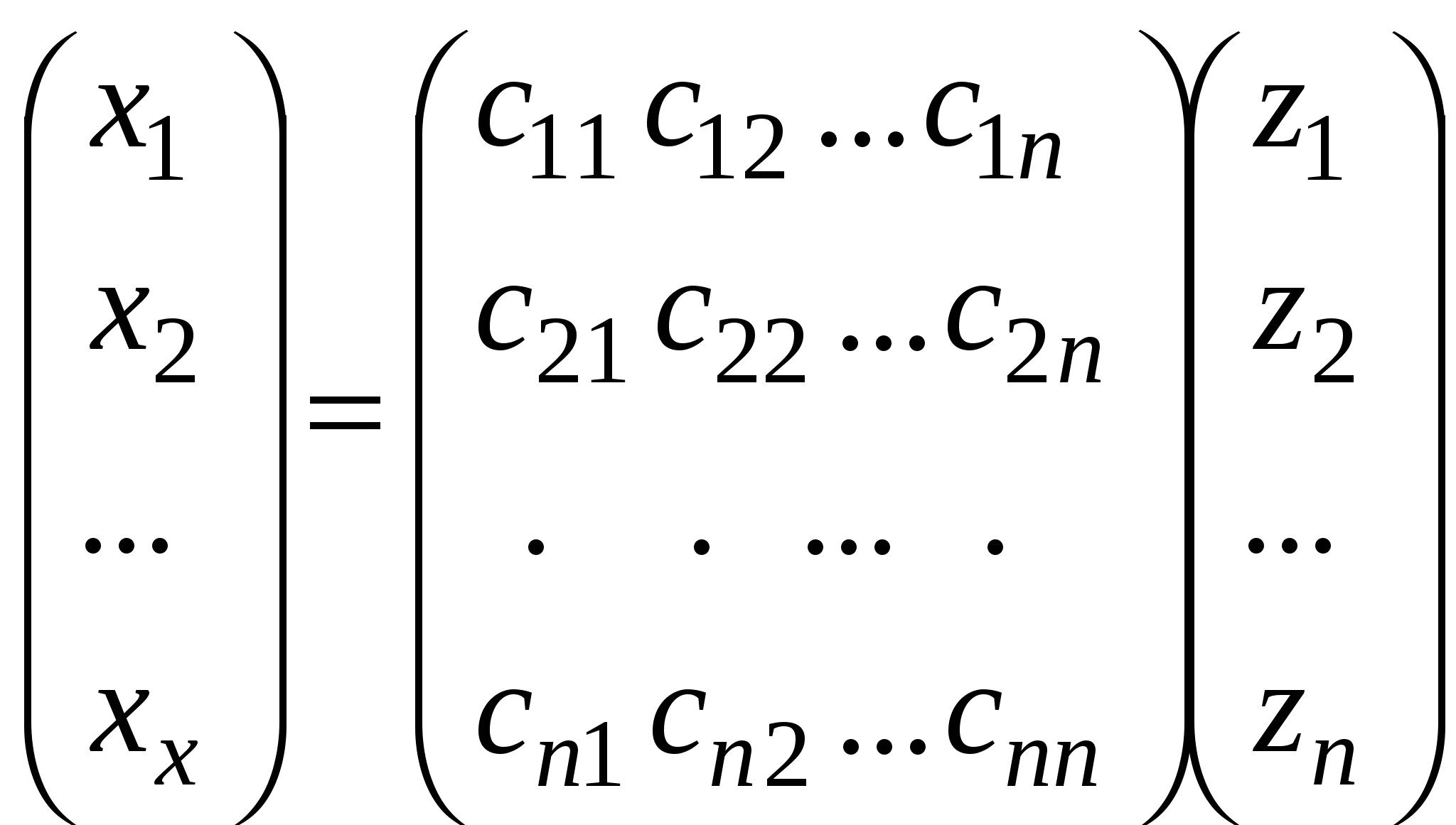 или или 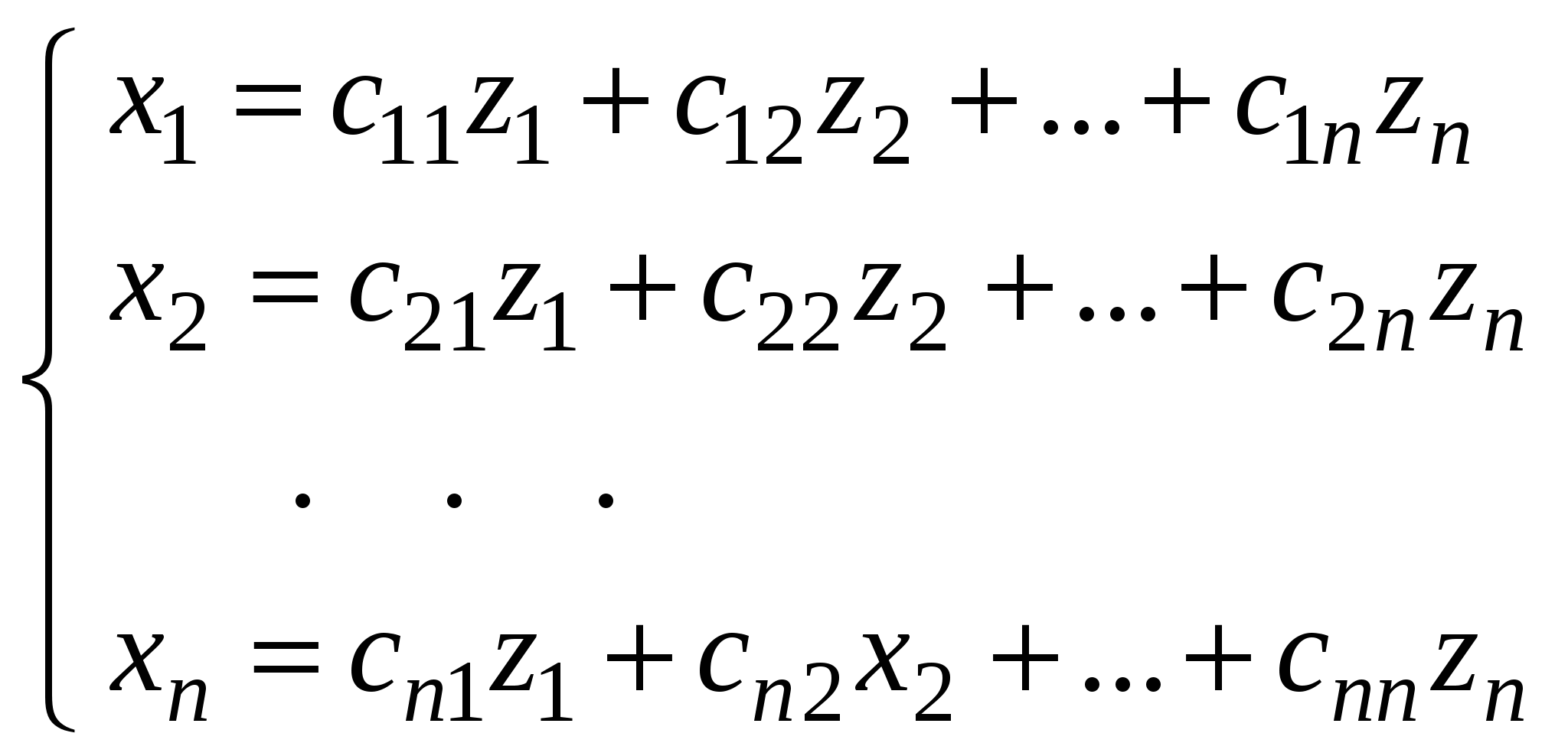 (1) (1)
при переходе от одного ортонормированного базиса 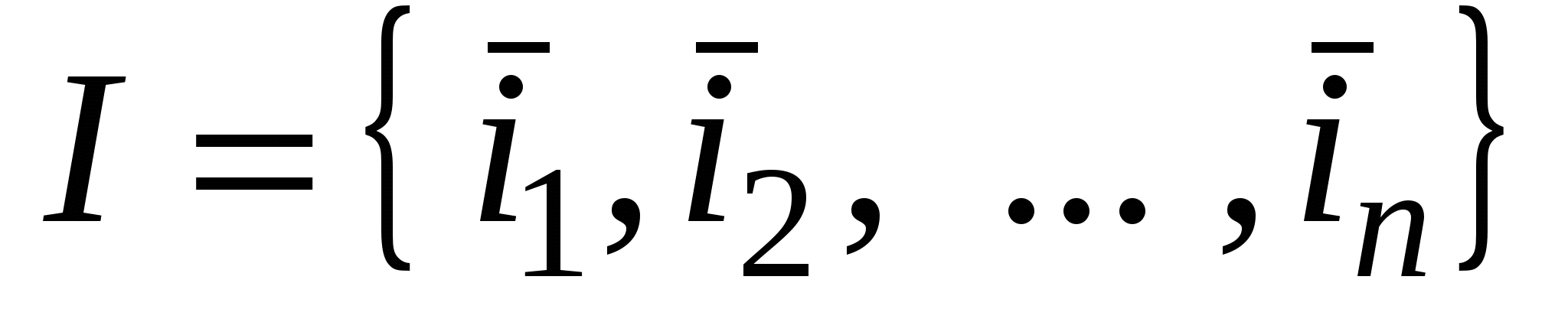 евклидова пространства евклидова пространства 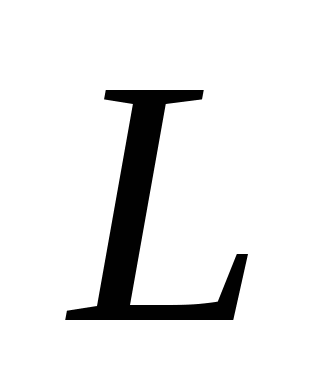 к другому ортонормированному базису к другому ортонормированному базису  этого пространства. Координаты этого пространства. Координаты 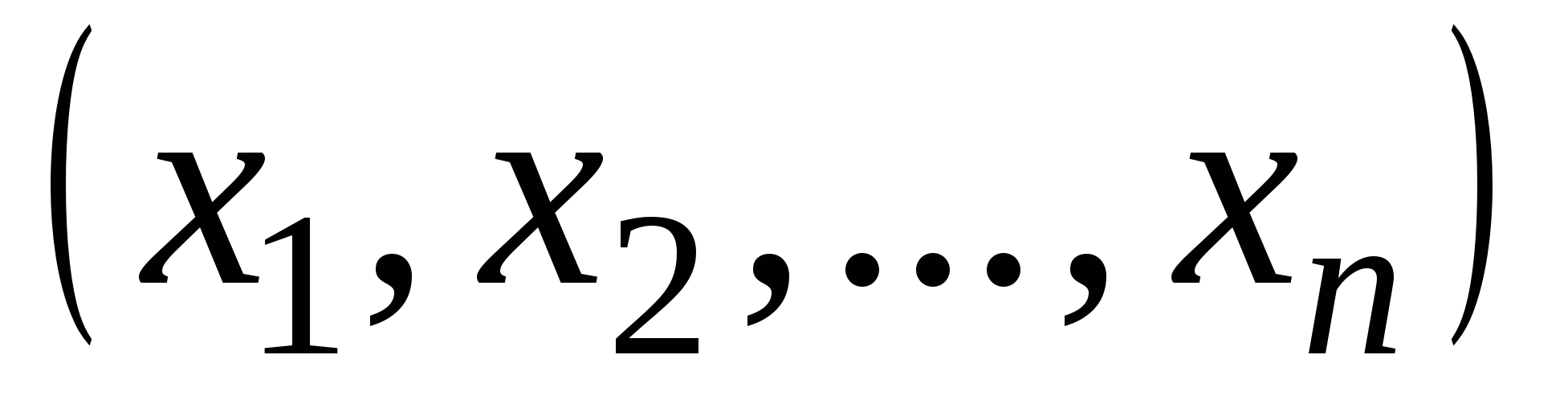 связаны с базисом связаны с базисом  , а координаты , а координаты  - с базисом - с базисом 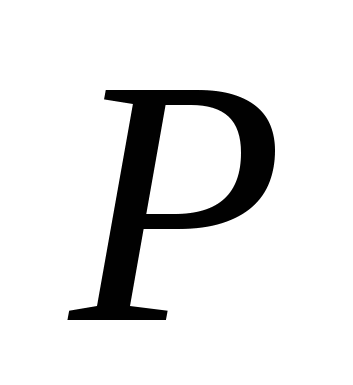 . .
Матрица 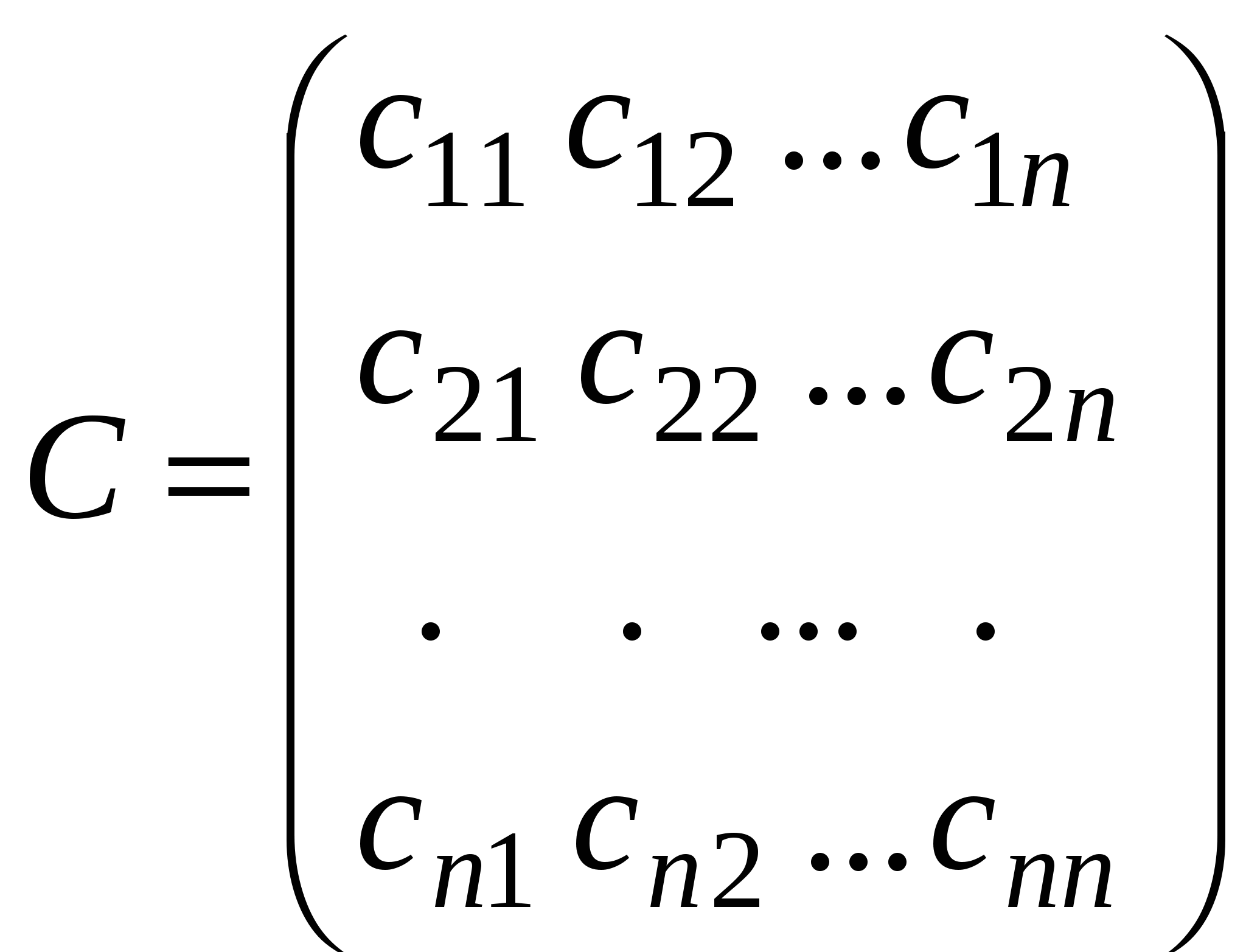 является ортогональной матрицей, т.е. является ортогональной матрицей, т.е. 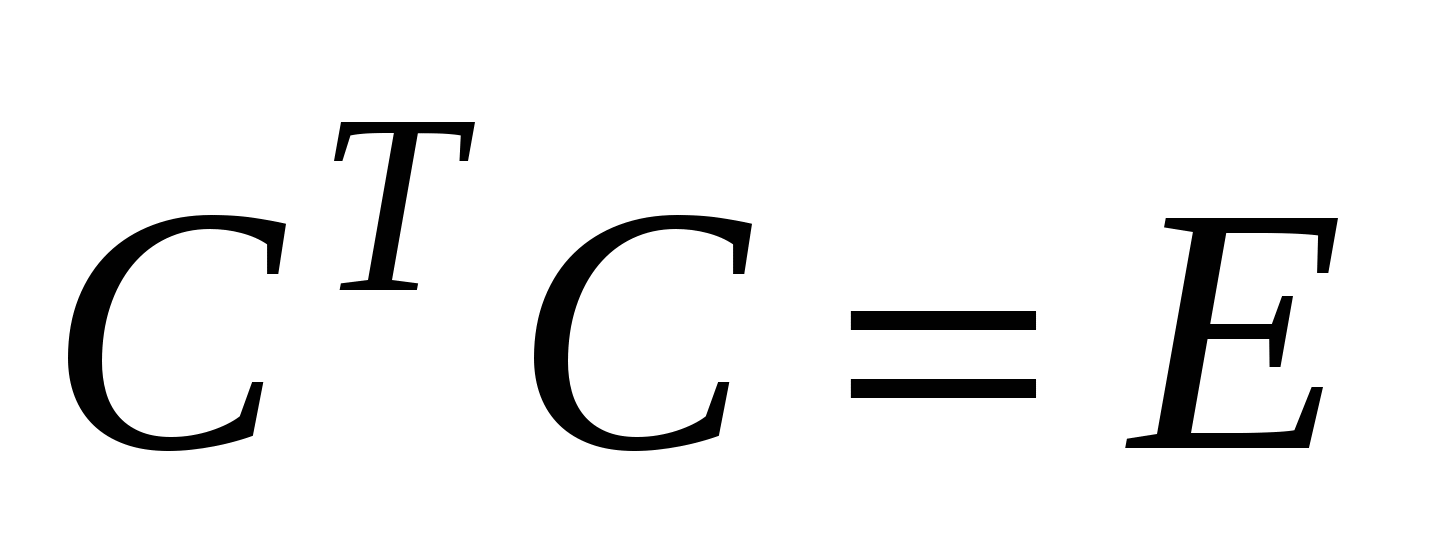 . .
Любую квадратичную форму 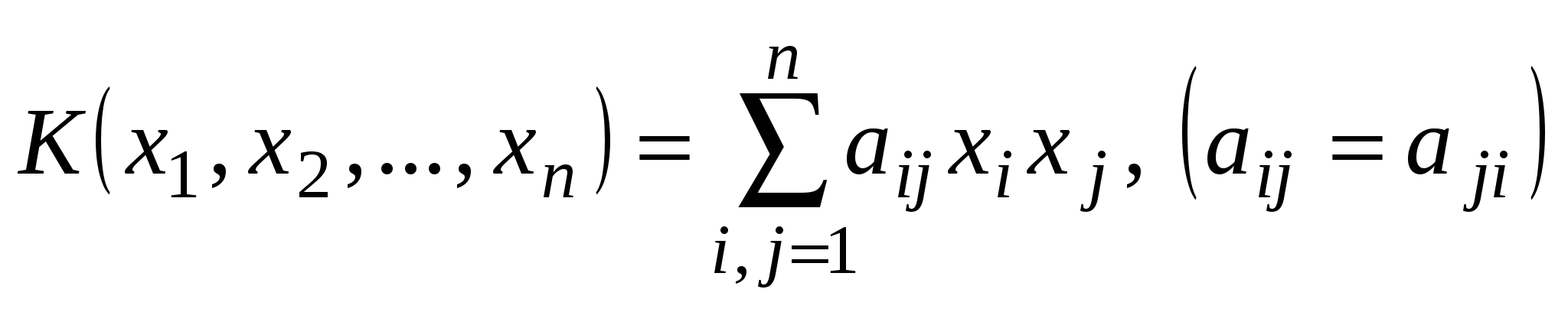 ортогональным преобразованием (1) координат можно привести к каноническому виду. Делается это последовательным выполнением следующих шагов. ортогональным преобразованием (1) координат можно привести к каноническому виду. Делается это последовательным выполнением следующих шагов.
Записывается матрица 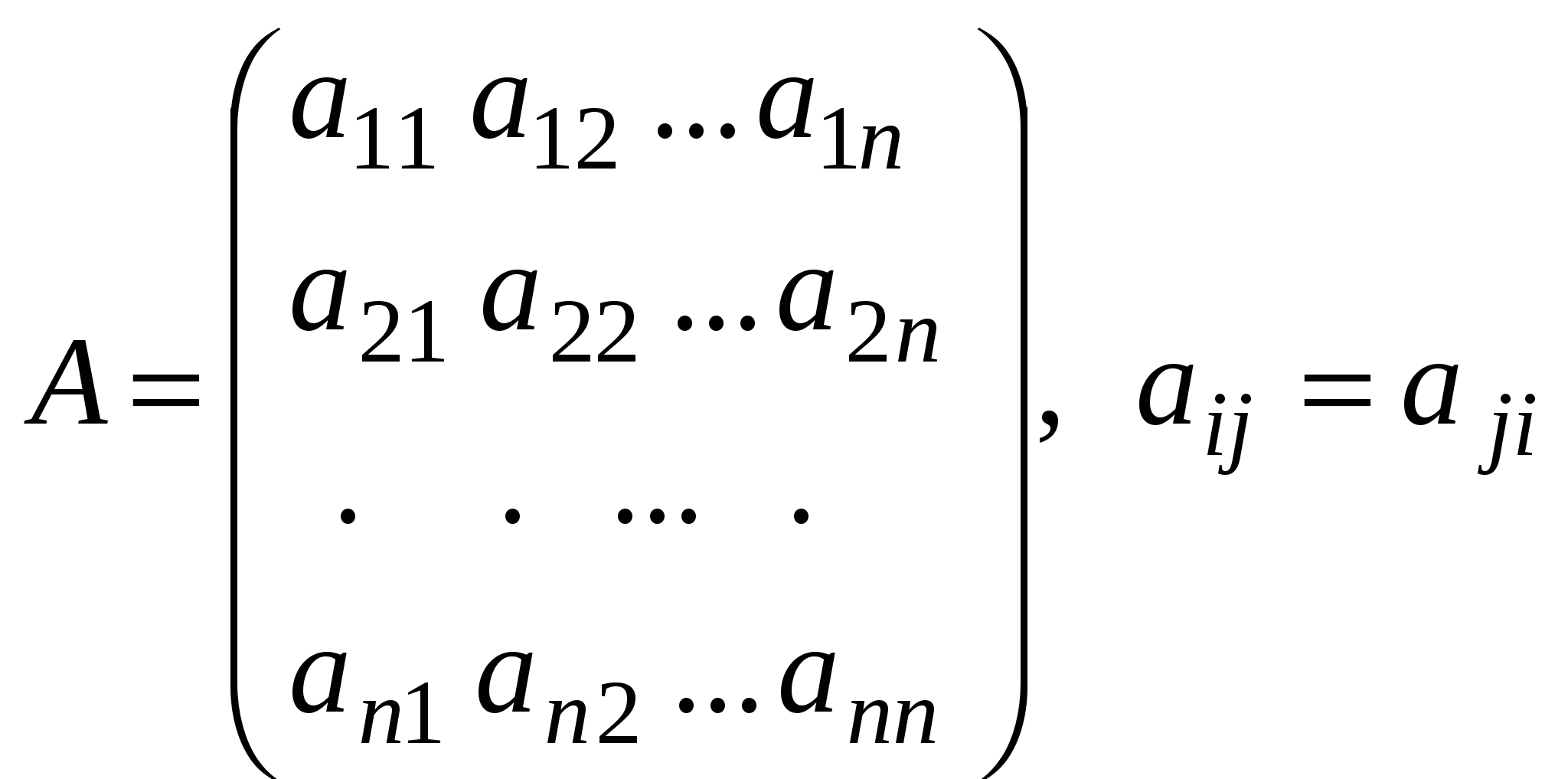 заданной квадратичной формы. заданной квадратичной формы.
Находятся собственные значения и собственные векторы  симметричной матрицы симметричной матрицы  , которую можно считать матрицей симметричного оператора , которую можно считать матрицей симметричного оператора  в ортонормированном базисе в ортонормированном базисе 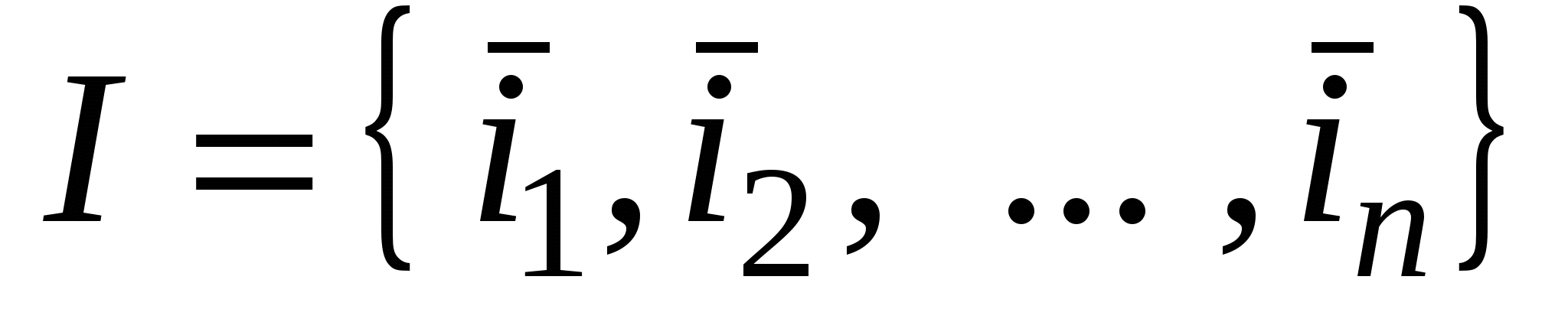 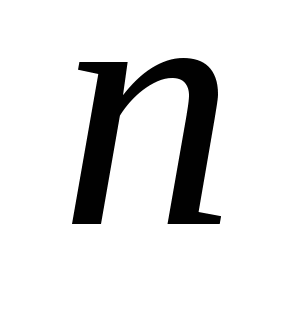 - мерного евклидова пространства - мерного евклидова пространства 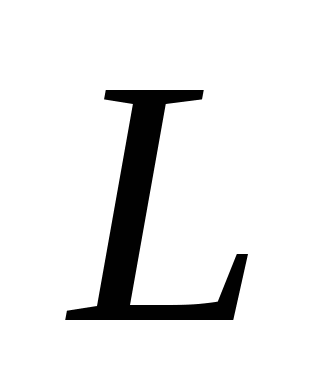 . .
По собственным векторам находится ортонормированный собственный базис  оператора оператора  и ортогональная матрица и ортогональная матрица 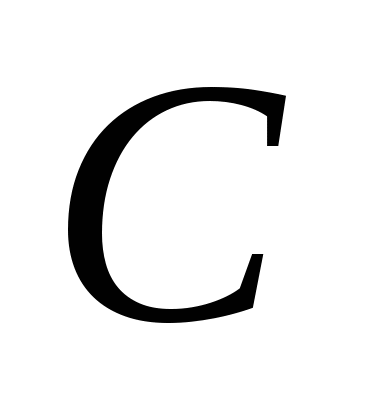 перехода от базиса перехода от базиса 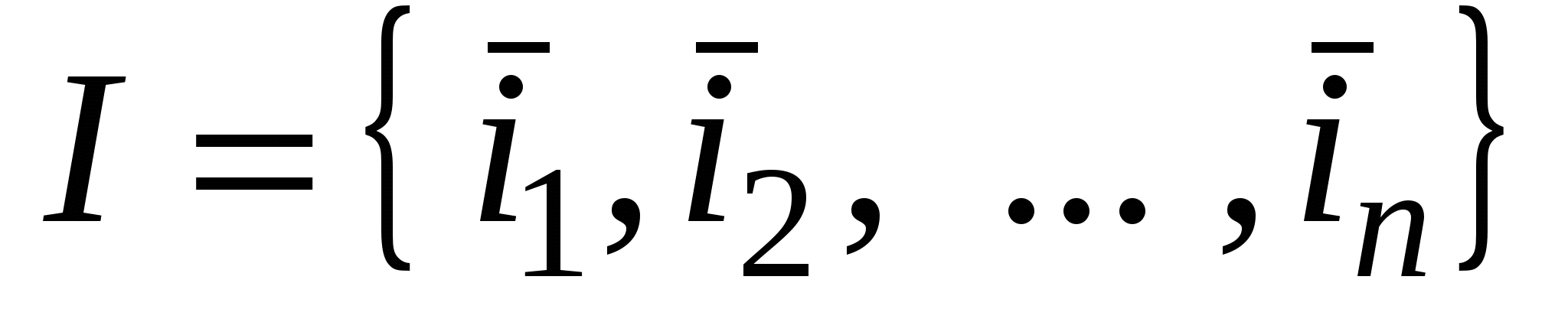 к базису к базису . .
В заданной квадратичной форме выполняется преобразование (1), в результате которого квадратичная форма принимает следующий канонический вид
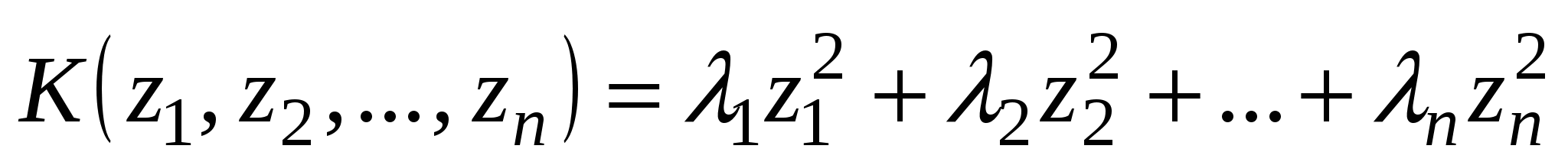 . (2) . (2)
Пример 1. Привести квадратичную форму 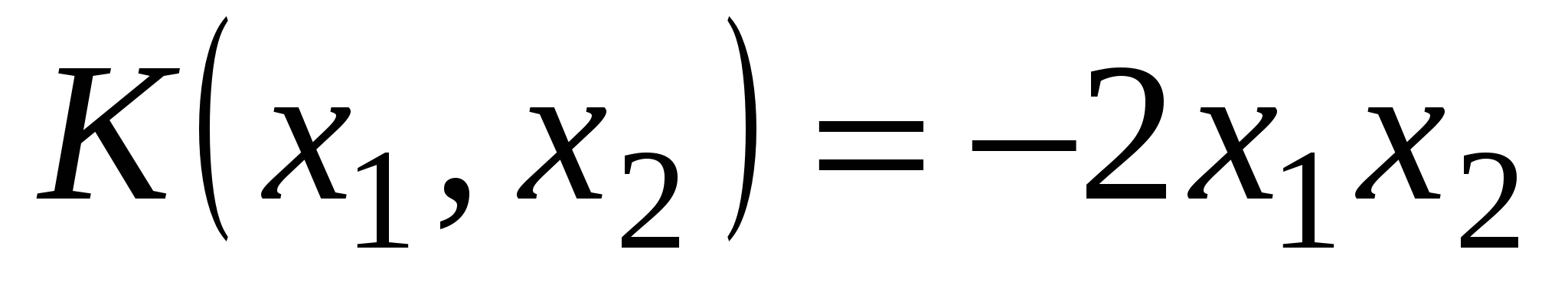 ортогональным преобразованием к каноническому виду. ортогональным преобразованием к каноническому виду.
Решение. Выполним все указанные выше шаги 1 – 4.
1. 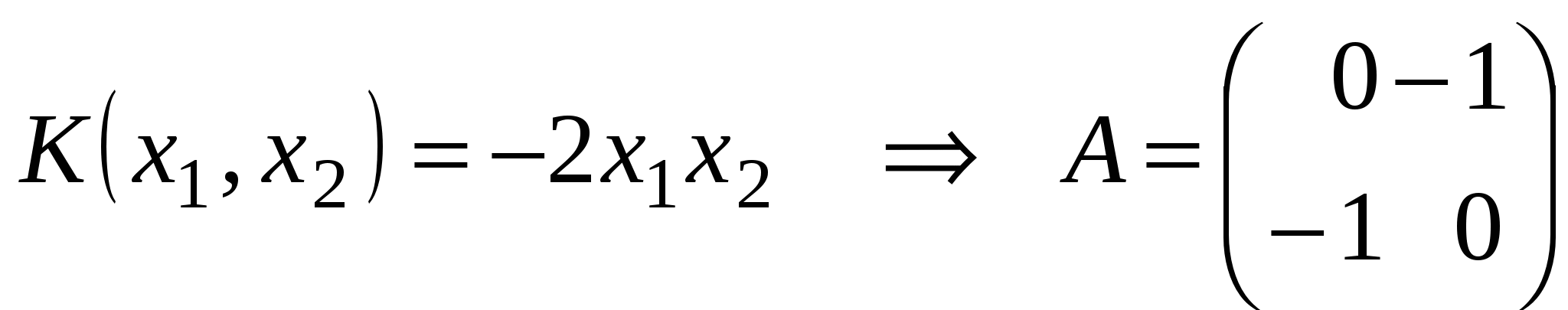 - матрица квадратичной формы. Эту матрицу можно считать матрицей симметричного оператора - матрица квадратичной формы. Эту матрицу можно считать матрицей симметричного оператора  в ортонормированном базисе в ортонормированном базисе 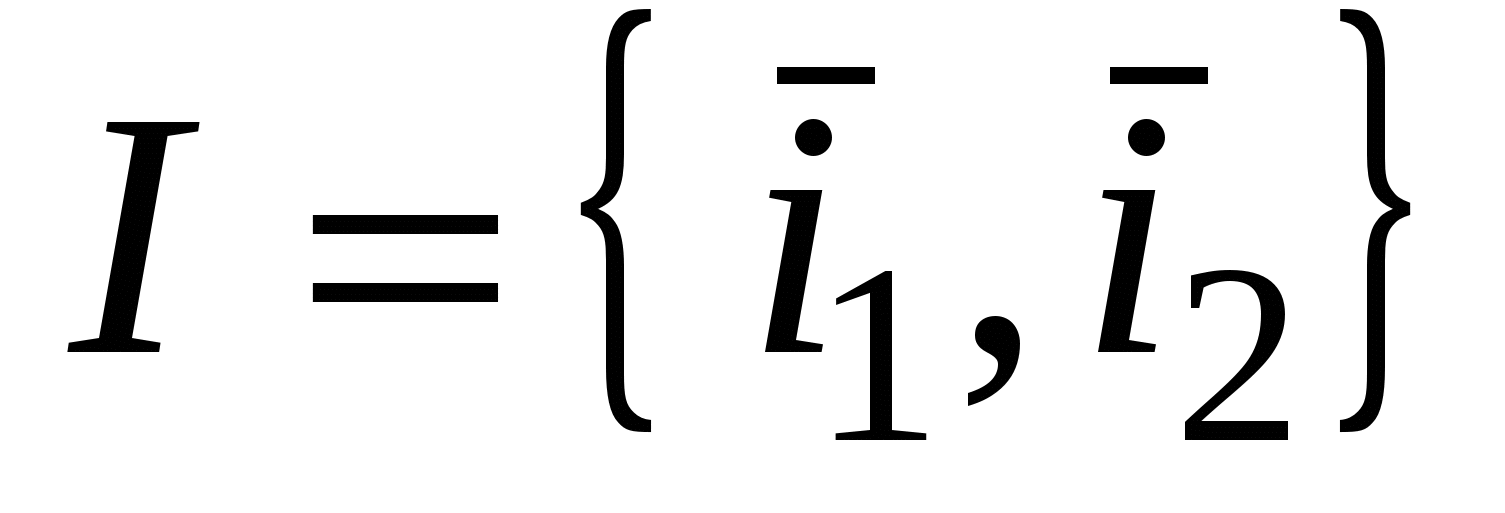 двумерного евклидова пространства двумерного евклидова пространства 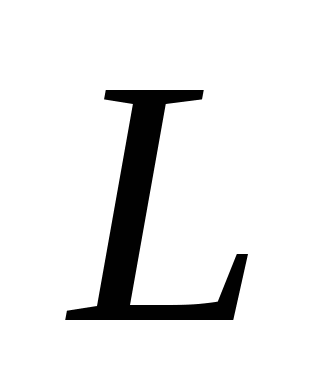 . .
2. 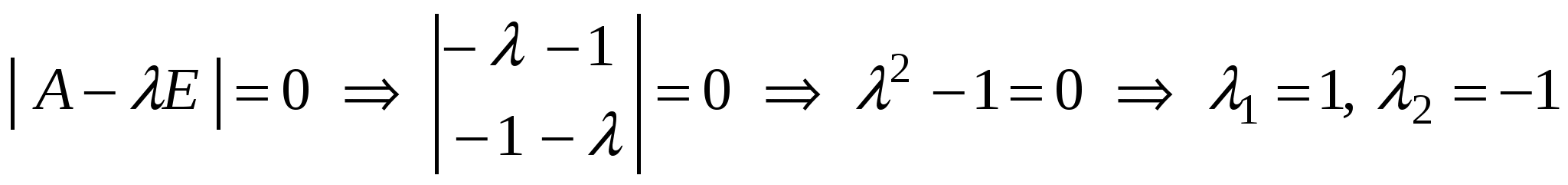 - собственные значения матрицы - собственные значения матрицы  . .
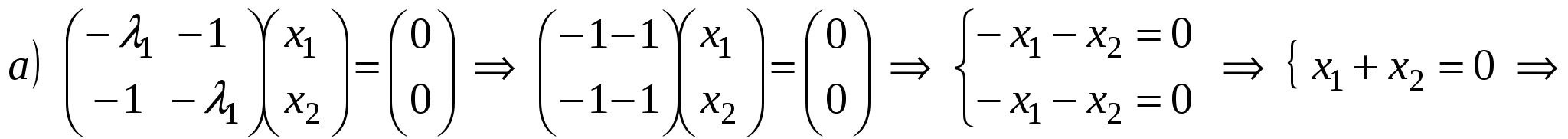
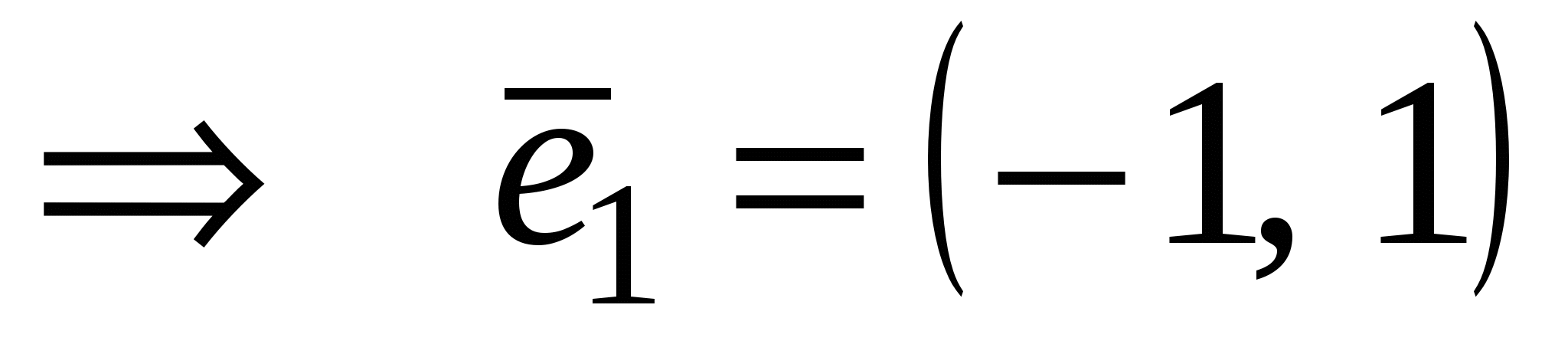 - собственный вектор с собственным значением - собственный вектор с собственным значением  . .
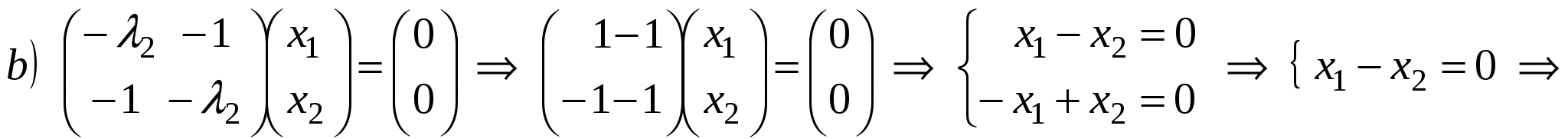
 - собственный вектор с собственным значением - собственный вектор с собственным значением  . .
3. Векторы  - собственные векторы с различными собственными значениями. Поэтому эти векторы ортогональны. Они образуют ортогональный базис пространства - собственные векторы с различными собственными значениями. Поэтому эти векторы ортогональны. Они образуют ортогональный базис пространства  . .
Нормируем эти векторы.
 . .
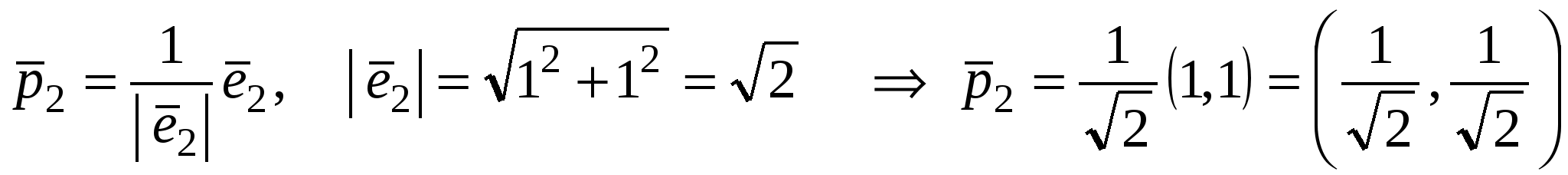 . .
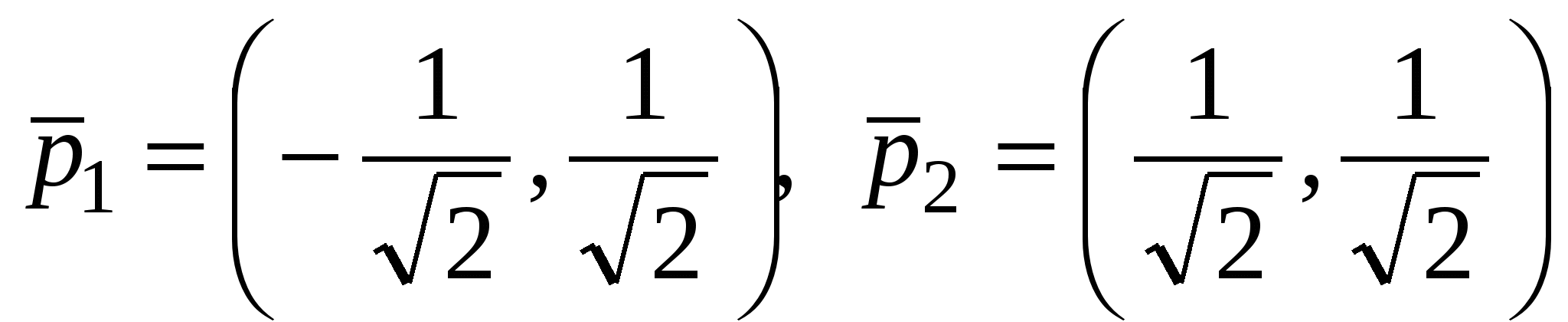 - собственный ортонормированный базис. - собственный ортонормированный базис.
Записывая координаты векторов в виде столбцов, получим следующую матрицу  перехода от ортонормированного базиса перехода от ортонормированного базиса 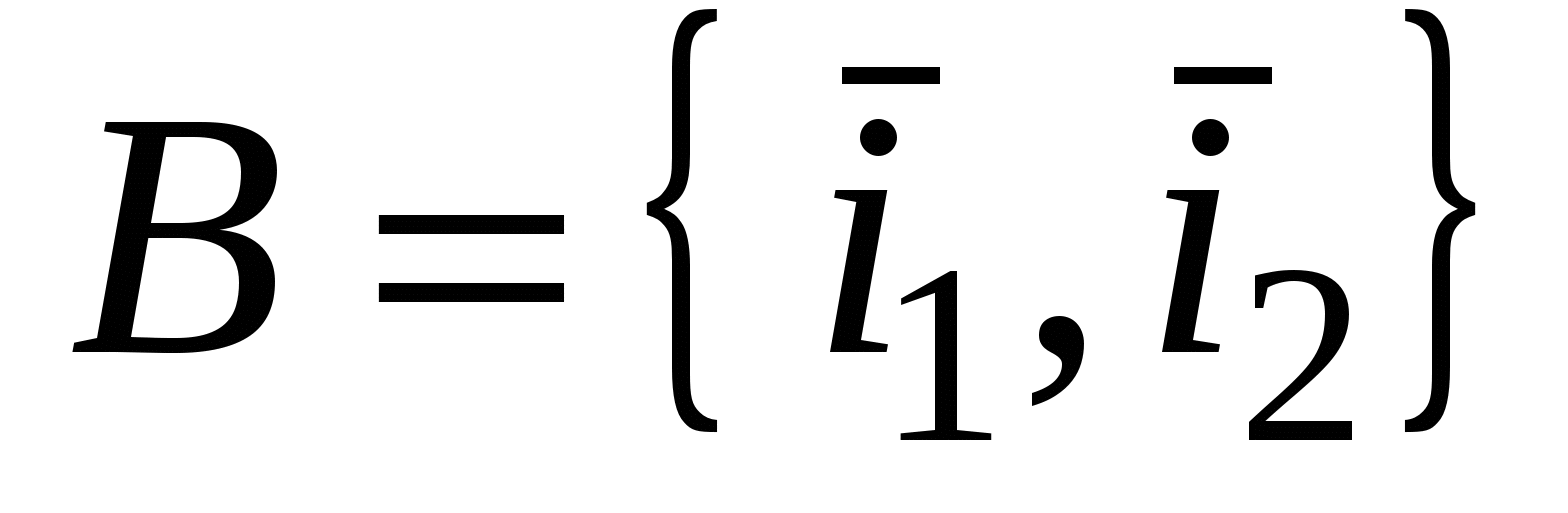 к ортонормированному базису к ортонормированному базису 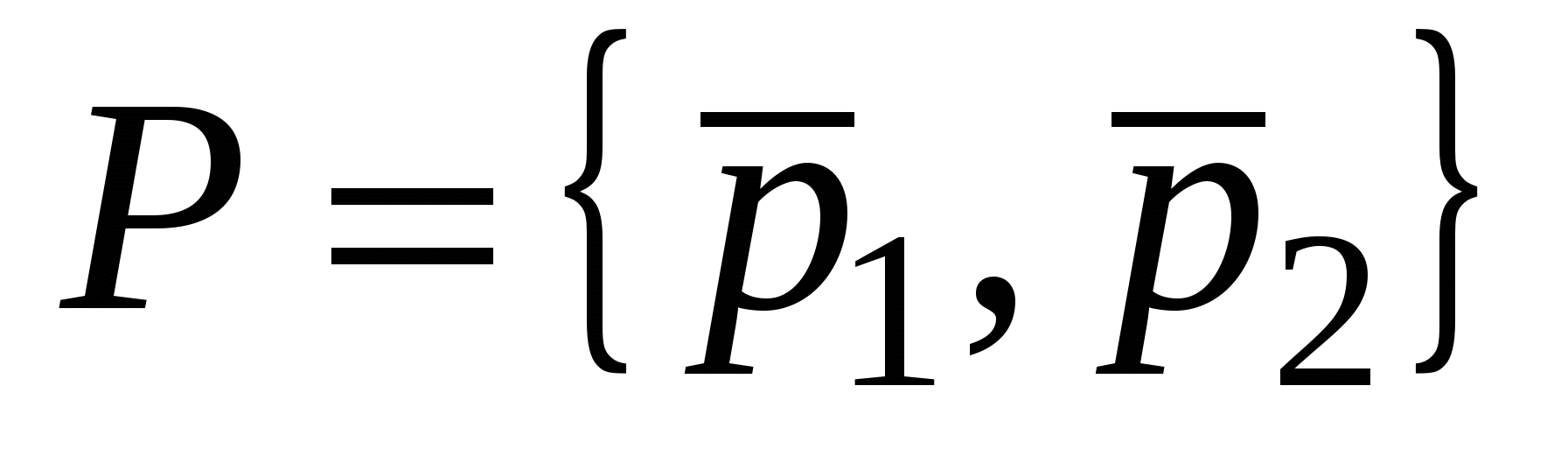 . .
 . .
Проверим на ортогональность матрицу 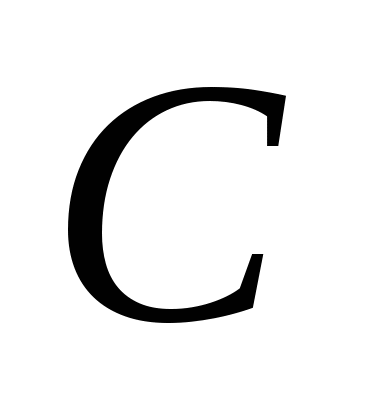 . .
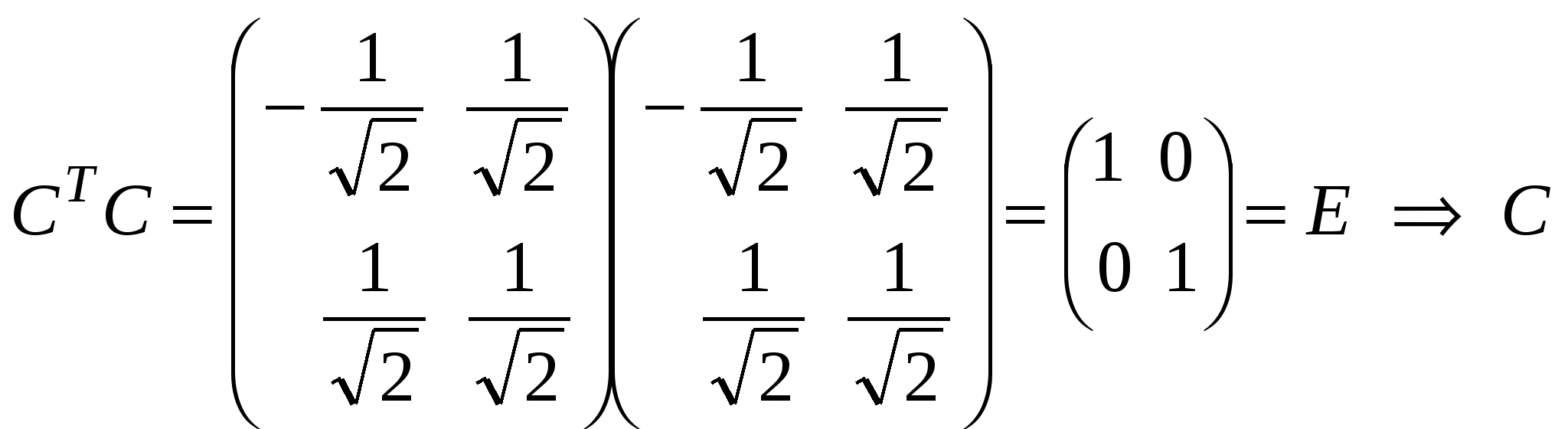 - ортогональная матрица. - ортогональная матрица.
4. Проведем в квадратичной форме ортогональное преобразование координат
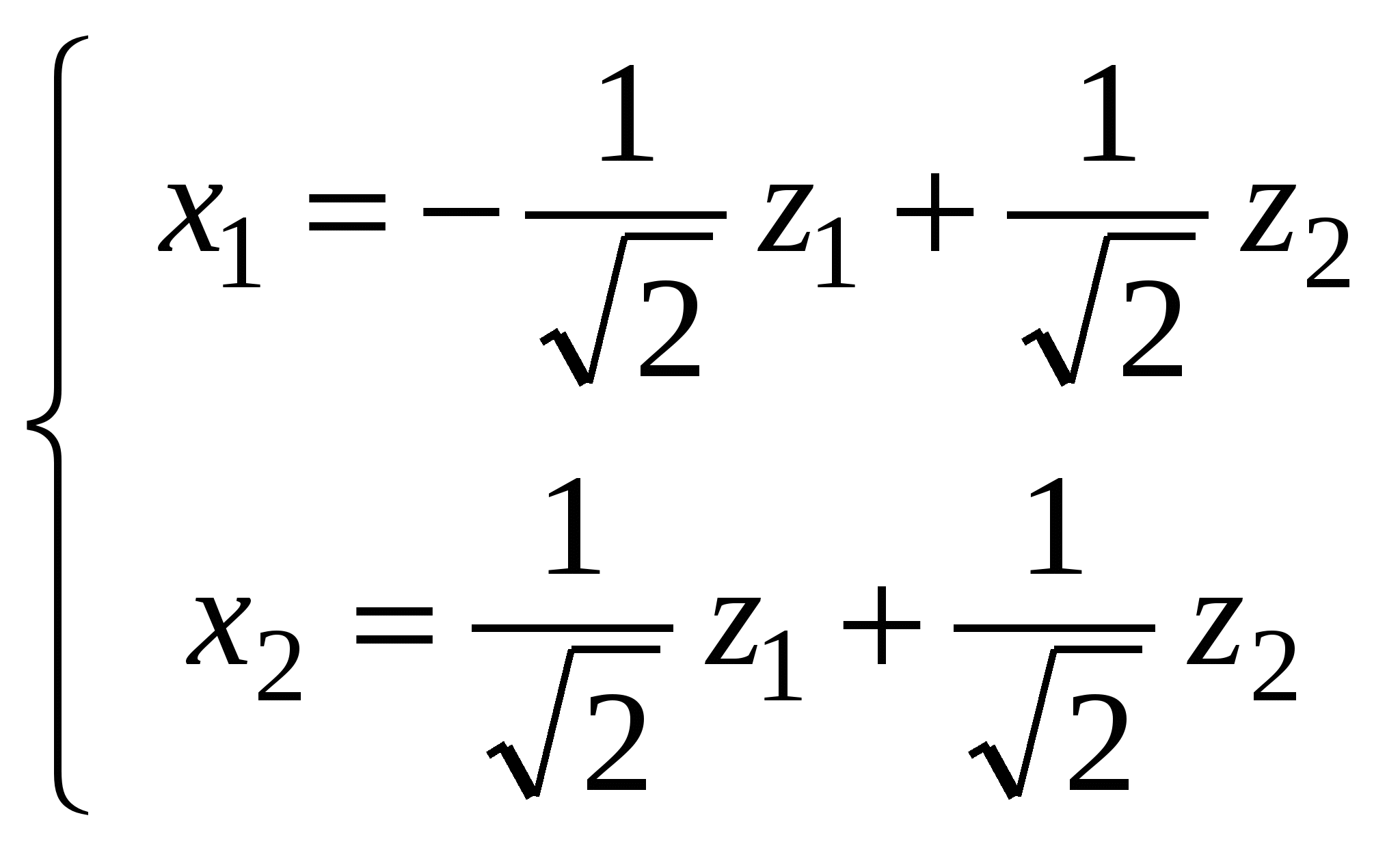 . (3) . (3)
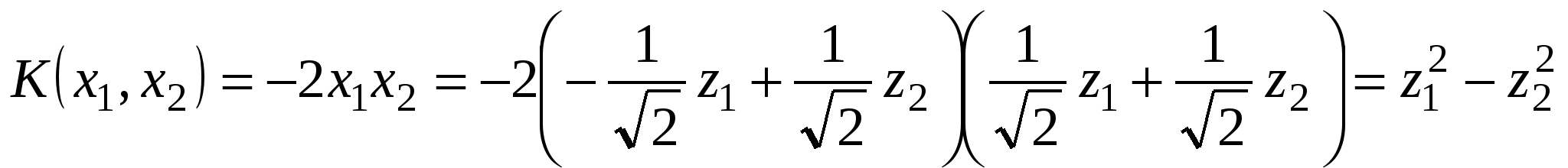 - канонический вид квадратичной формы, полученный ортогональным преобразованием координат (3). - канонический вид квадратичной формы, полученный ортогональным преобразованием координат (3).
Заметим, что ответ полностью согласуется с формулой (2).
Пример 2. Привести квадратичную форму

ортогональным преобразованием к каноническому виду.
Решение.
1. 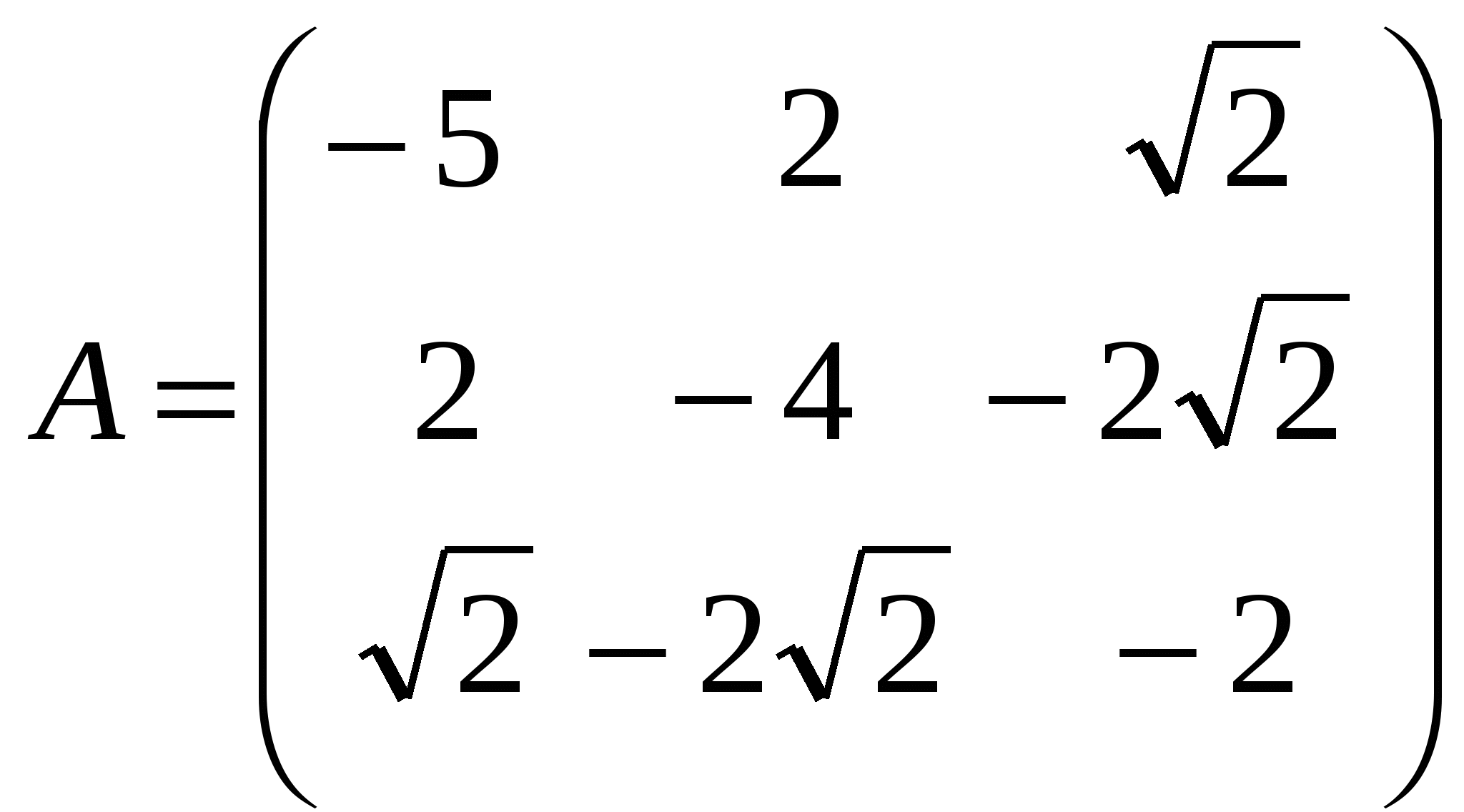 - матрица заданной квадратичной формы. - матрица заданной квадратичной формы.
2. 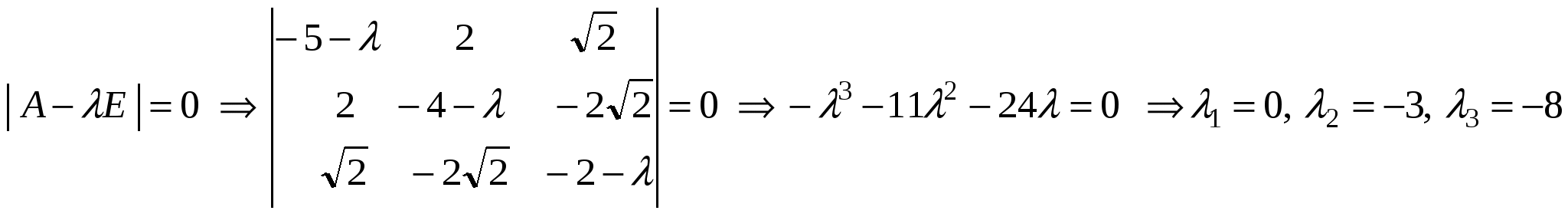 . .
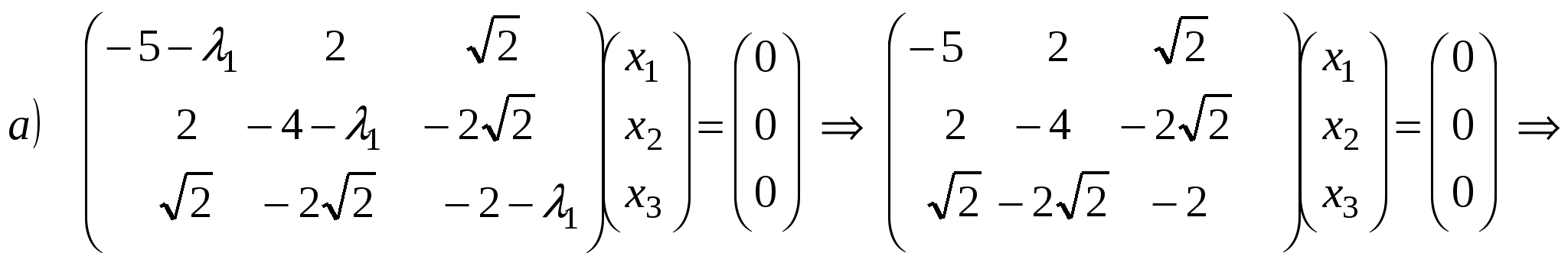
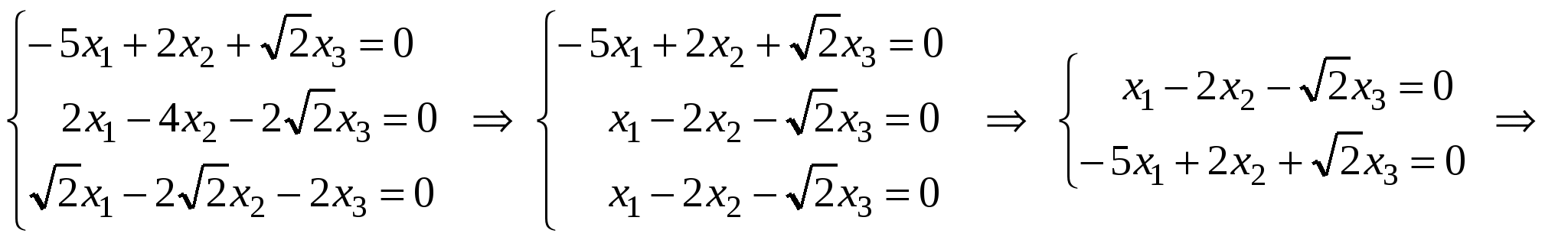

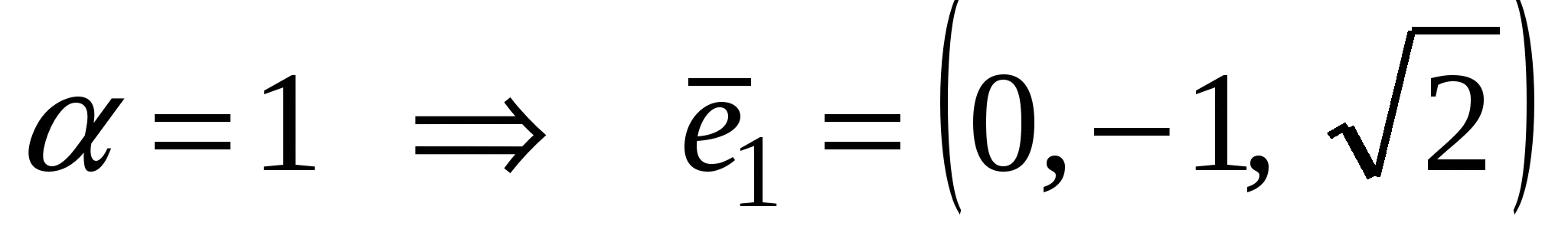 - собственный вектор с собственным значением - собственный вектор с собственным значением  . .

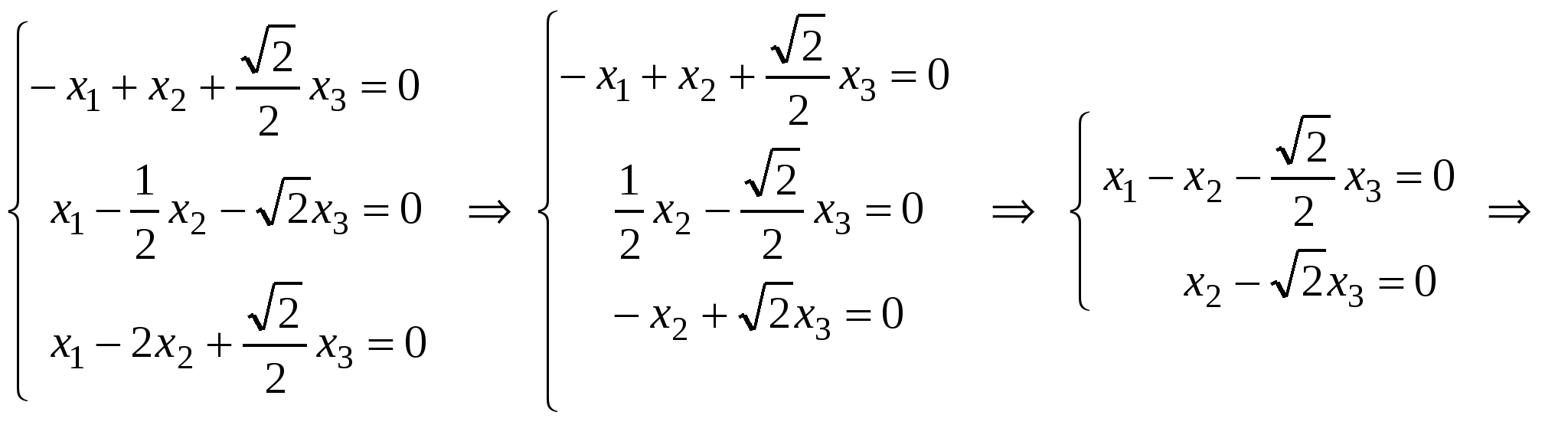
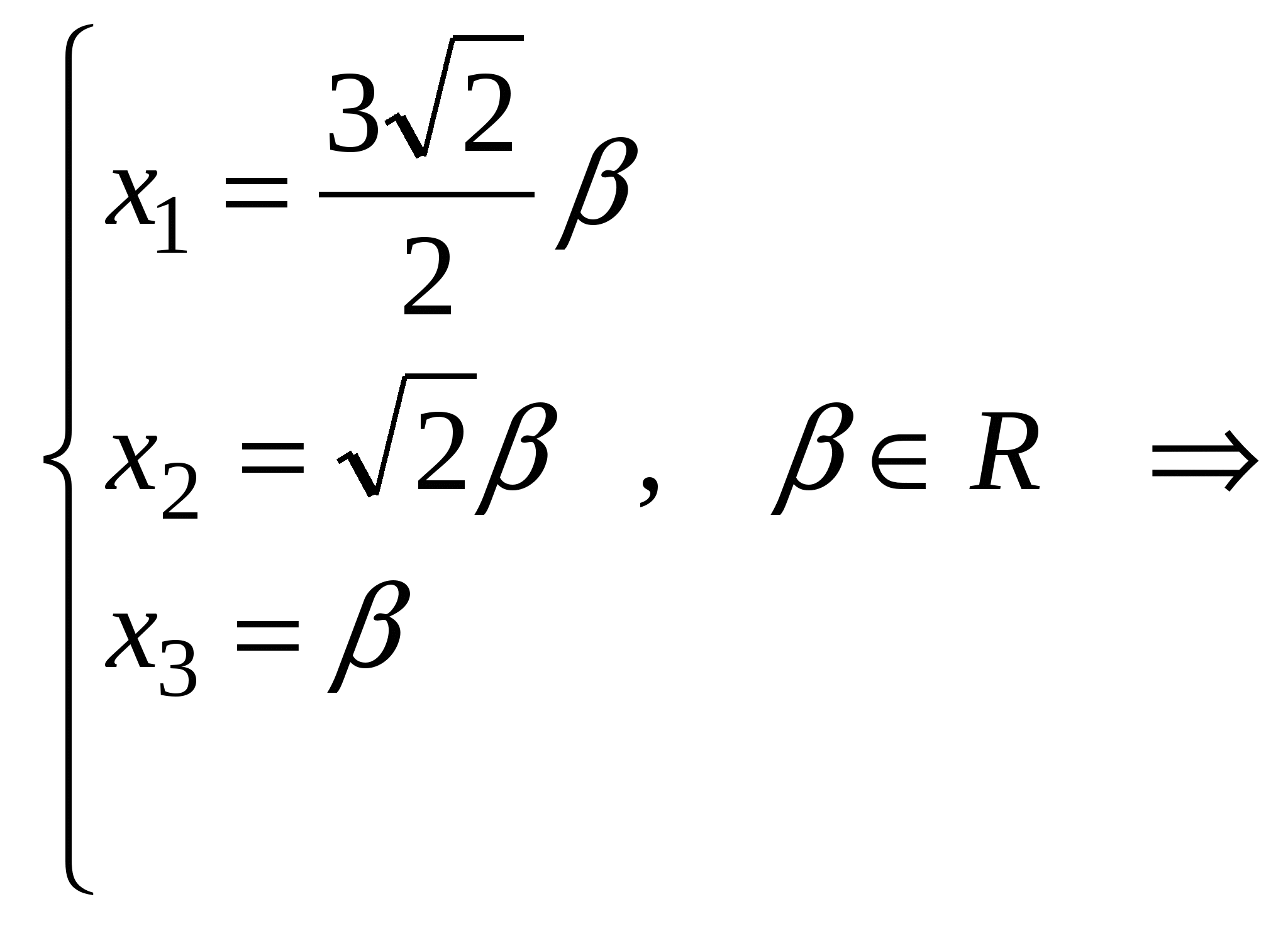
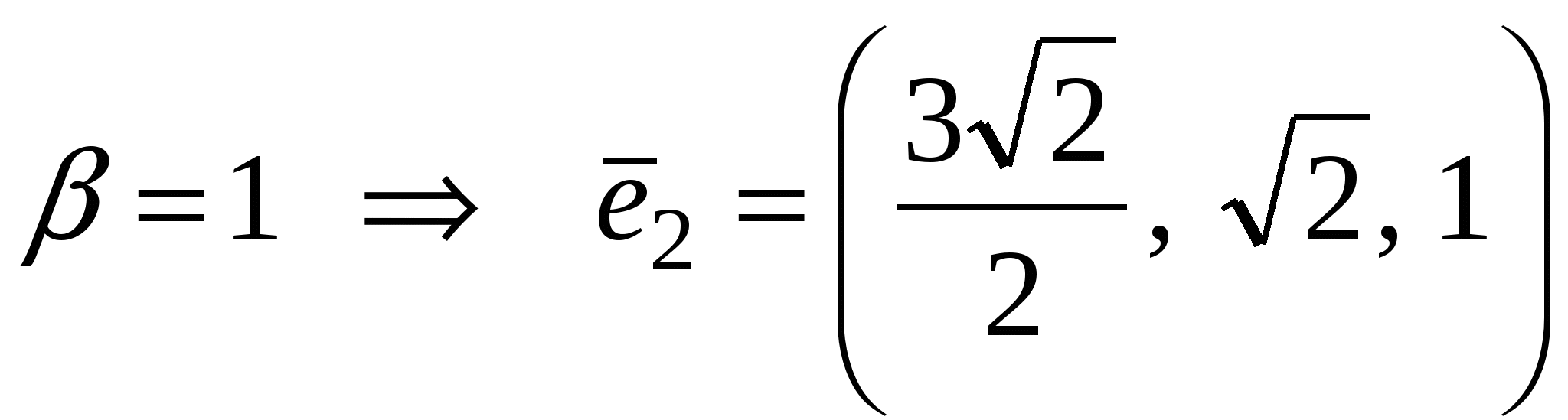 - собственный вектор с собственным значением - собственный вектор с собственным значением 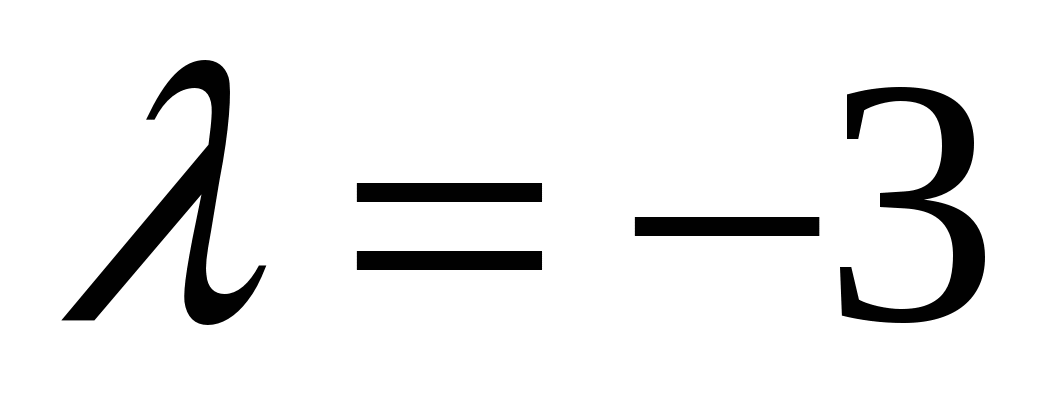 . .
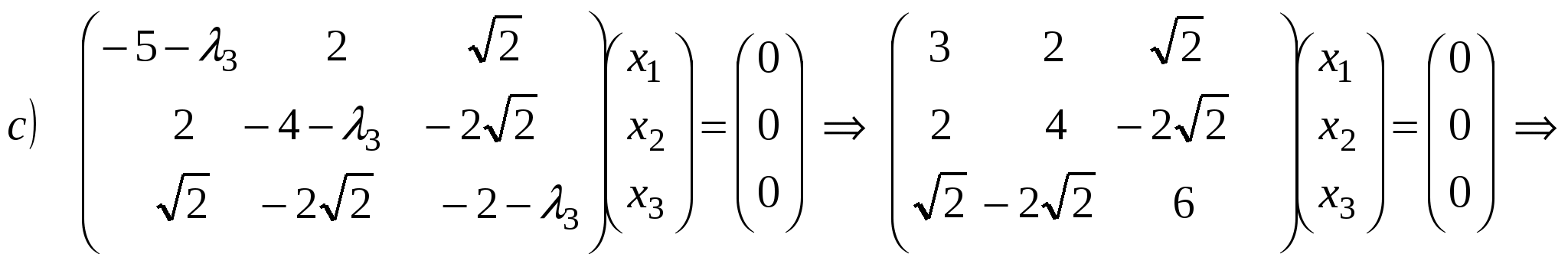
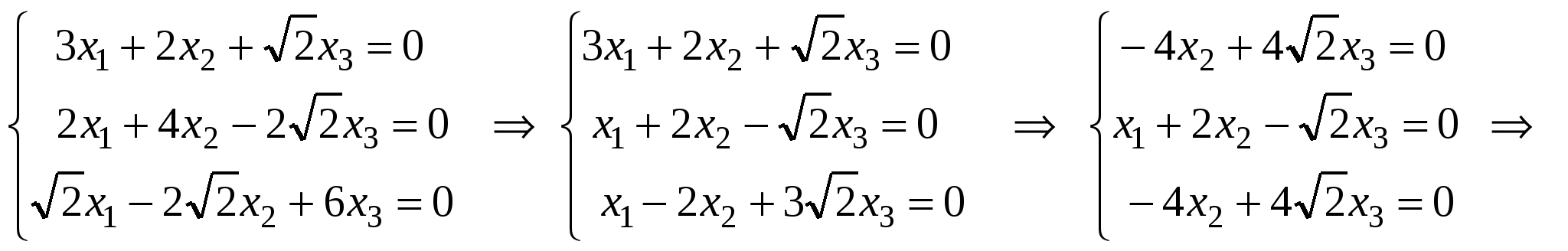

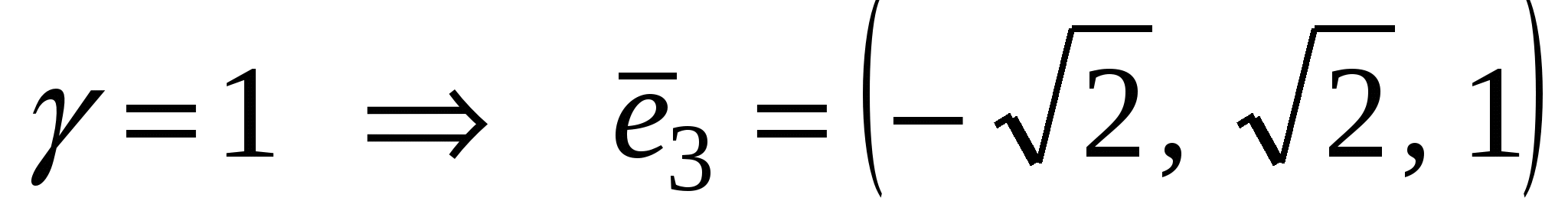 - собственный вектор с собственным значением - собственный вектор с собственным значением 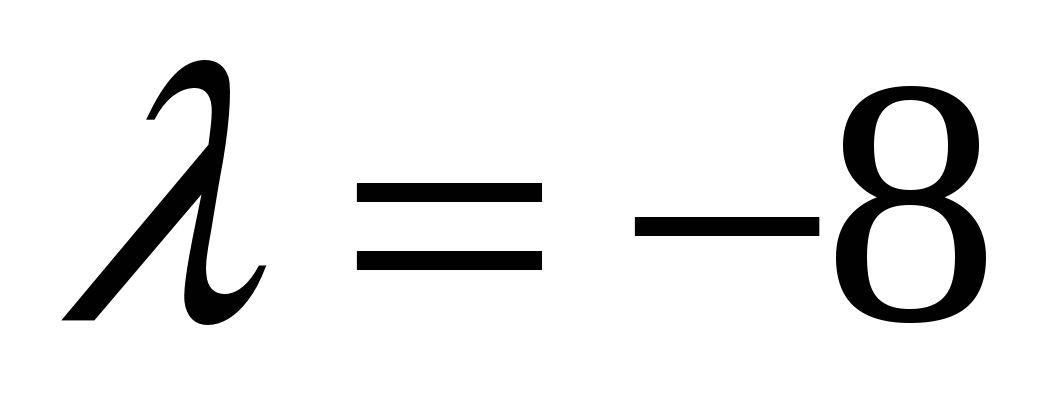 . .
3. 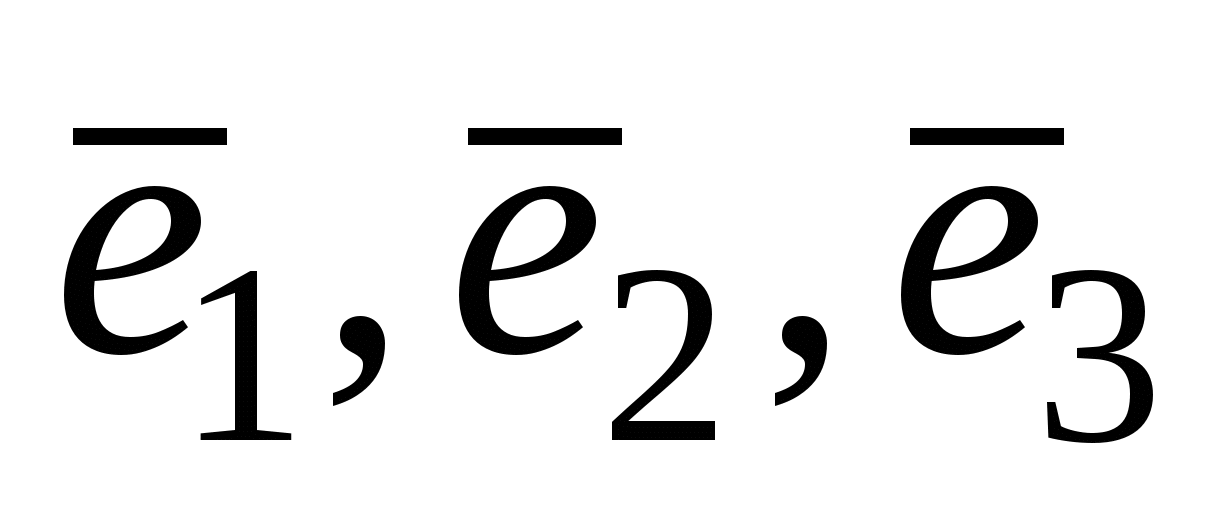 - собственные векторы с различными собственными значениями - собственные векторы с различными собственными значениями  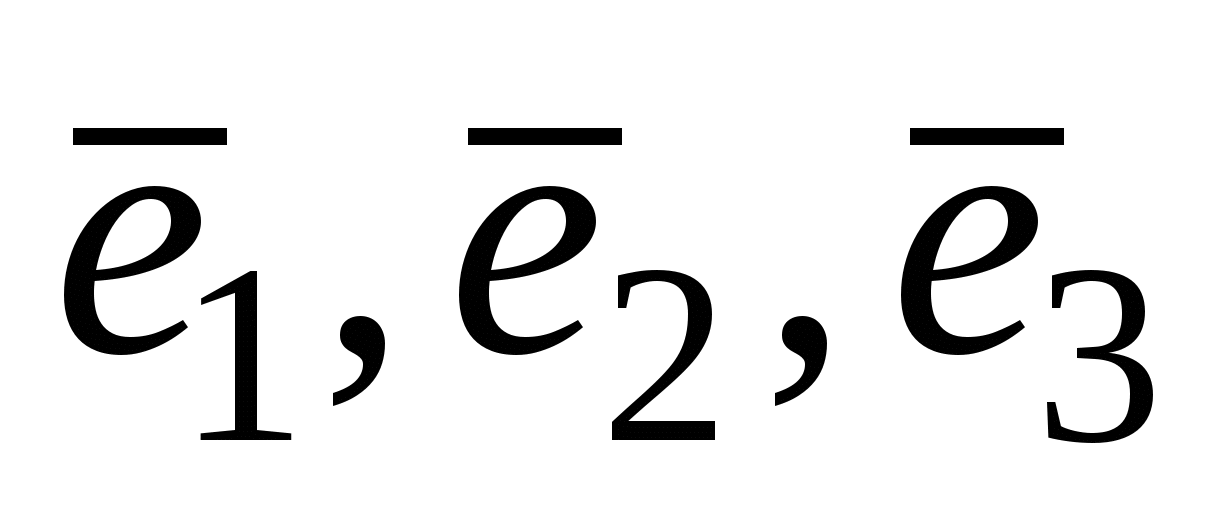 - ортогональный собственный базис. - ортогональный собственный базис.
Нормируем векторы 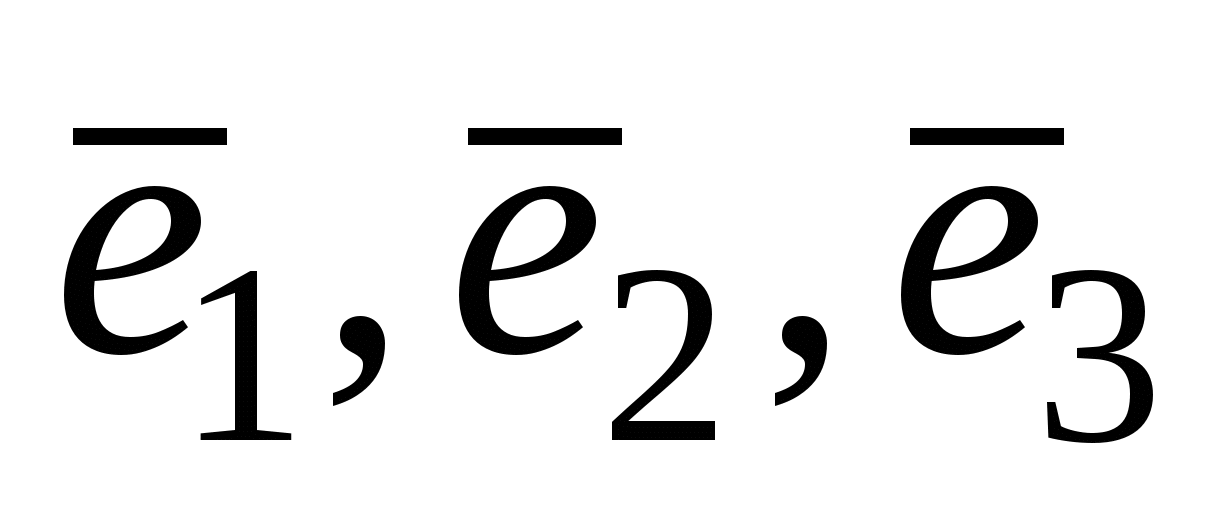 . .
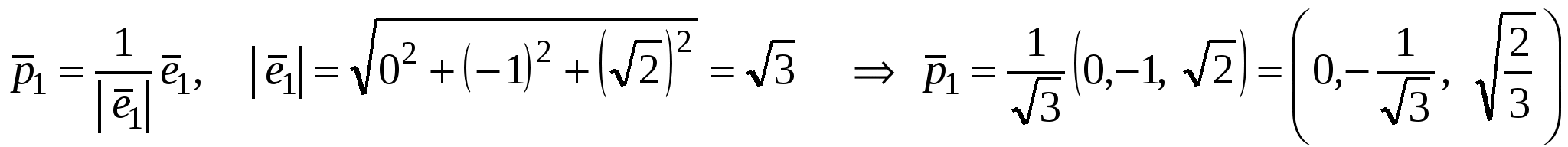  . .
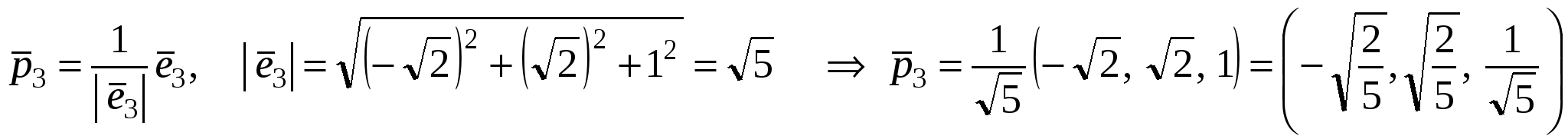 . .
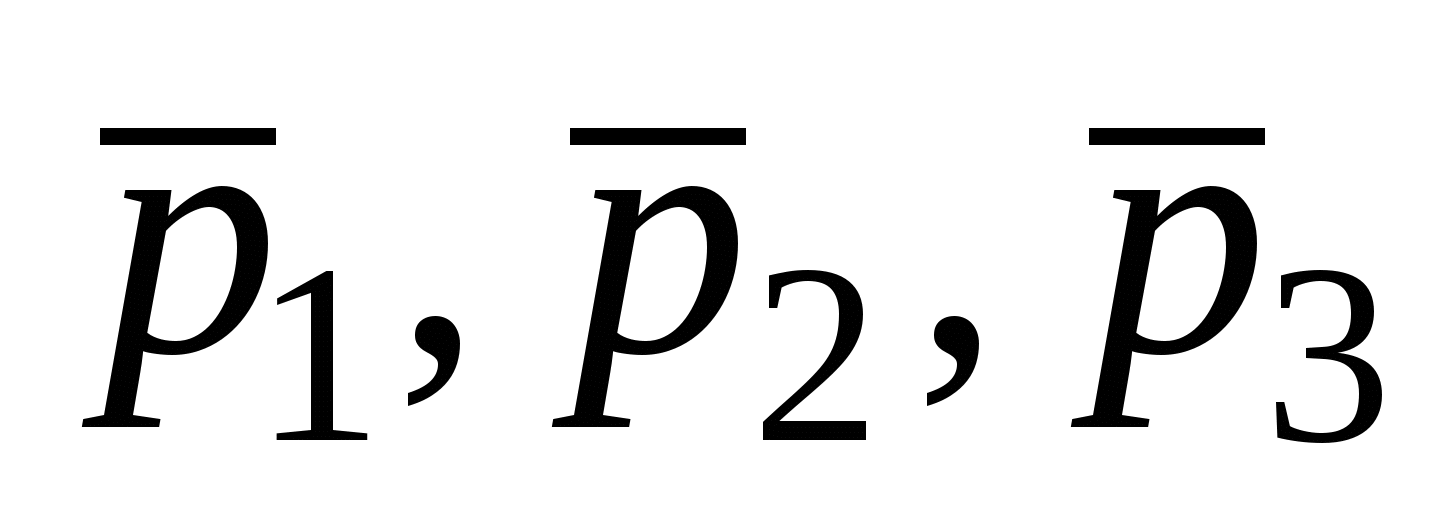 - ортонормированный собственный базис. - ортонормированный собственный базис.
По координатам векторов 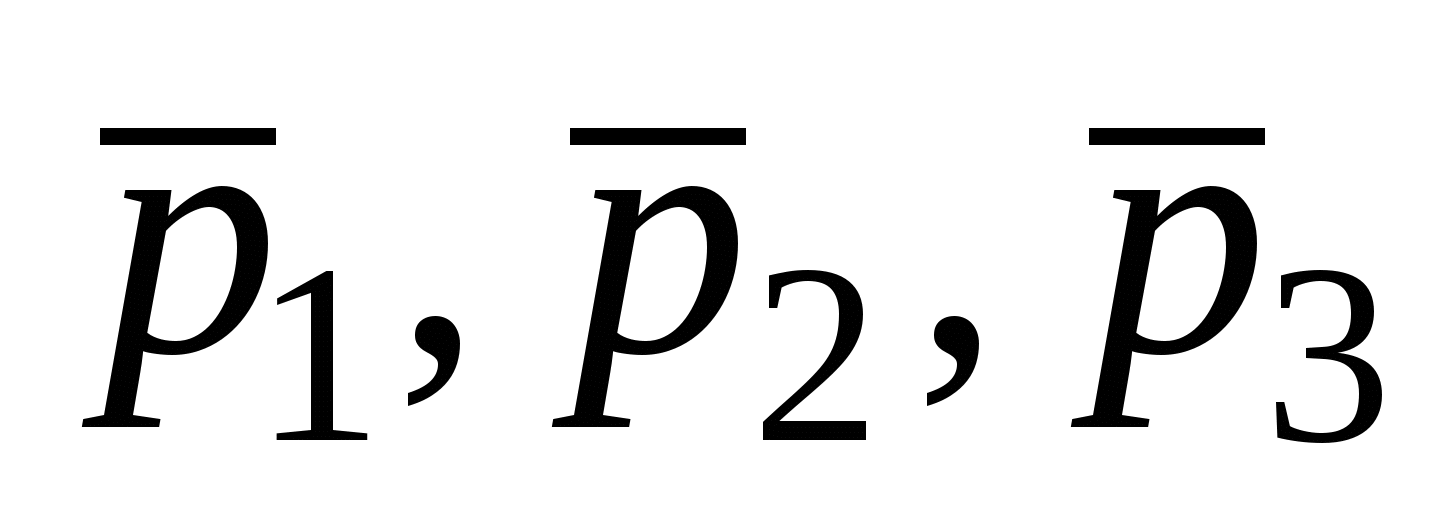 находим матрицу находим матрицу 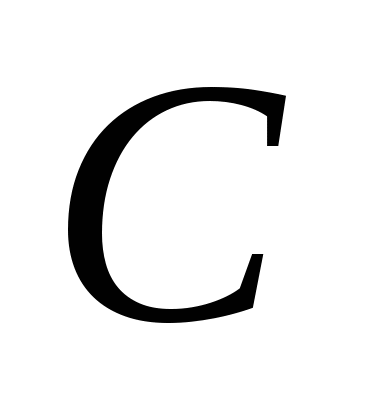 ортогонального преобразования координат и само это преобразование. ортогонального преобразования координат и само это преобразование.
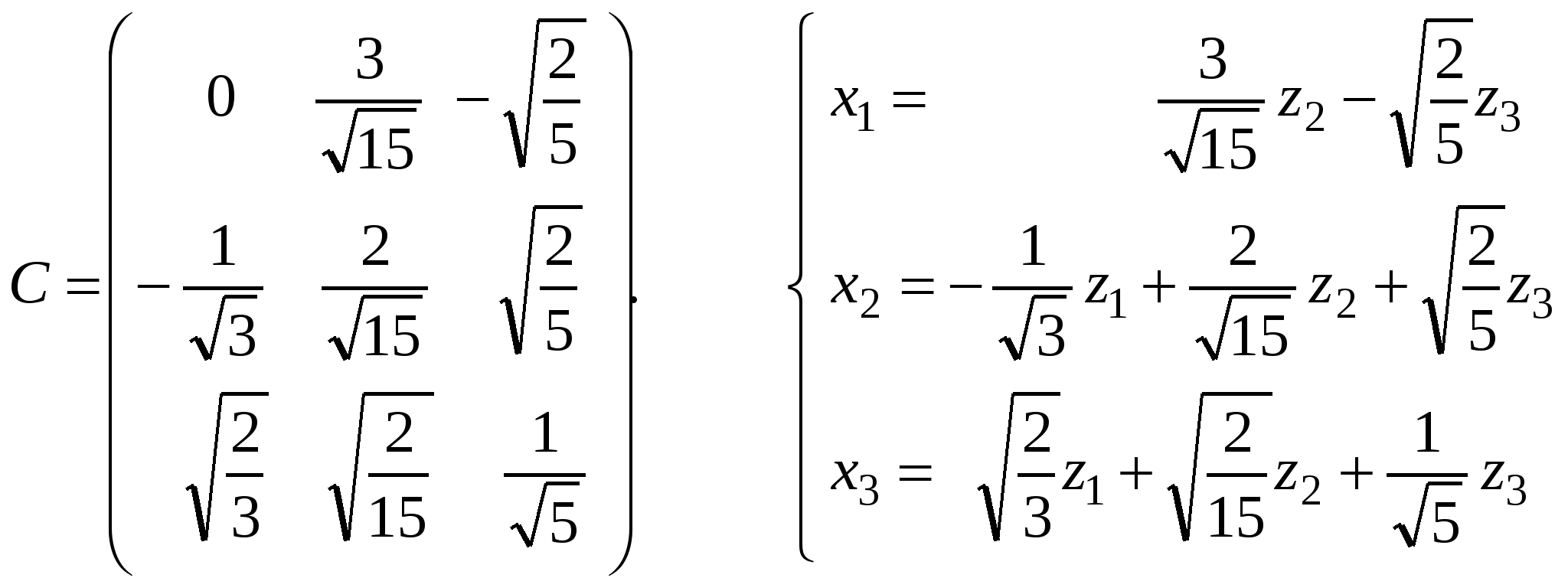 . .
4. Используя найденное преобразование координат приводим квадратичную форму к каноническому виду.
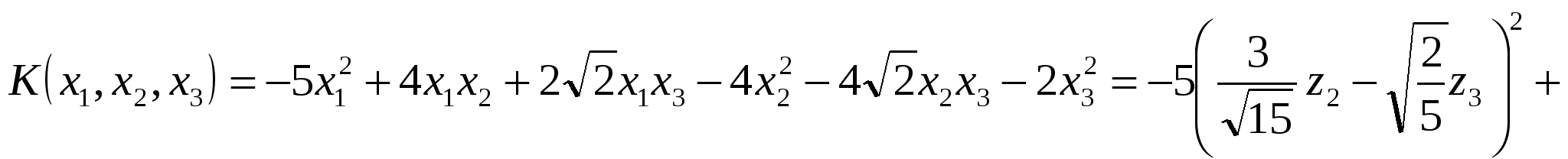

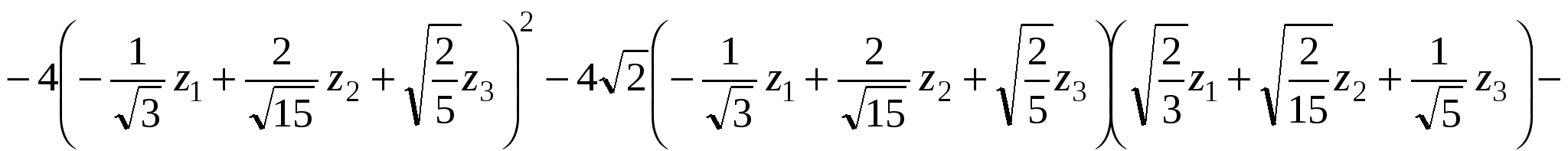
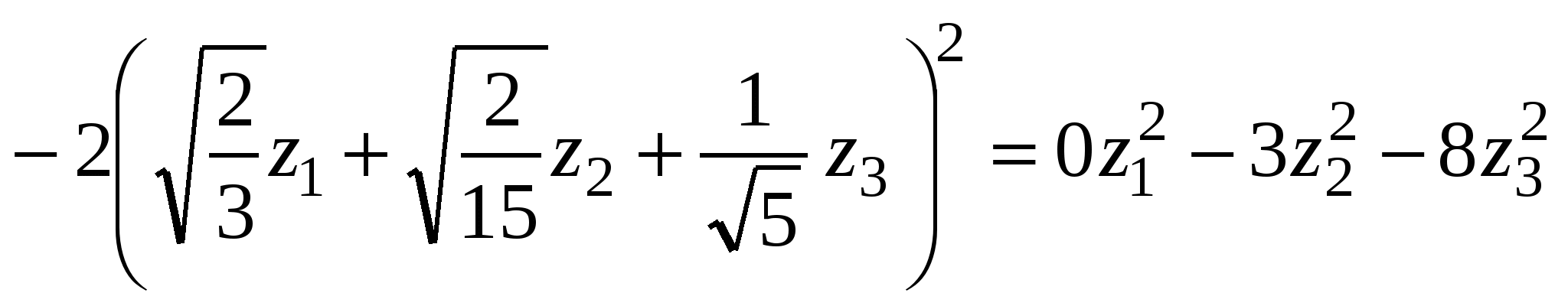 . .
Пример 3. Привести квадратичную форму
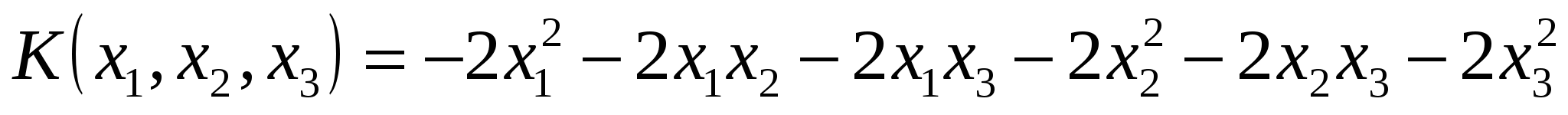
ортогональным преобразованием к каноническому виду.
Решение.
1. 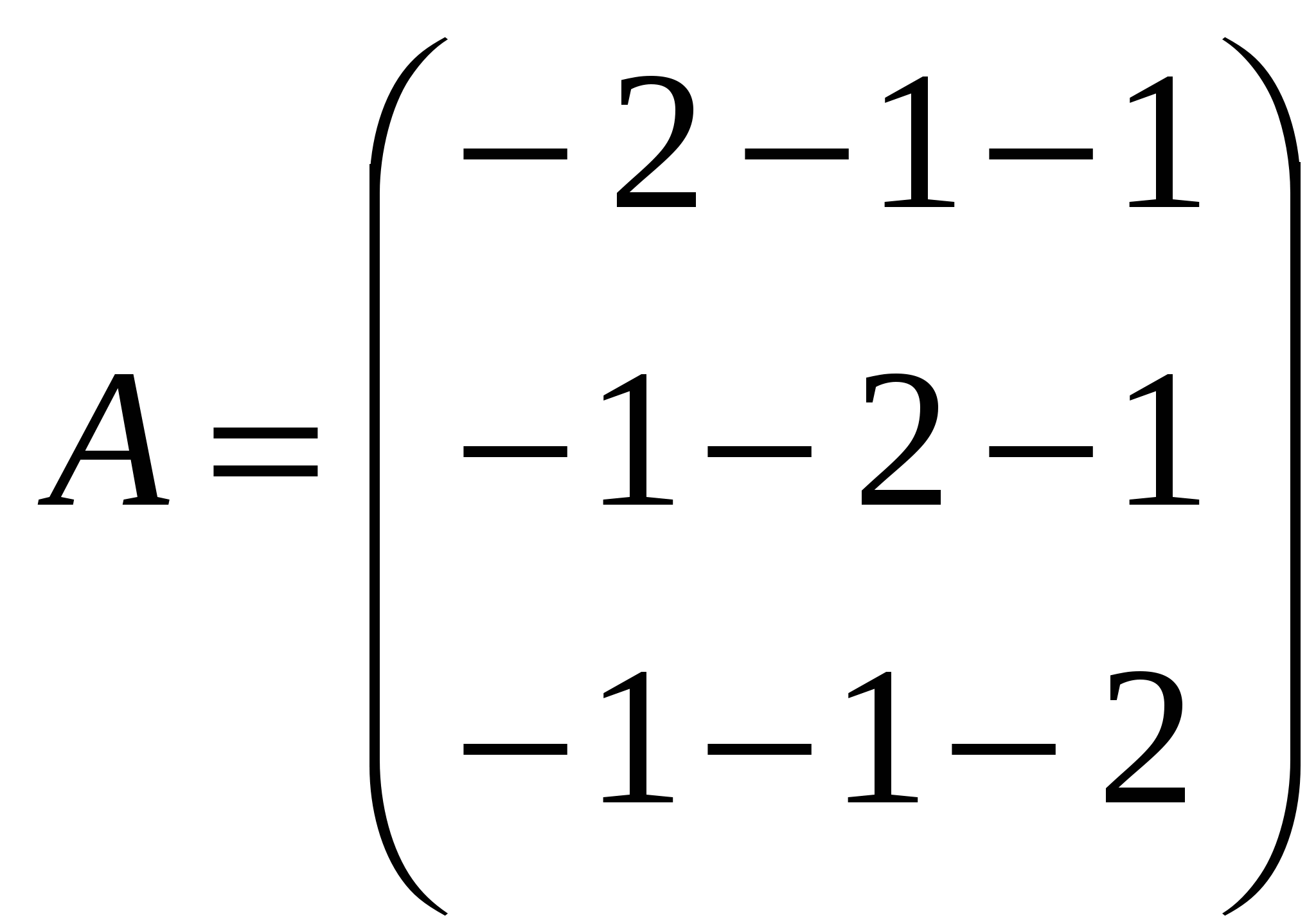 - матрица заданной квадратичной формы. Эту матрицу можно считать матрицей симметричного оператора - матрица заданной квадратичной формы. Эту матрицу можно считать матрицей симметричного оператора  в ортонормированном базисе в ортонормированном базисе 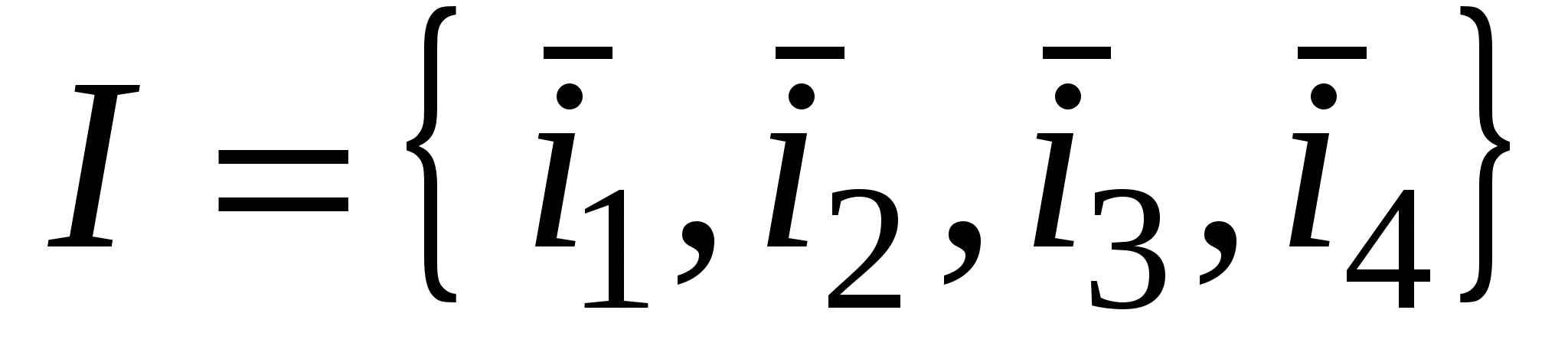 трехмерного евклидова пространства трехмерного евклидова пространства 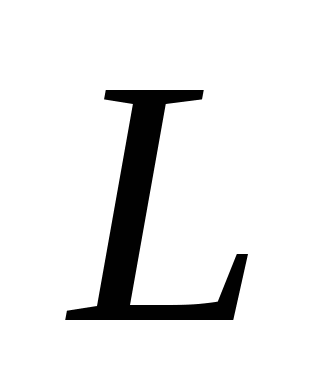 . .
2. 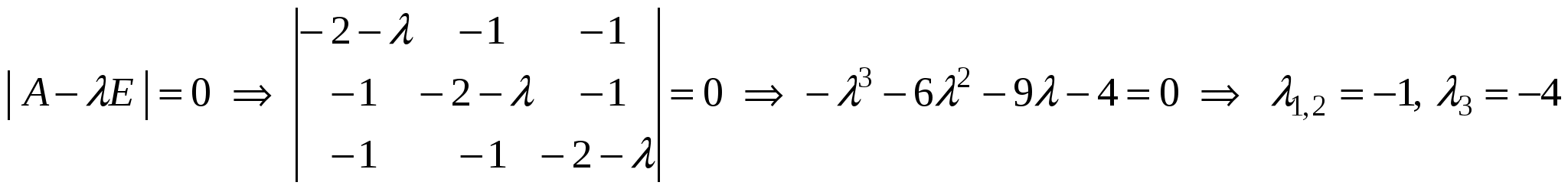 . .
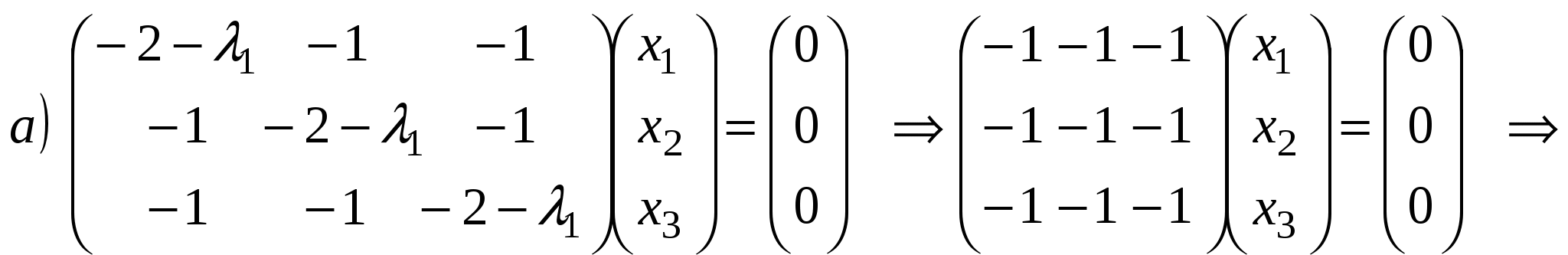

 . .
 . .
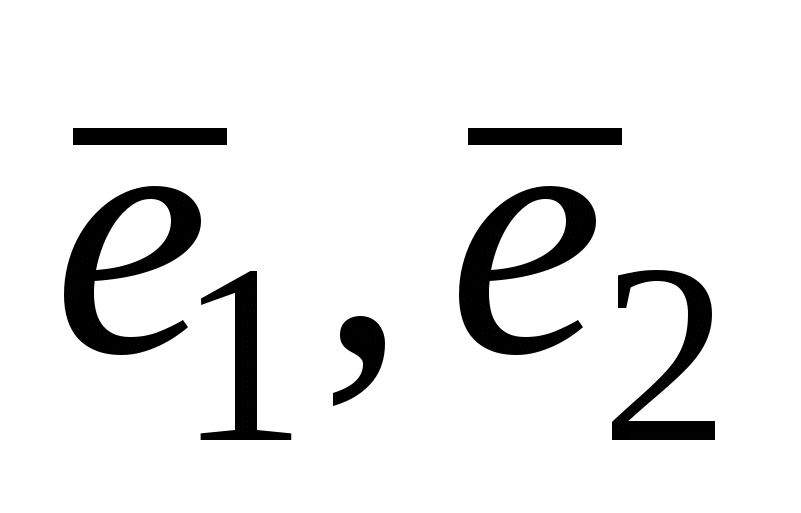 - два линейно независимых собственных вектора с собственным значением - два линейно независимых собственных вектора с собственным значением  . .
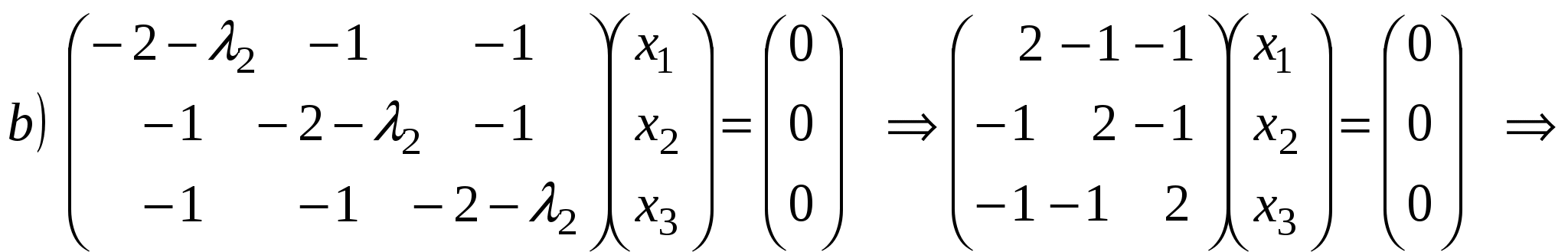

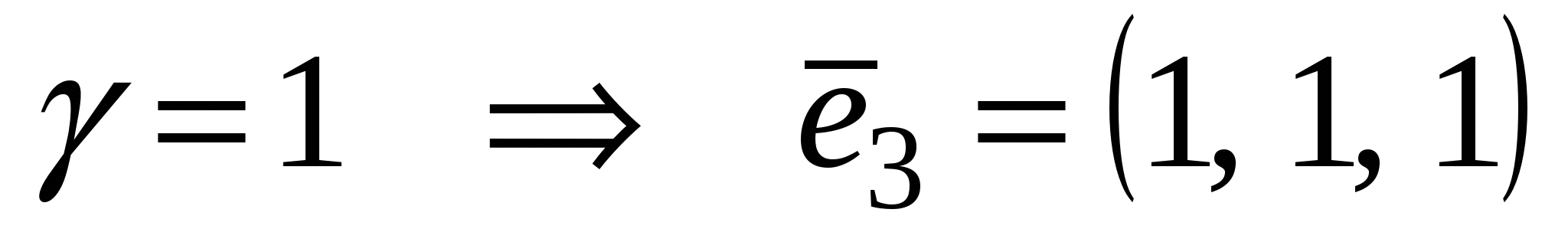 . .
3. 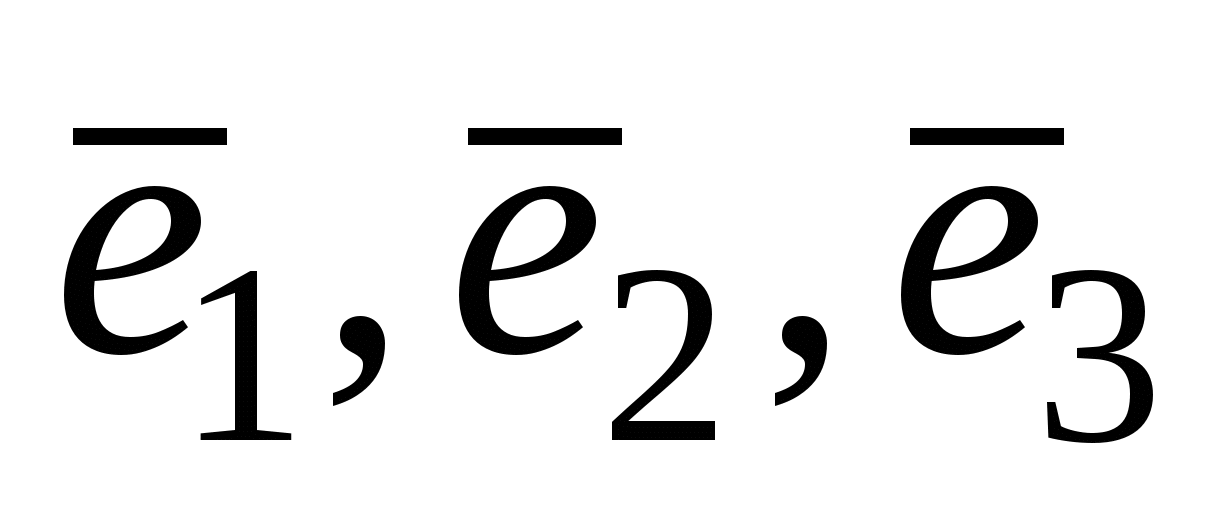 - собственный базис. Он не является ортогональным, т.к. - собственный базис. Он не является ортогональным, т.к. 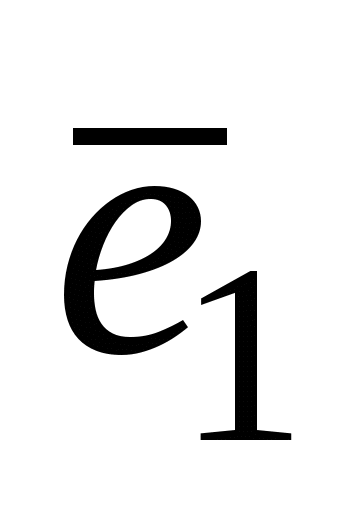 не ортогонален вектору не ортогонален вектору  . Проведем процесс ортогонализации к системе векторов . Проведем процесс ортогонализации к системе векторов 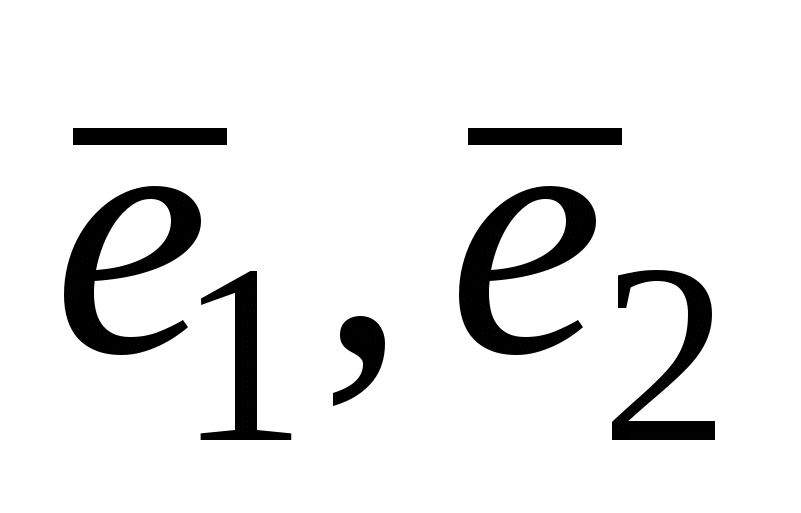 . .
 . .
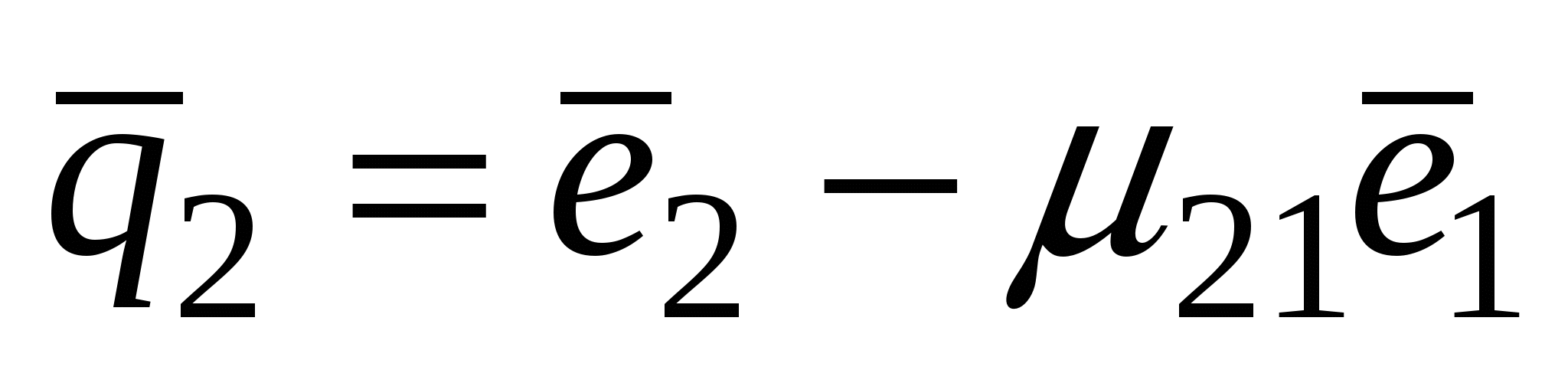 , ,  . .
Векторы 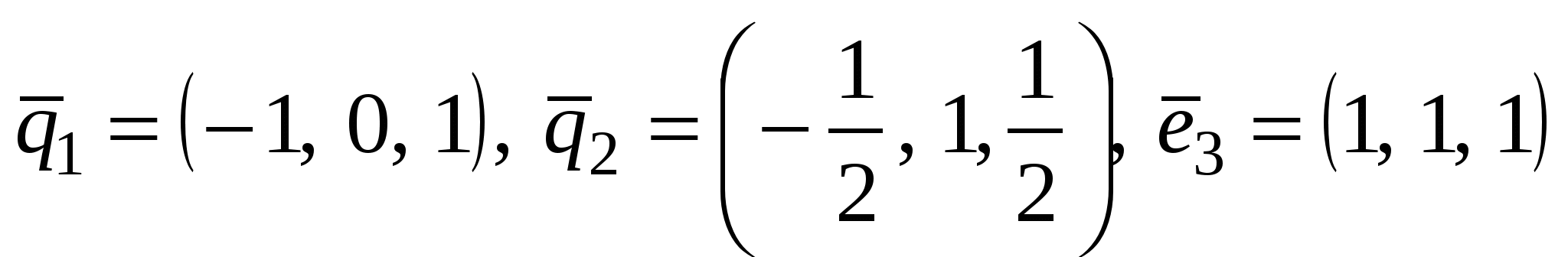 образуют собственный ортогональный базис симметричного оператора образуют собственный ортогональный базис симметричного оператора  . Пронормировав векторы . Пронормировав векторы 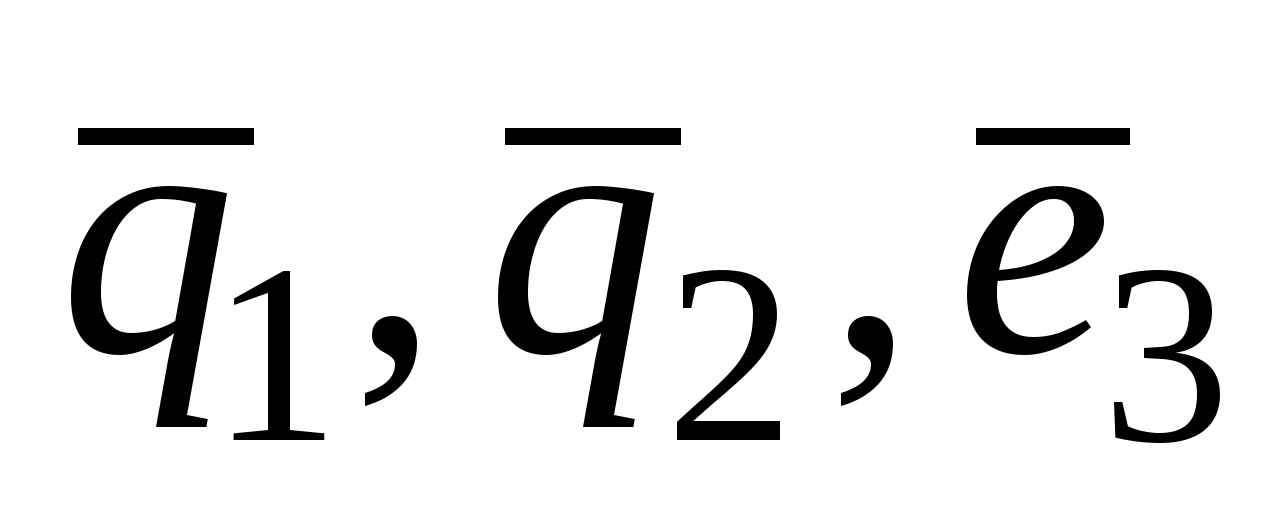 , получим собственный ортонормированный базис , получим собственный ортонормированный базис  . .
 . .
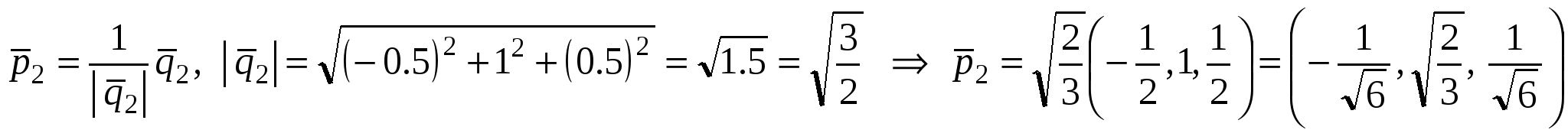 . .
 . .
4. По координатам векторов  находим матрицу ортогонального преобразования и само ортогональное преобразование координат. находим матрицу ортогонального преобразования и само ортогональное преобразование координат.
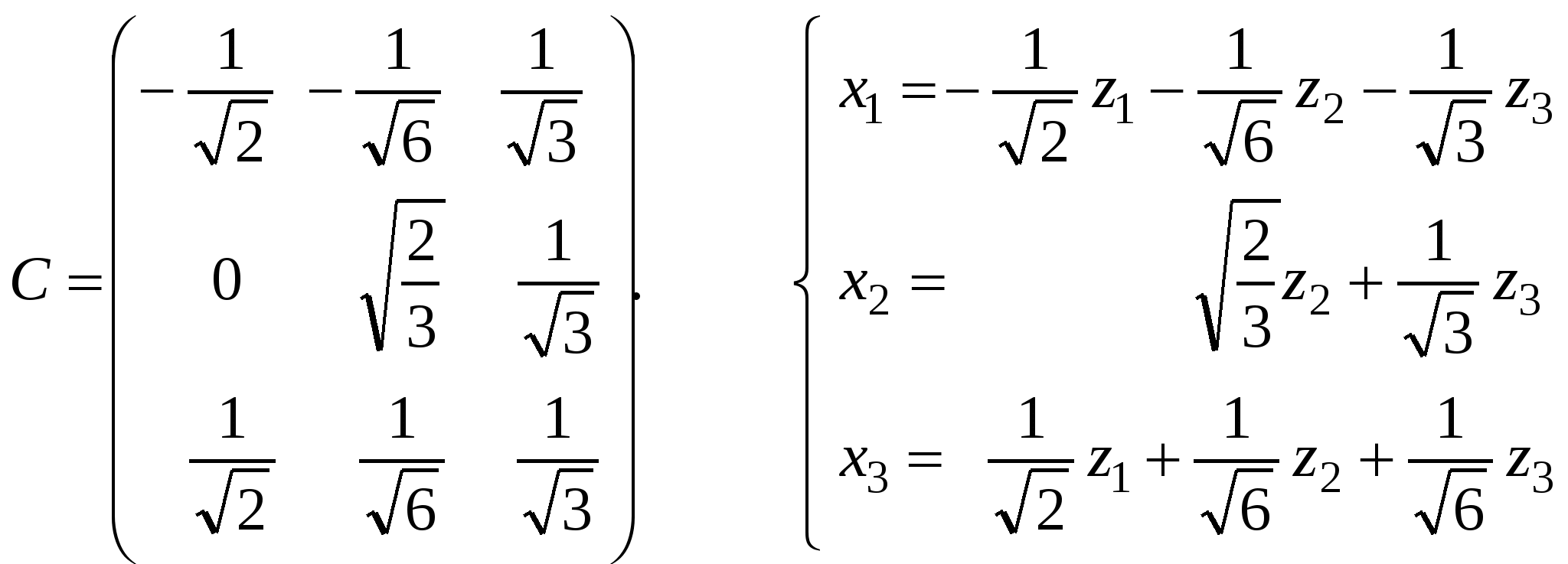 . .
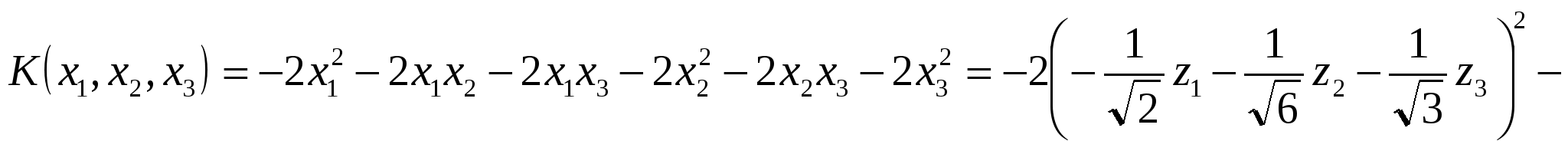
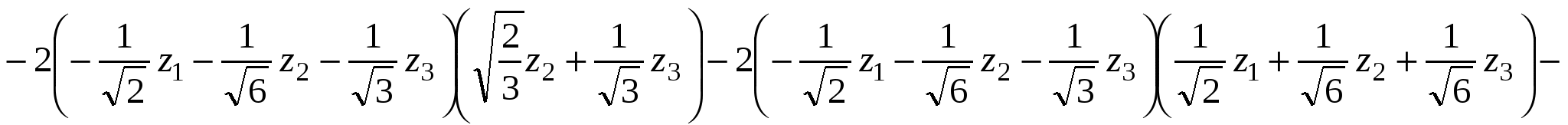
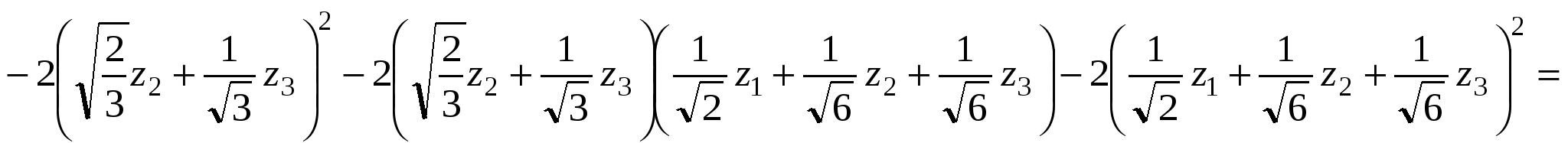
 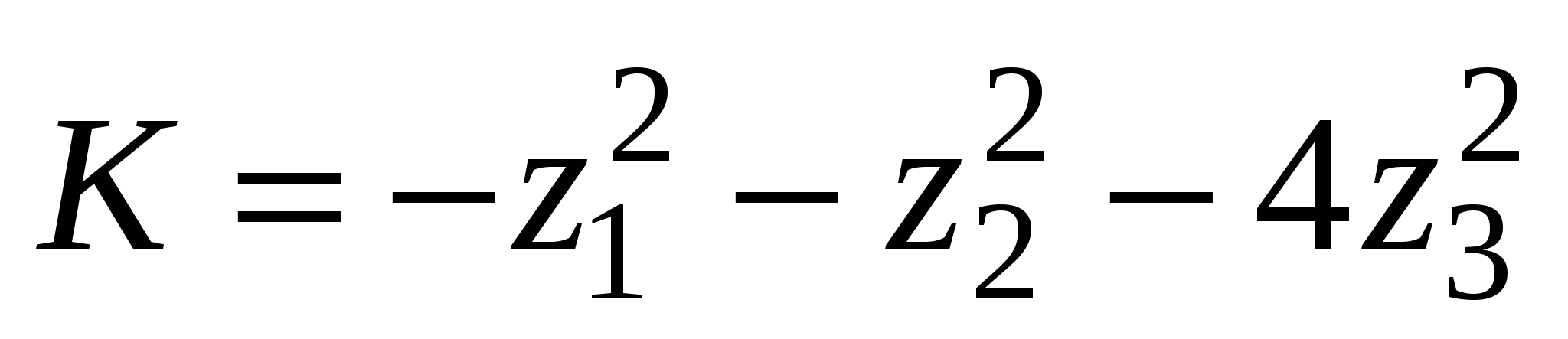 . .
Домашнее задание.
1. Ортогональным преобразованием координат привести квадратичную форму
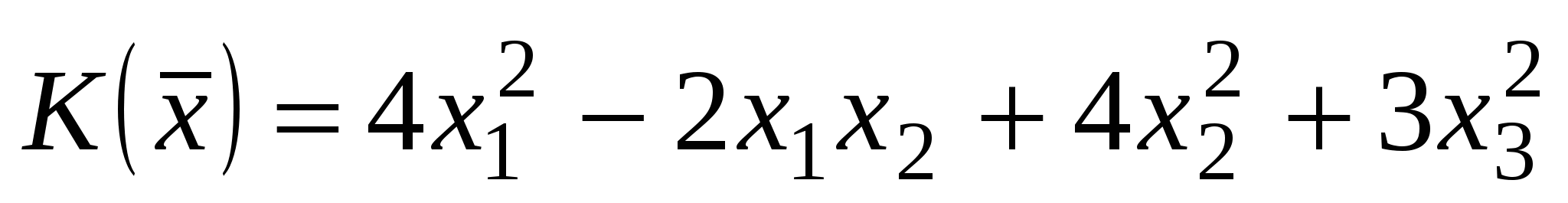 , ,  к каноническому виду. Найти индексы инерции этой формы. к каноническому виду. Найти индексы инерции этой формы. |
|
|
 Скачать 290.5 Kb.
Скачать 290.5 Kb.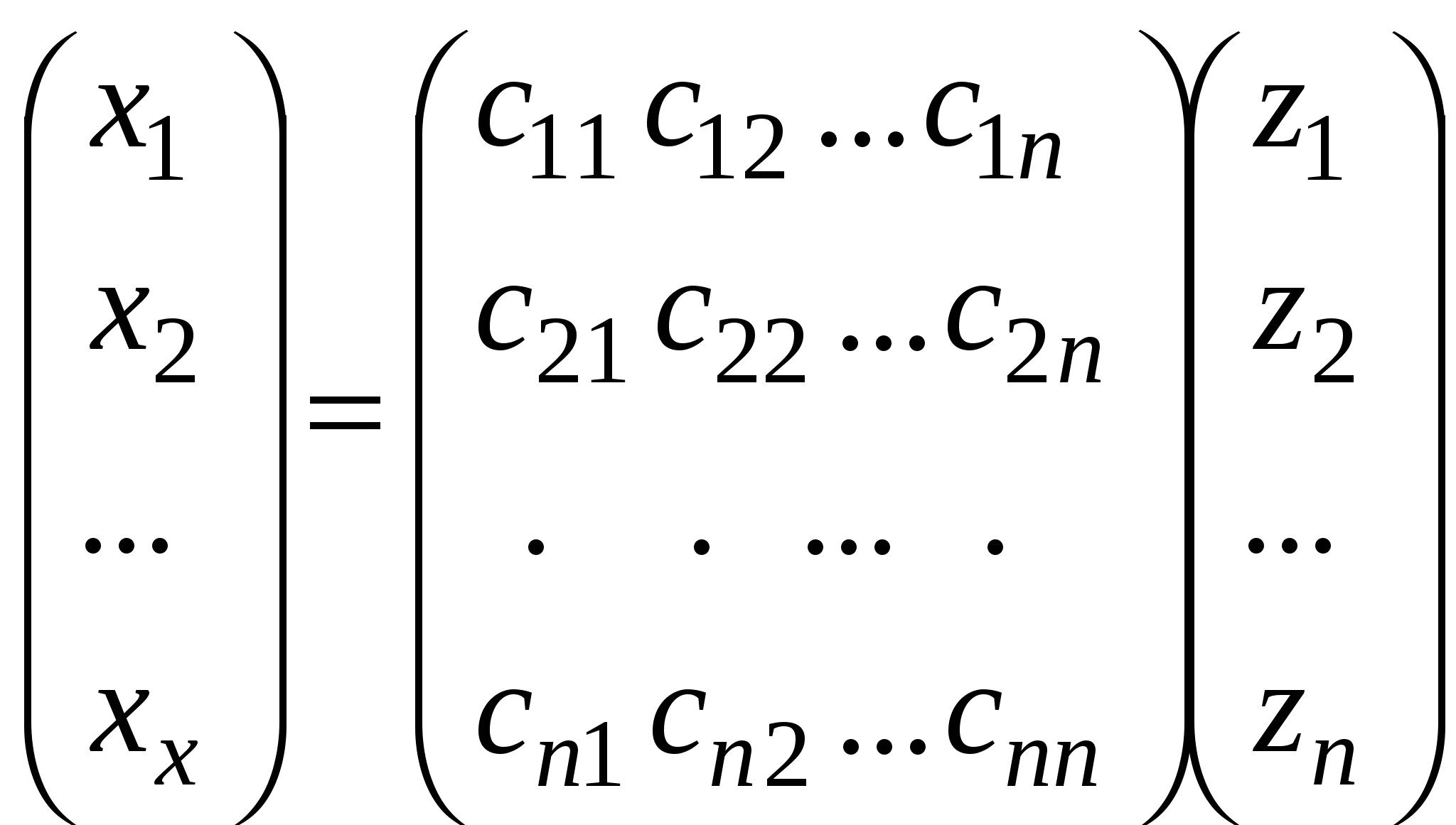 или
или 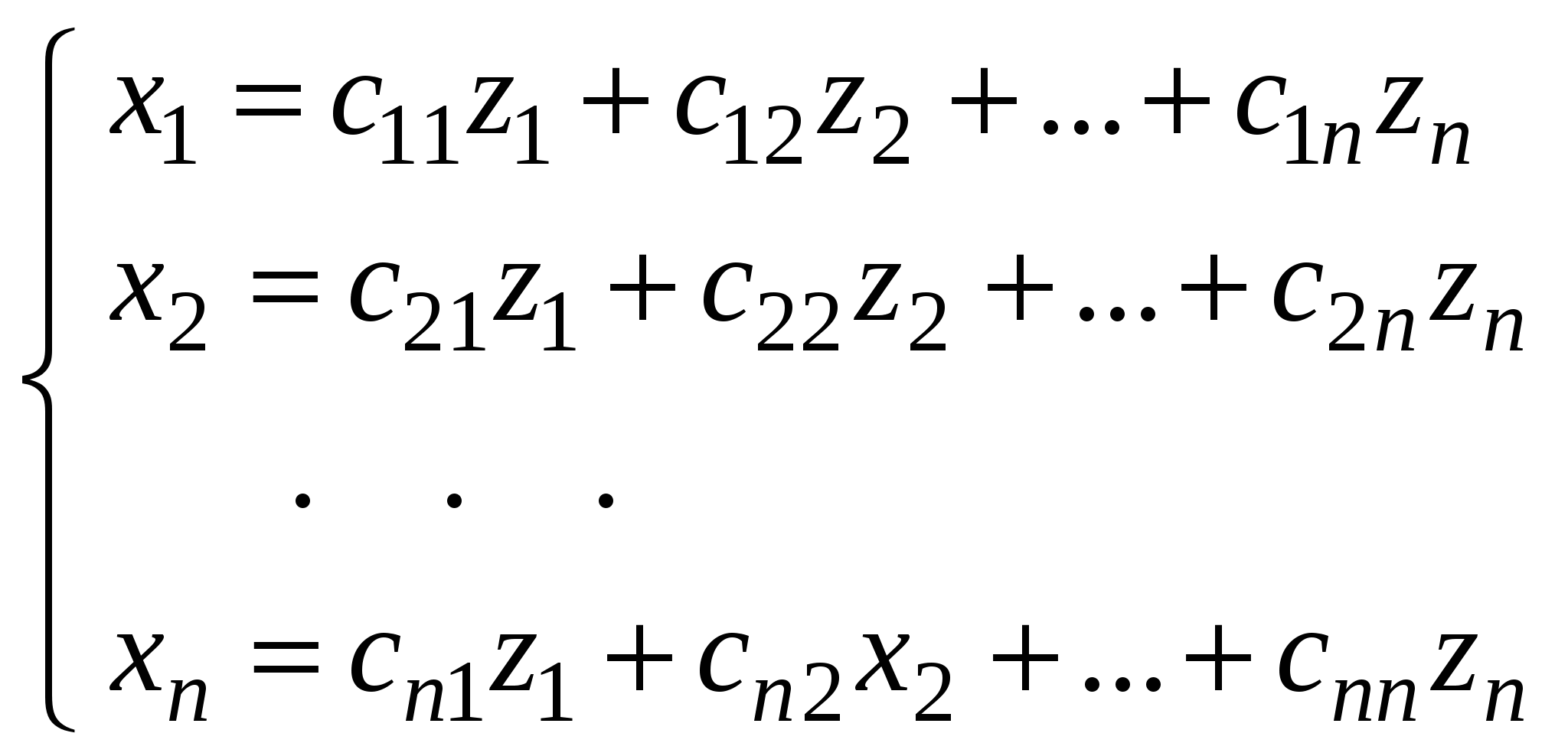 (1)
(1)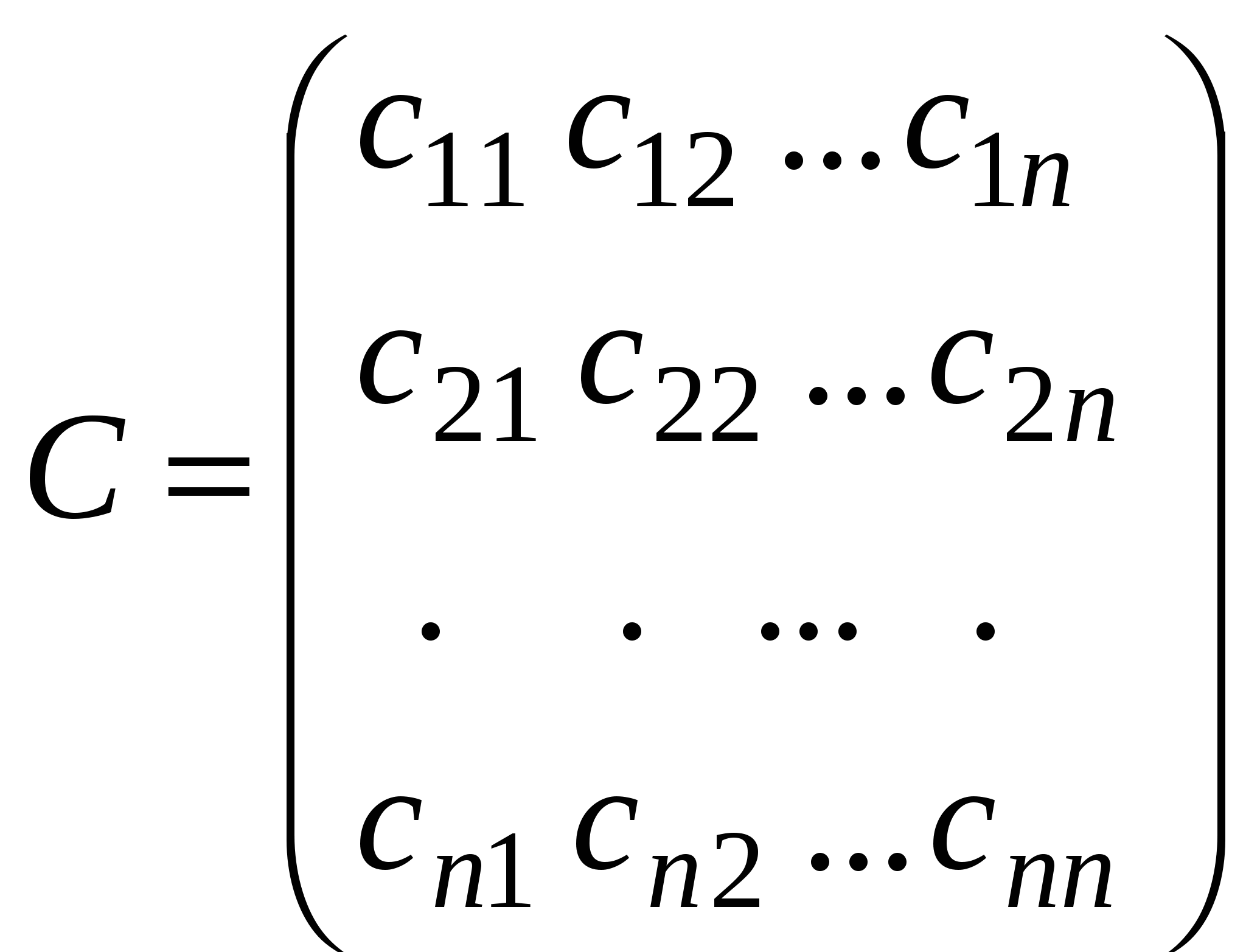 является ортогональной матрицей, т.е.
является ортогональной матрицей, т.е. 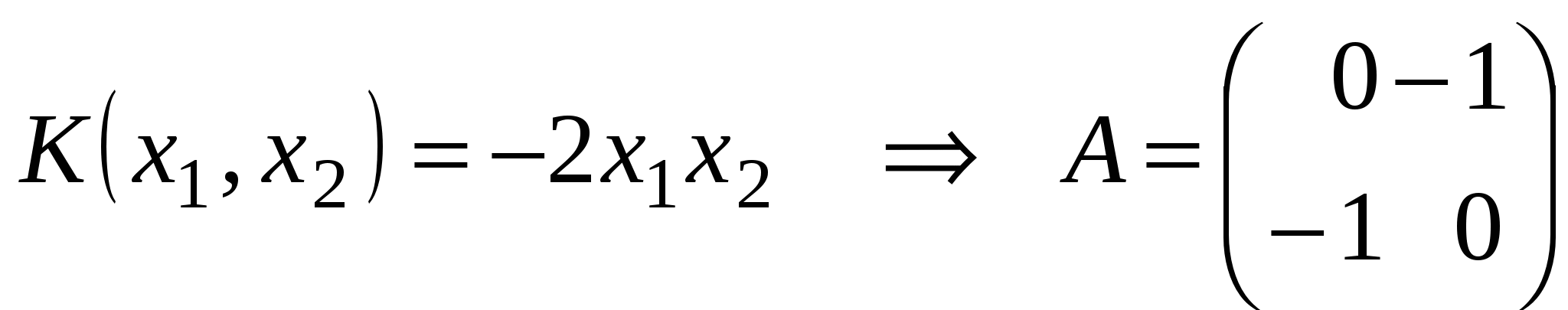 - матрица квадратичной формы. Эту матрицу можно считать матрицей симметричного оператора
- матрица квадратичной формы. Эту матрицу можно считать матрицей симметричного оператора 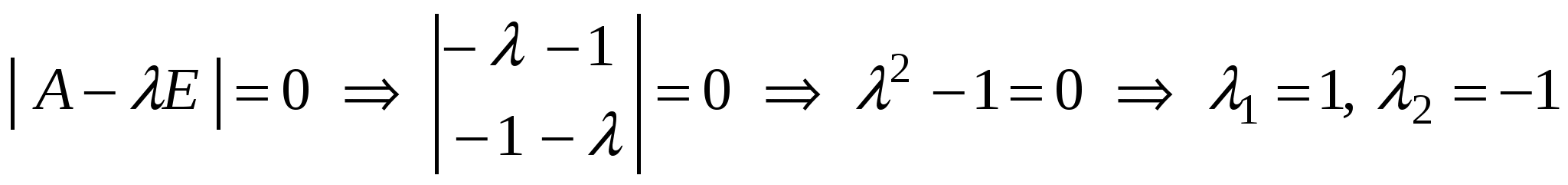 - собственные значения матрицы
- собственные значения матрицы 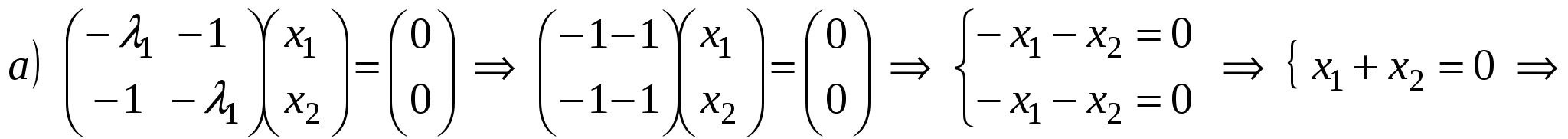
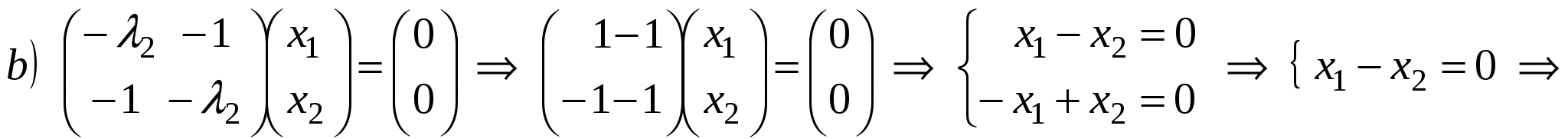
 .
.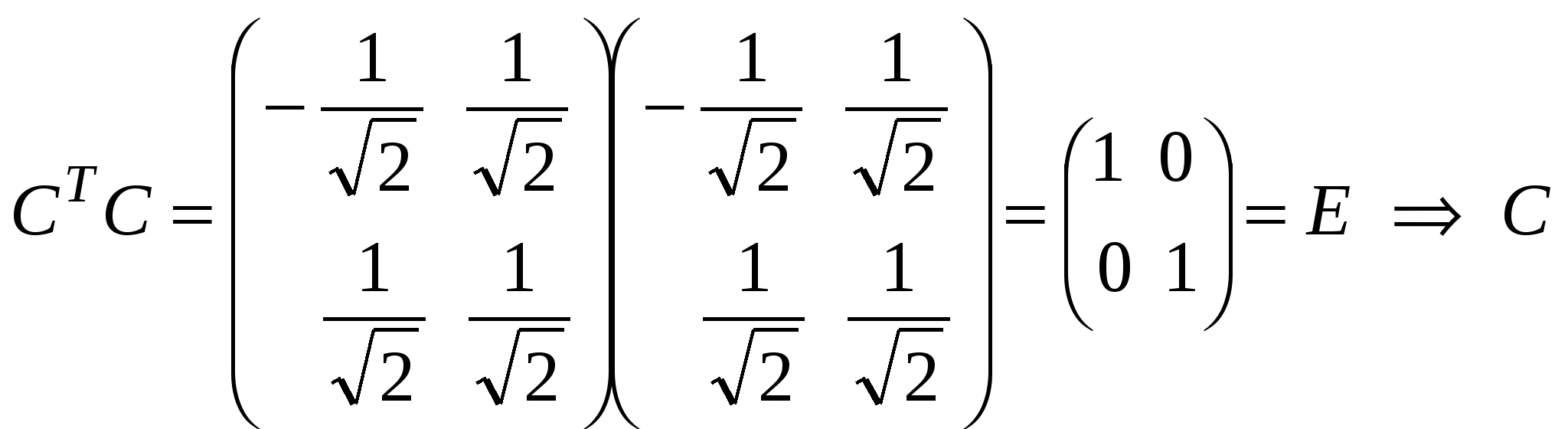 - ортогональная матрица.
- ортогональная матрица.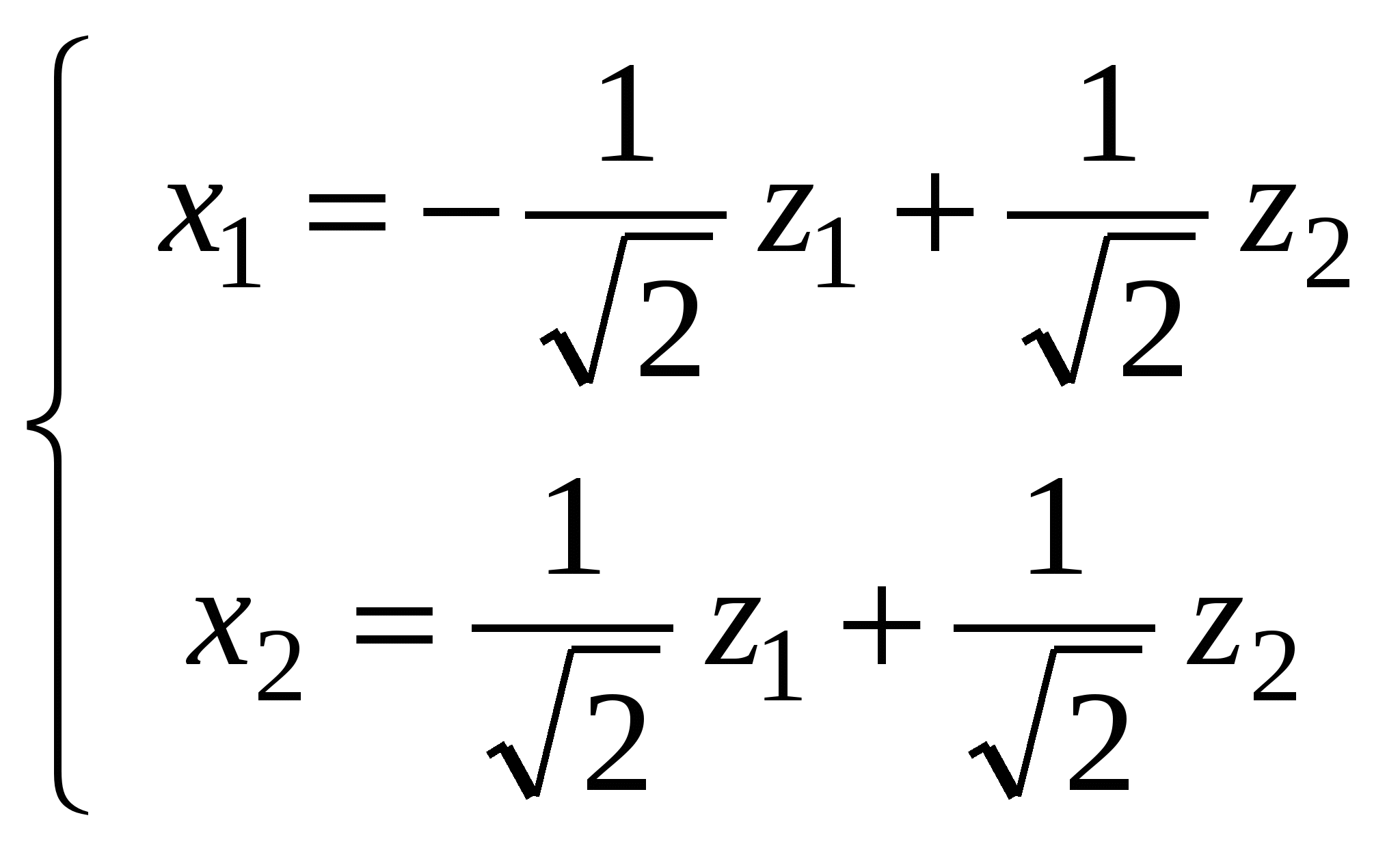 . (3)
. (3) 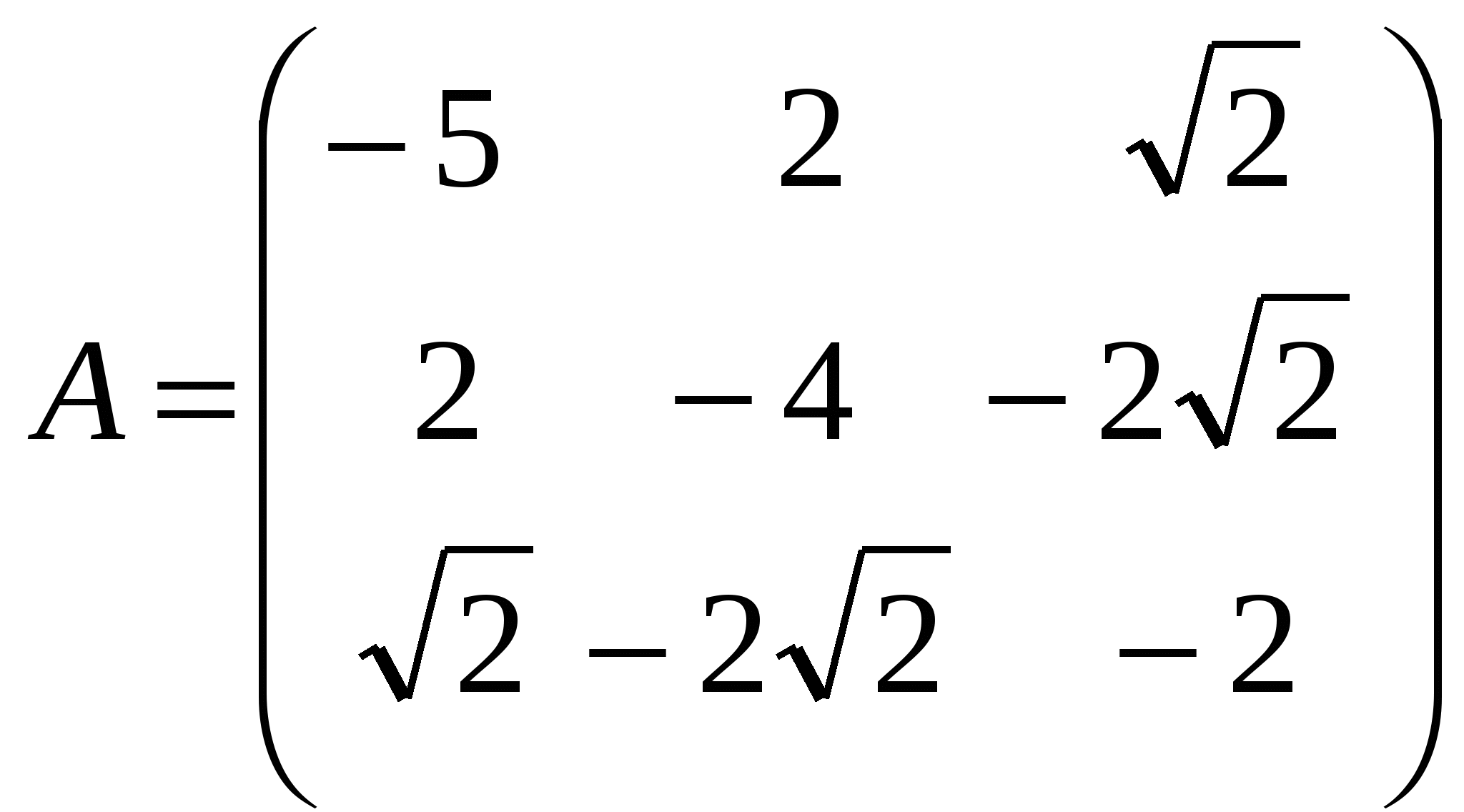 - матрица заданной квадратичной формы.
- матрица заданной квадратичной формы.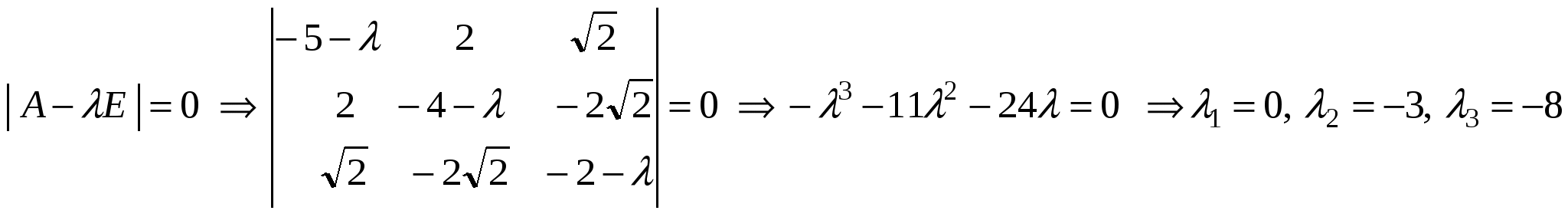 .
.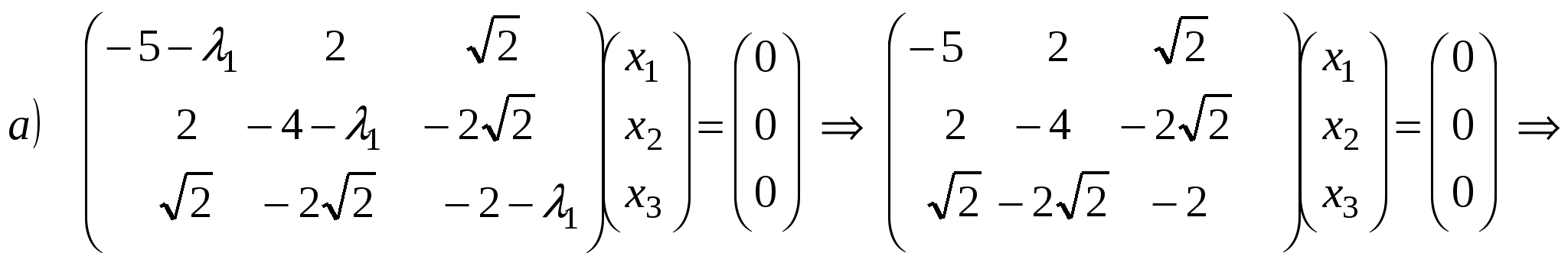
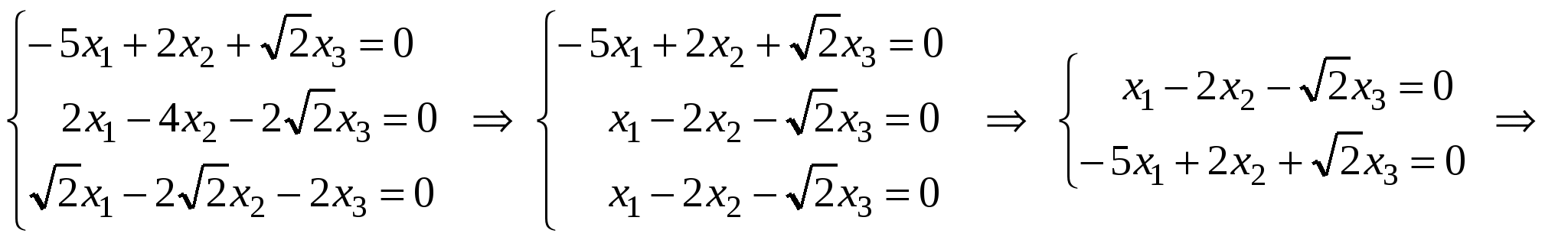


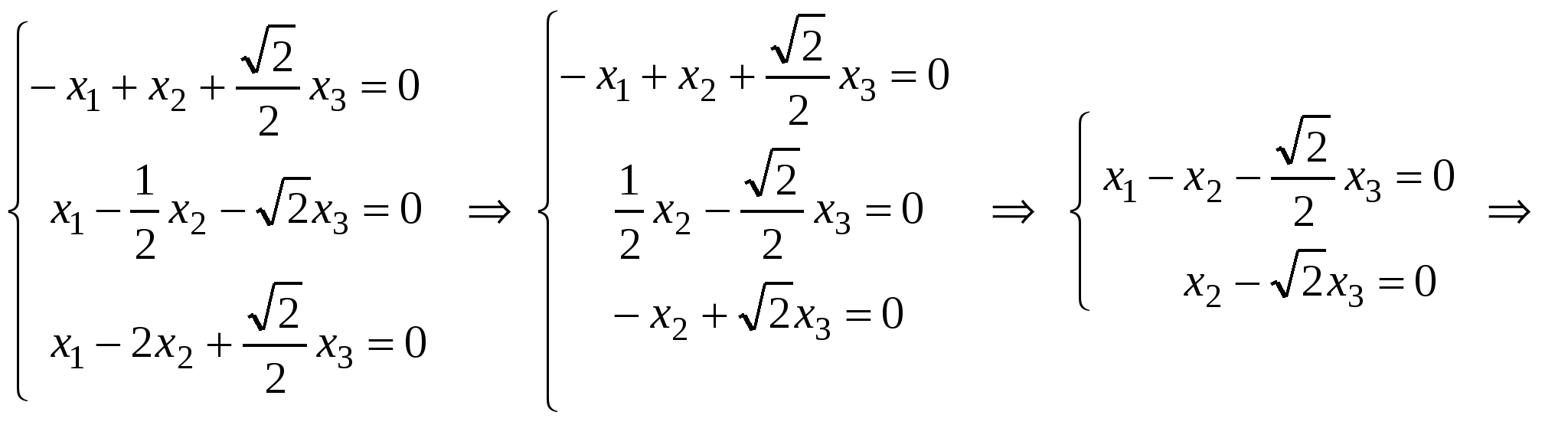
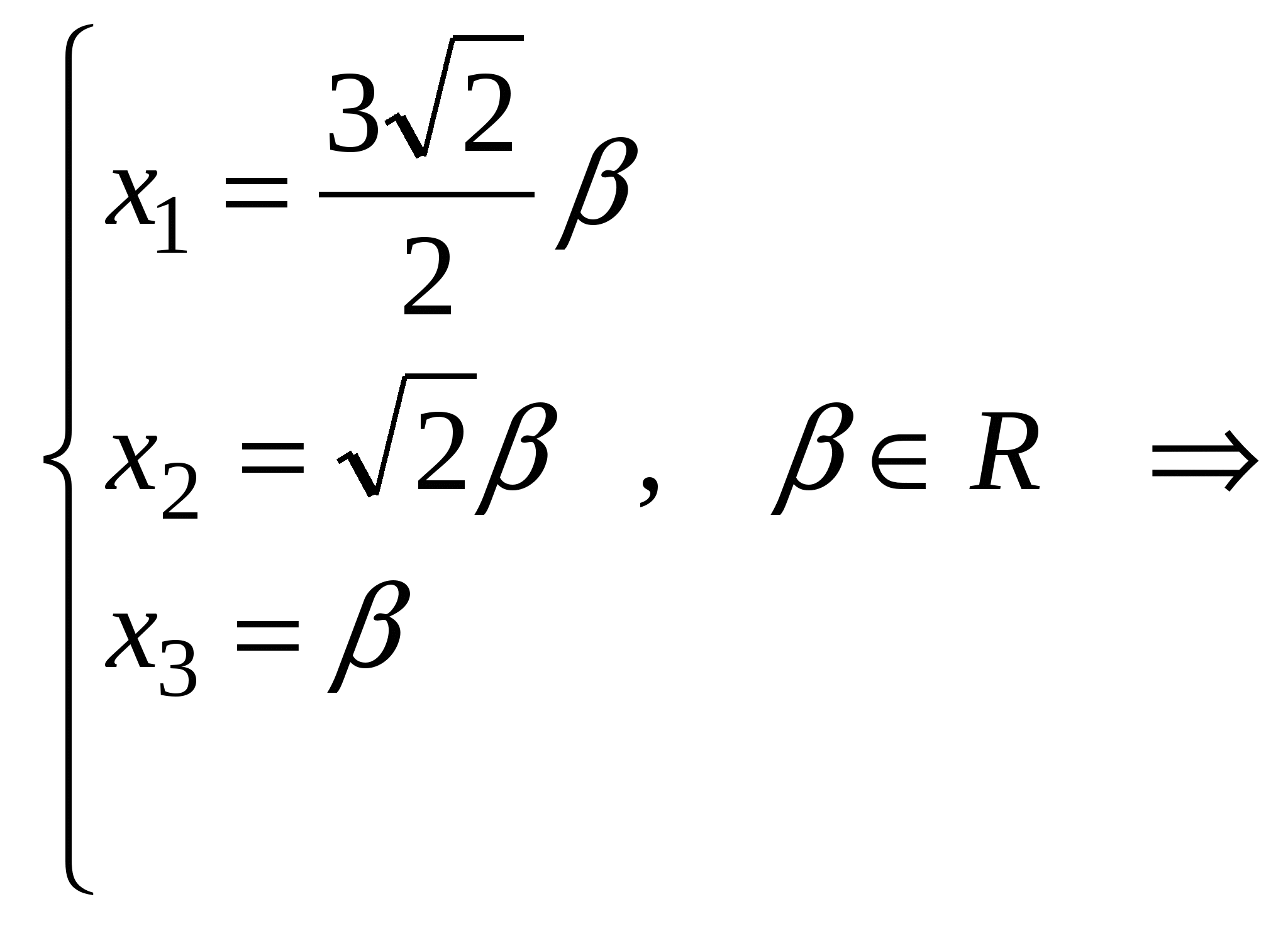
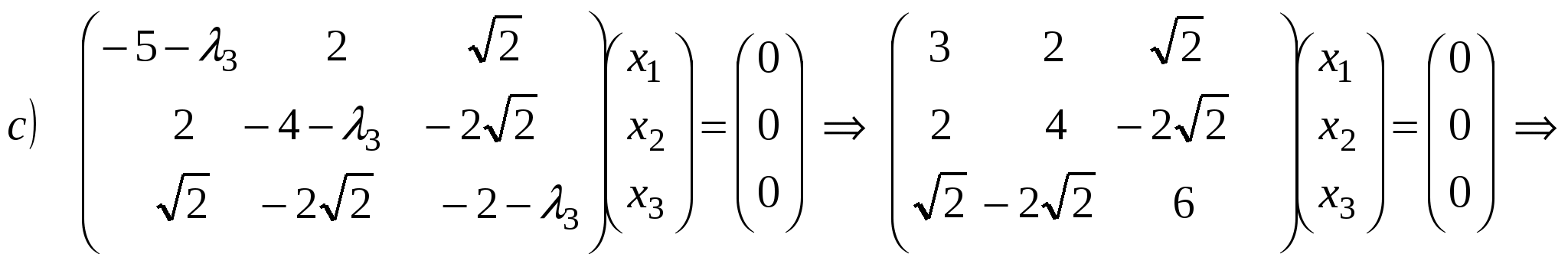
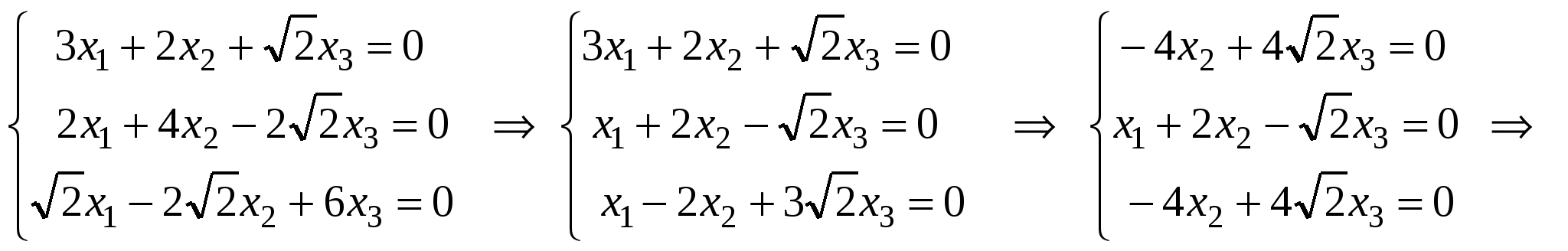

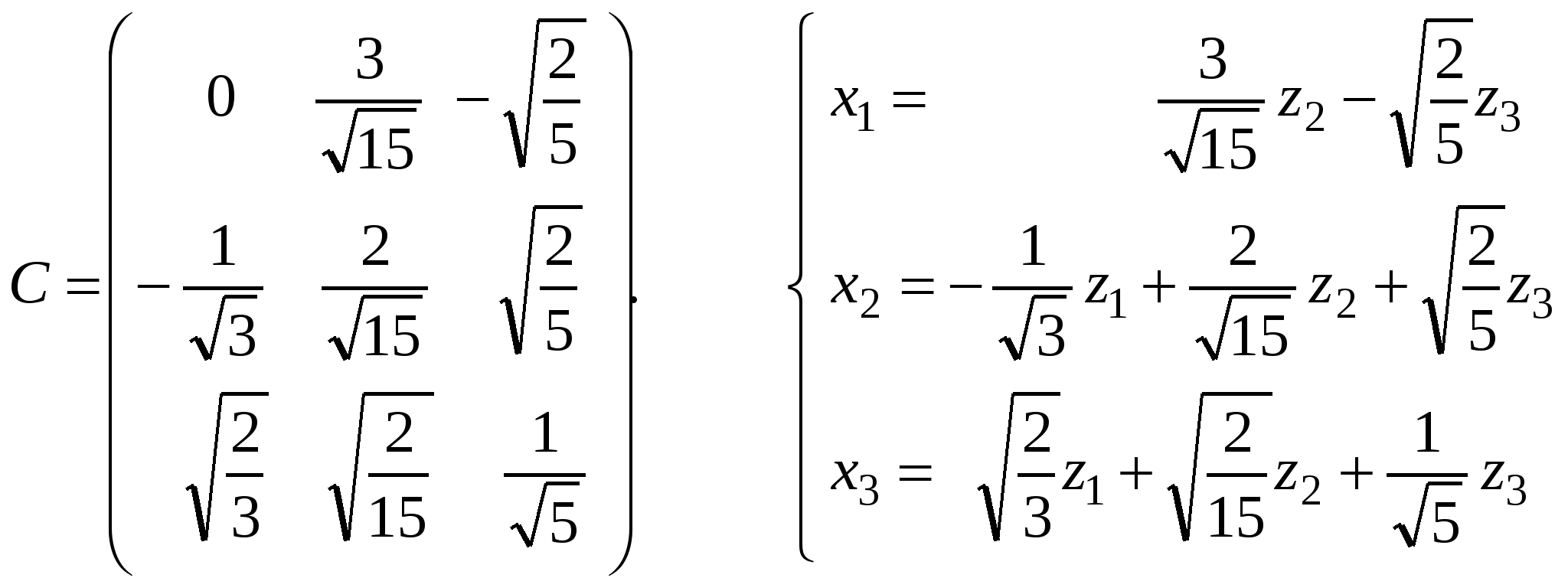 .
.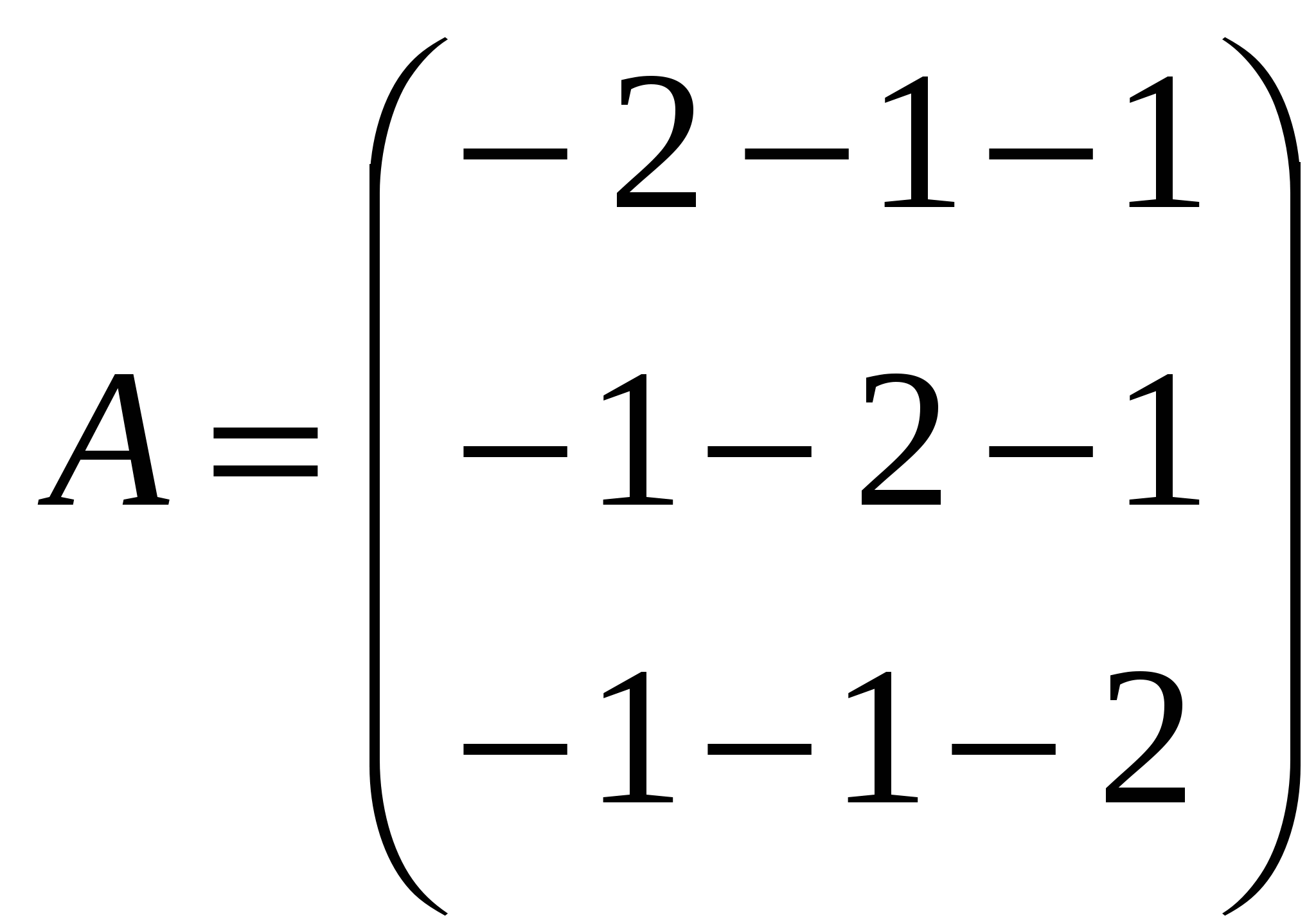 - матрица заданной квадратичной формы. Эту матрицу можно считать матрицей симметричного оператора
- матрица заданной квадратичной формы. Эту матрицу можно считать матрицей симметричного оператора 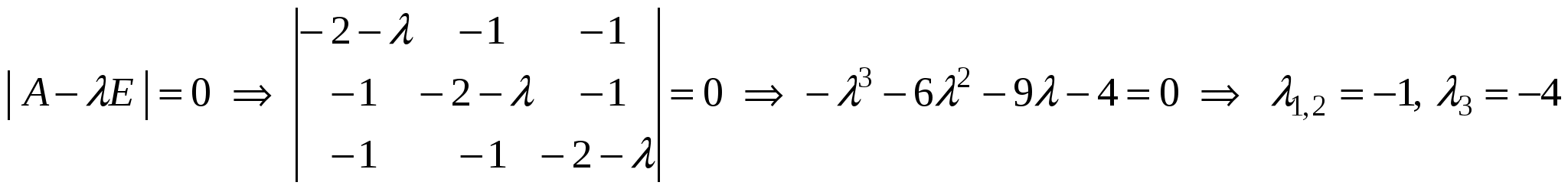 .
.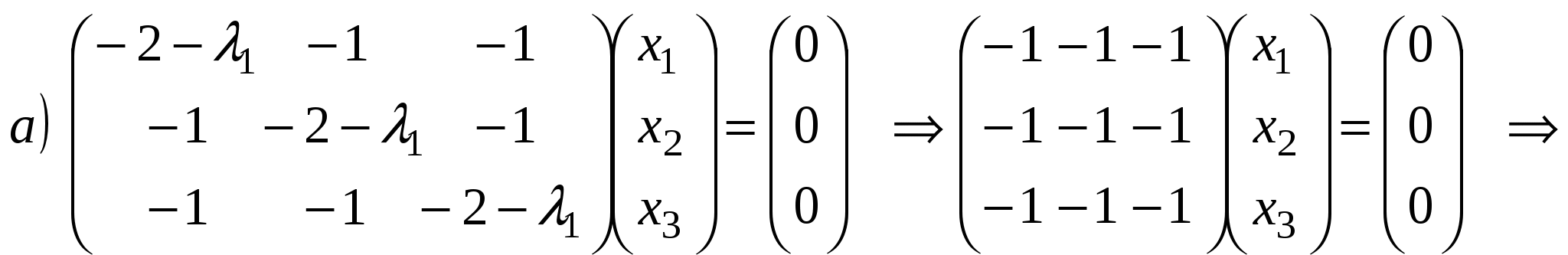

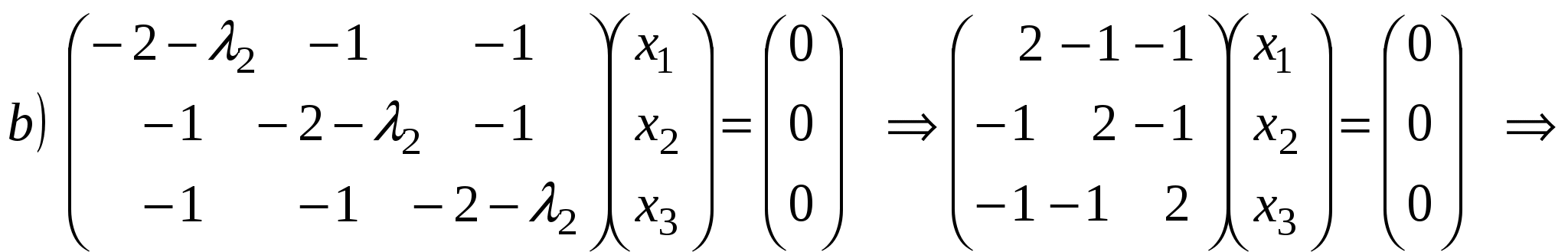

 .
.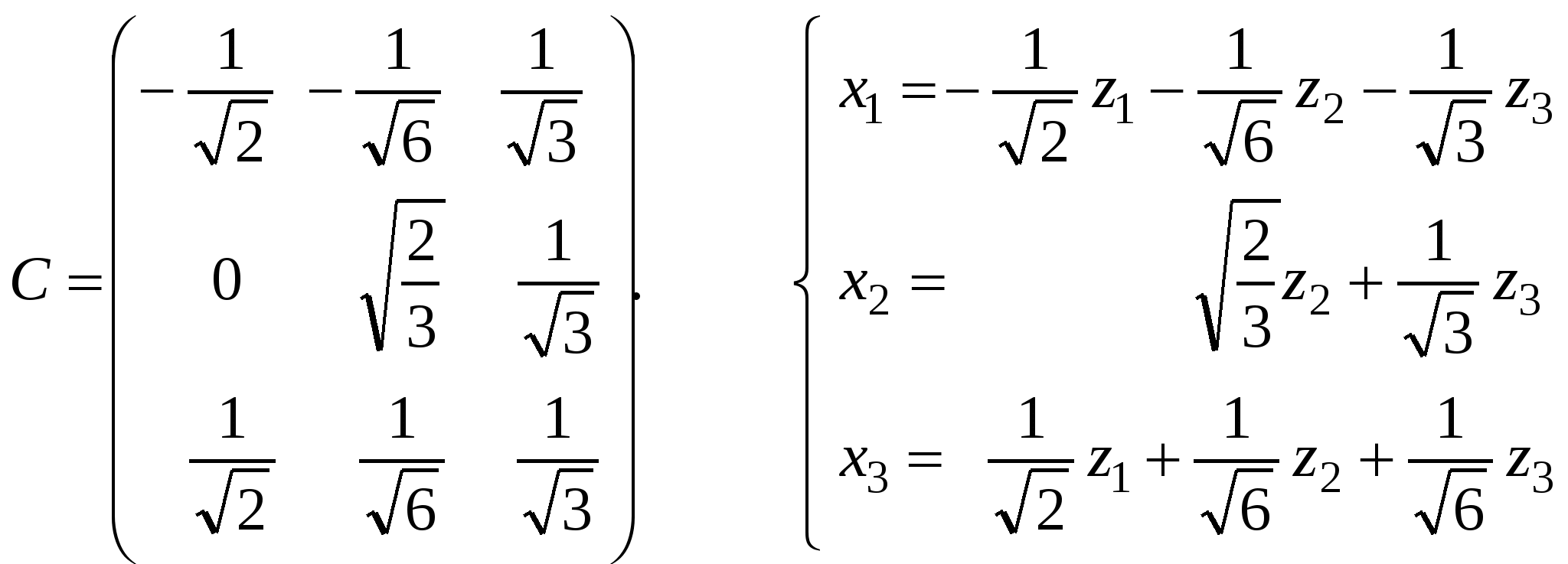 .
.
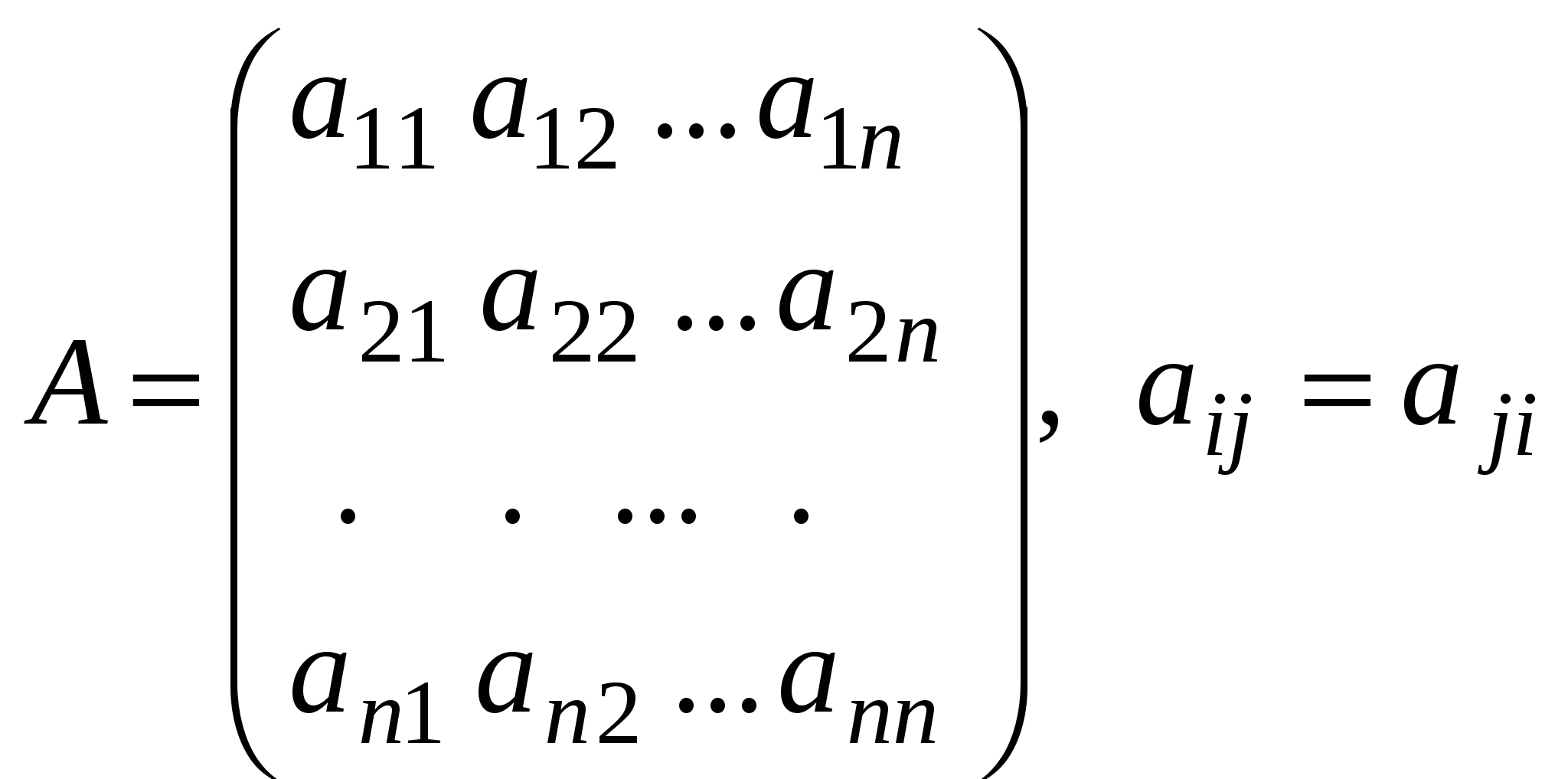 заданной квадратичной формы.
заданной квадратичной формы.