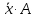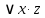Занятие 17. Тема Минимизация функций с помощью карт Карно План лекции Понятие карты Карно
 Скачать 486.76 Kb.
|
|
Занятие 17. Тема «Минимизация функций с помощью карт Карно» План лекции: Понятие карты Карно Виды карт Карно и метод их заполнение Принципы склейки Правило нахождения МДНФ и МКНФ Понятие карты Карно МДНФ – минимальная дизъюнктивная нормальная форма МКНФ - минимальная конъюнктивная нормальная форма Метод карт Карно позволяет быстро получить минимальные ДНФ и КНФ. Карта Карно – это таблица, каждая клетка в ней соответствует набору переменных булевой функции в её таблице истинности. Строки и столбцы карты обозначаются таким образом, чтобы любые соседние клетки по строкам или по столбцам отличались бы между собой значением только одной переменной. Это сделано для того, чтобы было бы возможно применить закон склеивания. Виды карт Карно и метод их заполнение Карта Карно для 2-х переменных – квадратная таблица размером  (4 ячейки)
Ячейки заполняются 0 или 1, полученные в последнем столбце таблицы истинности, соответствующие наборам 00, 01, 10, 11. Карта Карно для 3-х переменных – прямоугольная таблица размером  (8ячеек). Каждая ячейка соответствует наборам 000, 001, 010, 011, 100, 101, 110, 111.
Любые две рядом расположенные клетки являются соседними. Клетки, находящиеся на границах одной строки или столбца, так же считаются соседними, то есть, клетки, которые будут соседними при скручивании карты в вертикальный и горизонтальный цилиндры. 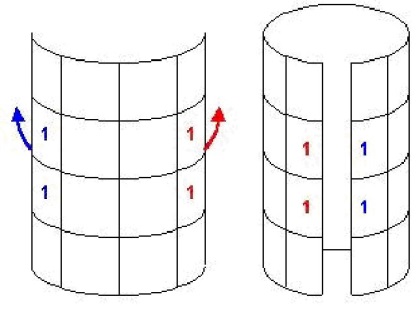  Карта Карно для 4-х переменных – квадратная таблица размером  (16 ячеек). Каждая ячейка соответствует наборам 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111. Карта Карно для 5-х переменных – прямоугольная таблица размером  (32 ячейки). Минимизация функций с помощью карт Карно или нахождение МДНФ (МКНФ) – это процесс склеивания одинаковых значений, стоящих в соседних ячейках. Принципы склейки Склейку клеток карты Карно можно осуществлять по единицам (если необходимо получить МДНФ) или по нулям (если требуется МКНФ). Склеивать можно только прямоугольные области с числом единиц (нулей) 2n, где n — целое число. Область, которая подвергается склейке, должна содержать только единицы (нули). Крайние клетки каждой горизонтали и каждой вертикали также граничат между собой и могут объединяться в прямоугольники. Следствием этого правила является смежность всех четырёх угловых ячеек карты Карно для N=4. Если во всех четырёх угловых ячейках стоят единицы (нули), они могут быть объединены в квадрат. Все единицы (нули) должны попасть в какую-либо область. С точки зрения МДНФ (МКНФ), число областей должно быть как можно меньше (каждая область представляет собой терм), а число клеток в области должно быть как можно больше (чем больше клеток в области, тем меньше переменных содержит терм). Области могут пересекаться. Область должна располагаться симметрично оси (оси располагаются через каждые четыре клетки) Несмежные области, расположенные симметрично оси, могут объединяться в одну. Правило нахождения МДНФ (МКНФ). Берём первую полученную область и смотрим, какие переменные не меняются в пределах этой области, выписываем конъюнкцию для МДНФ (дизъюнкцию для МКНФ) этих переменных; если неменяющаяся переменная нулевая, проставляем над ней инверсию для МДНФ (для МКНФ не ставим инверсию). Если переменная единичная, то не ставим инверсию для МДНФ (ставим инверсию для МКНФ). Берём следующую область, выполняем то же самое, что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией для МДНФ (дизъюнкции областей объединяем конъюнкцию для МКНФ). Функции могут быть записаны не формулой, а аналитическим путем, то есть содержать номера наборов из таблицы истинности дизъюнктивно (  работает с 1) или конъюнктивно (& работает с 0). Например, Y= (1,4,8,10,12,14,15). Это означает, что карта Карно из 4-х переменных заполняется единицами в ячейках с номерами 1,4,8,10,12,14,15, а остальные ячейки заполняются нулями.Пример. 
Для нахождения МДНФ - Составим карту для 3-х переменных и заполним ее 1 из последнего столбца таблицы истинности.
- Выделим покрытия по принципам склейки    - Для каждого покрытия составляем элементарную конъюнкцию, зачеркивая столбец с разными значениями и записывая оставшие переменные с инверсией, если все 0 и без инверсии, если все 1. x y z x y z x y z 0 0 0 0 0 1 1 0 1 0 1 0 1 0 1 1 1 1 МДНФ: у= 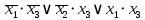 Для нахождения МКНФ - Составим карту для 3-х переменных и заполним ее 0 из последнего столбца таблицы истинности.
- Выделим покрытия по принципам склейки  - Для каждого покрытия составляем элементарную дизъюнкцию, зачеркивая столбец с разными значениями и записывая оставшие переменные с инверсией, если все 1 и без инверсии, если все 0. x y z x y z 1 0 0 0 1 1 1 1 0 МКНФ: у=  Задание для самостоятельного выполнения составить карту Карно и найти МДНФ и МКНФ для следующих функций а)  б)  Ответить на контрольные вопросы: Что называется картой Карно? Какие разновидности карт Карно есть? Как заполняются карты Карно? Для чего нужны принципы склейки?. Чем отличается правило нахождения МДНФ от правила нахождения МКНФ? Пользуясь этим и теоретическим материалом учебника М.С. Спирина «Дискретная математика» глава 4 п.4,6,3 стр.180, выполнить 1 задание. Выполненное задание отправить на адрес электронной почты преподавателя. Имя файла – фамилия студента и номер занятия. (например Петров-17) |
