Занятие 1подходы к понятию и измерению информации
 Скачать 484.62 Kb. Скачать 484.62 Kb.
|
|
Практическое занятие № 2.1.1ПОДХОДЫ К ПОНЯТИЮ И ИЗМЕРЕНИЮ ИНФОРМАЦИИ Цель: Закрепить теоретические знания о понятии информации, свойствах информации, классификации. Познакомиться с определением количества информации. Познакомить с различными подходами к измерению информации. Познакомить с определением количества информации по формуле Шеннона. Способствовать развитию логического мышления, умения анализировать и обобщать. Оборудование, программное обеспечение, материалы: методические указания к практической работе. Техника безопасности: соблюдается в соответствии с инструкцией по ТБ в кабинете ВТ. Информационная часть Количество информации как мера уменьшения неопределенности знания. (Содержательный подход к определению количества информации) Процесс познания окружающего мира приводит к накоплению информации в форме знаний (фактов, научных теорий и т. д.). Получение новой информации приводит к расширению знаний или, как иногда говорят, к уменьшению неопределенности знания. Если некоторое сообщение приводит к уменьшению неопределенности нашего знания, то можно говорить, что такое сообщение содержит информацию. Например, после сдачи зачета или выполнения контрольной работы вы мучаетесь неопределенностью, вы не знаете, какую оценку получили. Наконец, учитель объявляет результаты, и вы получаете одно из двух информационных сообщений: "зачет" или "незачет", а после контрольной работы одно из четырех информационных сообщений: "2", "3", "4" или "5". Информационное сообщение об оценке за зачет приводит к уменьшению неопределенности вашего знания в два раза, так как получено одно из двух возможных информационных сообщений. Информационное сообщение об оценке за контрольную работу приводит к уменьшению неопределенности вашего знания в четыре раза, так как получено одно из четырех возможных информационных сообщений. Ясно, что чем более неопределенна первоначальная ситуация (чем большее количество информационных сообщений возможно), тем больше мы получим новой информации при получении информационного сообщения (тем в большее количество раз уменьшится неопределенность знания). Количество информации можно рассматривать как меру уменьшения неопределенности знания при получении информационных сообщений. Рассмотренный выше подход к информации как мере уменьшения неопределенности знания позволяет количественно измерять информацию. Существует формула, которая связывает между собой количество возможных информационных сообщений N и количество информации I, которое несет полученное сообщение:
Бит. Для количественного выражения любой величины необходимо сначала определить единицу измерения. Так, для измерения длины в качестве единицы выбран метр, для измерения массы - килограмм и т. д. Аналогично, для определения количества информации необходимо ввести единицу измерения. За единицу количества информации принимается такое количество информации, которое содержится в информационном сообщении, уменьшающем неопределенность знания в два раза. Такая единица названа битом. В компьютере информация кодируется с помощью двоичной знаковой системы, и поэтому в кратных единицах измерения количества информации используется коэффициент 2n Так, кратные байту единицы измерения количества информации вводятся следующим образом: 1 килобайт (Кбайт) = 210 байт = 1024 байт; 1 мегабайт (Мбайт) = 210 Кбайт = 1024 Кбайт; 1 гигабайт (Гбайт) = 210 Мбайт = 1024 Мбайт. Алфавитный подход к определению количества информации При алфавитном подходе к определению количества информации отвлекаются от содержания информации и рассматривают информационное сообщение как последовательность знаков определенной зоны рис. 1.5).
Формула (1.1) связывает между собой количество возможных информационных сообщений N и количество информации I, которое несет полученное сообщение. Тогда в рассматриваемой ситуации N - это количество знаков в алфавите знаковой системы, а I - количество информации, которое несет каждый знак: N = 2I. Чем большее количество знаков содержит алфавит знаковой системы, тем большее количество информации несет один знак. В качестве примера определим количество информации, которое несет буква русского алфавита. В русский алфавит входят 33 буквы, однако на практике часто для передачи сообщений используются только 32 буквы (исключается буква "ё"). С помощью формулы (1.1) определим количество информации, которое несет буква русского алфавита: N = 32 => 32 = 2I => 25 = 2I => I=5 битов. Таким образом, буква русского алфавита несет 5 битов информации (при алфавитном подходе к измерению информации Количество информации в сообщении. Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации. Если знаки несут одинаковое количество информации, то количество информации Ic в сообщении можно подсчитать, умножив количество информации Iз, которое несет один знак, на длину кода (количество знаков в сообщении) К: Ic = Iз K Объемный (алфавитный) подход к измерению информации Информация является предметом нашей деятельности: мы ее храним, передаем, принимаем, обрабатываем. Нам часто необходимо знать, достаточно ли места на носителе, чтобы разместить нужную нам информацию, сколько времени потребуется, чтобы передать информацию по каналу связи и т.п. Величина, которая нас в этих ситуациях интересует, называется объемом информации. В таком случае говорят об объемном подходе к измерению информации. Для обмена информацией с другими людьми человек использует естественные языки (русский, английский, китайский и др.). Наряду с естественными языками были разработаны формальные языки (системы счисления, язык алгебры, языки программирования и др.). Основное отличие формальных языков от естественных состоит в наличии строгих правил грамматики и синтаксиса. Например, системы счисления можно рассматривать как формальные языки, имеющие алфавит (цифры) и позволяющие не только именовать и записывать объекты (числа), но и выполнять над ними арифметические операции по строго определенным правилам. Некоторые языки используют в качестве знаков не буквы и цифры, а другие символы, например химические формулы, ноты, изображения элементов электрических или логических схем, дорожные знаки, точки и тире (код азбуки Морзе и др.). Представление информации может осуществляться с помощью языков, которые являются знаковыми системами. Каждая знаковая система строится на основе определенного алфавита и правил выполнения операций над знаками. При хранении и передаче информации с помощью технических устройств информация рассматривается как последовательность символов – знаков (букв, цифр, кодов цветов точек изображения и т.д.) Набор символов знаковой системы (алфавит) можно рассматривать как различные возможные состояния (события). Тогда, если считать, что появление символов в сообщении равновероятно, по формуле N = 2I где N – это количество знаков в алфавите знаковой системы, можно рассчитать I – количество информации, которое несет каждый символ. Информационная емкость знаков зависит от их количества в алфавите. Так, информационная емкость буквы в русском алфавите, если не использовать букву «ё», составляет: 32 = 2I , т.е. I = 5 битов В латинском алфавите 26 букв. Информационная емкость буквы латинского алфавита также 5 битов. На основании алфавитного подхода можно подсчитать количество информации в сообщении Ic, для этого необходимо умножить количество информации, которое несет один символ I, на количество символов K в сообщении: Ic = I х K Например: в слове «информатика» 11 знаков (К=11), каждый знак в русском алфавите несет информацию 5 битов (I=5), тогда количество информации в слове «информатика» Iс=5х11=55 (битов). Интересно, что сама единица измерения количества информации бит (bit) получила свое название от английского словосочетания BInary digiТ, т.е. двоичная цифра. Чем большее количество знаков содержит алфавит знаковой системы, тем большее количество информации несет один знак. Информация в компьютере представлена в двоичном коде, алфавит которого состоит из двух цифр- 0 и 1. Цифра двоичной системы называется битом (от английских слов binary digit - двоичная цифра). Кодирование - это операция преобразования знаков или групп знаков одной знаковой системы в знаки или группы другой знаковой системы. Двоичное кодирование текстовой информации В основе кодирования текстовой информации лежит кодировка символов вводимых с клавиатуры. Основной принцип кодирования символов - договоренность. Код ASCII (American Standard Code for Information Interchange -Американский стандартный код информационного обмена), принятый для персональных компьютеров. Алфавит, отображаемый в двоичные коды, включает знаки, которые можно набрать на клавиатуре компьютера (в том числе комбинаций различных клавиш). Таких знаков 256. Алгоритм определения количества текстовой информации: 1. Определить кол-во символов. 2. Определить сколько бит используется для кодировки 1 символа. 3. Количество информации = число символов * число разрядов в двоичном коде. Вероятностный подход к измерению количества информации За единицу количества информации принимается такое количество информации, которое содержится в информационном сообщении, уменьшающем неопределенность знания в два раза. Такая единица названа битом. Например, после сдачи зачета или выполнения контрольной работы вы мучаетесь неопределенностью, вы не знаете, какую оценку получили. Наконец, учитель объявляет результаты, и вы получаете одно из двух информационных сообщений: "зачет" или "незачет", а после контрольной работы одно из четырех информационных сообщений: "2", "3", "4" или "5". Информационное сообщение об оценке за зачет приводит к уменьшению неопределенности вашего знания в два раза, так как получено одно из двух возможных информационных сообщений. Информационное сообщение об оценке за контрольную работу приводит к уменьшению неопределенности вашего знания в четыре раза, так как получено одно из четырех возможных информационных сообщений. Существует формула, которая связывает между собой количество возможных информационных сообщений N и количество информации I, которое несет полученное сообщение: N = 2i В 1928 году американский инженер Р.Хартли предложил научный подход к оценке сообщений, предложенная формула имеет вид где N- количество равновероятных событий, количество бит сообщения, что любое из N событий произошло. Иногда формулу Хартли записывают  , где K- величина, показывающая сколько раз произошло интересующее нас событие, n- общее число возможных исходов какого то процесса. , где K- величина, показывающая сколько раз произошло интересующее нас событие, n- общее число возможных исходов какого то процесса. Пример 1. На экзамене вы берете экзаменационный билет, и учитель сообщает, что зрительное информационное сообщение о его номере несет 5 битов информации. Если вы хотите определить количество экзаменационных билетов, то достаточно определить количество возможных информационных сообщений об их номерах по формуле (1): N = 25 = 32. Таким образом, количество экзаменационных билетов равно 32 Пример 2. Наоборот, если известно возможное количество информационных сообщений N, то для определения количества информации, которое несет сообщение, необходимо решить уравнение относительно I. Представьте себе, что вы управляете движением робота и можете задавать направление его движения с помощью информационных сообщений: "север", "северо-восток", "восток", "юго-восток", "юг", "юго-запад", "запад" и "северо-запад" (рис. 1.11). Какое количество информации будет получать робот после каждого сообщения? Всего возможных информационных сообщений 8, поэтому формула (1) принимает вид уравнения относительно I: 8 = 2I. Разложим стоящее в левой части уравнения число 8 на сомножители и представим его в степенной форме: 8 = 2 * 2 * 2 = 23. Наше уравнение: 23 = 2I. Равенство левой и правой частей уравнения справедливо, если равны показатели степени числа 2. Таким образом, I = 3 бита, т. е. количество информации, которое несет роботу каждое информационное сообщение, равно 3 битам. Для равновероятностных событий формулу определения количества информации можно рассчитать 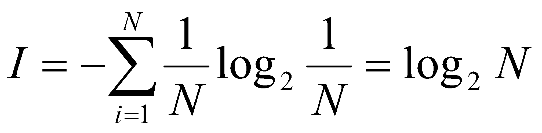 Для разновероятностных событий используется формула Шеннона Алфавитный подход к определению количества информации Определение количества информации на основе уменьшения неопределенности нашего знания рассматривает информацию с точки зрения содержания, ее понятности и новизны для человека. С этой точки зрения в опыте по бросанию монеты одинаковое количество информации содержится и в зрительном образе упавшей монеты, и в коротком сообщении «Орел», и в длинной фразе «Монета упала на поверхность земли той стороной вверх, на которой изображен орел». Однако при хранении и передаче информации с помощью технических устройств целесообразно отвлечься от содержания информации и рассматривать ее как последовательность символов — знаков (букв, цифр, кодов цветов точек изображения и т. д.). Набор символов знаковой системы (алфавит) можно рассматривать как различные возможные состояния (события). Тогда, если считать, что появление символов в сообщении равновероятно, по формуле N=2I можно рассчитать, какое количество информации несет каждый символ. Информационная ёмкость знаков зависит от их количества в алфавите (мощности алфавита): чем больше их количество, тем большее количество информации несет один знак. Так, информационная ёмкость буквы в русском алфавите, если не использовать букву «ё», составляет: 32 = 2I, т. е. I = 5 битов. На основании алфавитного подхода, можно подсчитать количество информации в сообщении, для этого необходимо умножить количество информации, которое несет один символ. ПРАКТИЧЕСКАЯ ЧАСТЬ Задача 1. В велокроссе участвуют 119 спортсменов. Специальное устройство регистрирует прохождение промежуточного финиша каждым из участников, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Каков информационный объем сообщения, записанного устройством после того, как промежуточный финиш прошли 70 велосипедистов?  Решение: так как события равновероятностные для всех участников, то используя формулу находим I=log2119 для записи одного спортсмена. Для решения используем табличный процессор MicrosoftExcel. Выберите Мастер функций, 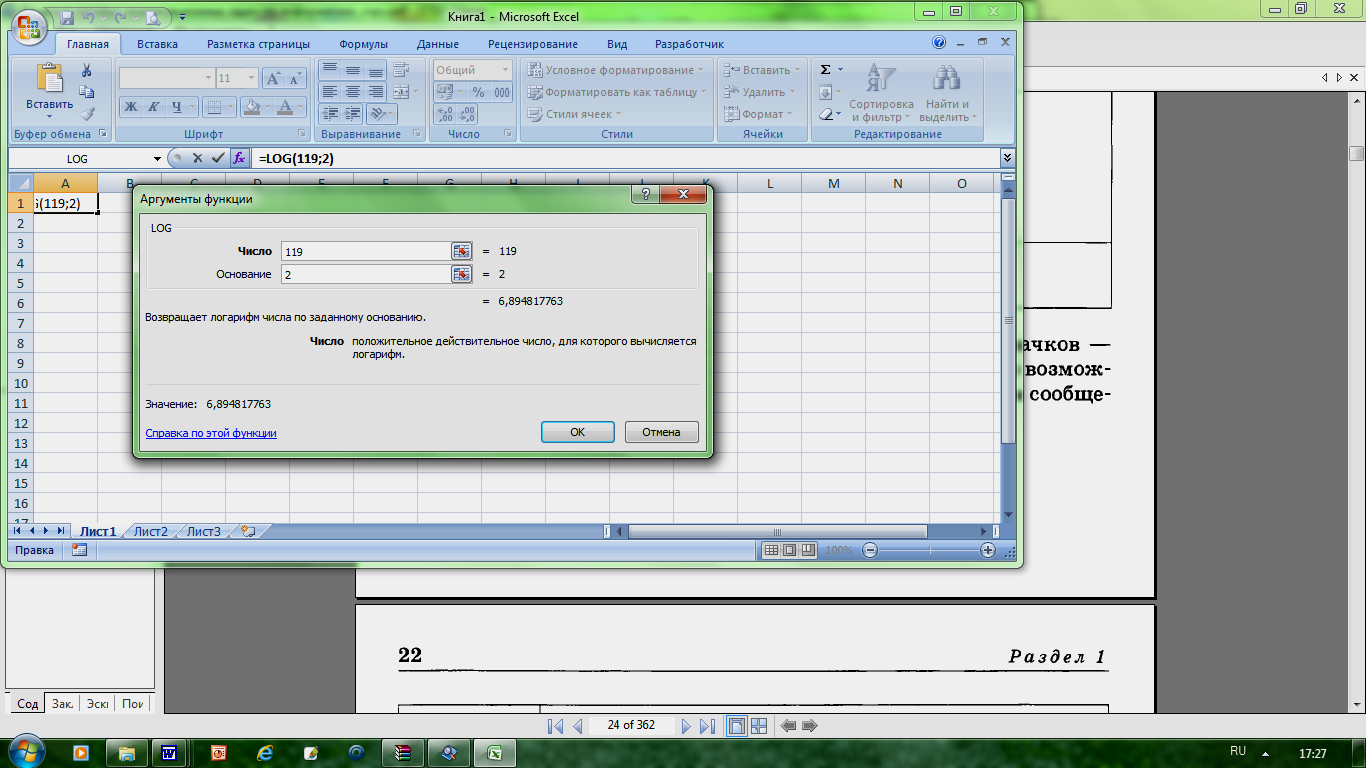 Рисунок 3. Нахождение логарифма Рисунок 3. Нахождение логарифма укажите категорию – математические и найдите функцию логарифма. Введите число участников соревнования в поле- Число. В поле Основание укажите – 2 В ячейке, в которой установлен курсор, появится искомое значение функции. Данное значение будет соответствовать значению количества информации для устройства регистрации одного участника. Умножьте это значение на количество участников. В тетради запишите задачу, решение и ответ. Задание №2. Мощность алфавита равна 256. Сколько Кбайт памяти потребуется для сохранения 160 страниц текста, содержащего в среднем 192 символа на каждой странице? Задание №3. Информационное сообщение объемом 1,5 Кбайта содержит 3072 символа. Сколько символов содержит алфавит, при помощи которого записано это сообщение? Задача №4. Для кодирования нотной записи используется 7 значков — нот. Каждая нота кодируется одним и тем же минимально возможным количеством бит. Чему равен информационный объем сообщения, состоящего из 180 нот? Решение :1) определите какое количество информации необходимо для одной ноты? 2) умножьте значение на количество нот. Задача №5 В корзине лежат 32 клубка шерсти, из них 4 красных. Сколько бит информации несет сообщение о том, что из корзины достали клубок красной шерсти? Решение: Воспользуемся формулой Хартли: log2 (32/4)=log2 (8)=??? Самостоятельно решите следующие задачи: Задание №6. Сколько символов составляет сообщение, записанное с помощью 16-ти символьного алфавита, если объем его составил 1/16 часть Кбайта? Задача №7.У племени "чичевоков" в алфавите 24 буквы и 8 цифр. Знаков препинания и арифметических знаков нет. Какое минимальное количество двоичных разрядов им необходимо для кодирования всех символов? Учтите, что слова надо отделять друг от друга! Задача №8. Книга, набранная с помощью компьютера, содержит 150 страниц. На каждой странице — 40 строк, в каждой строке — 60 символов. Каков объем информации в книге? Ответ дайте в килобайтах и мегабайтах Задача №9. Информационный объем текста книги, набранной на компьютере с использованием кодировки Unicode, — 128 килобайт. Определить количество символов в тексте книги. Задача №10. В корзине лежат 8 черных шаров и 24 белых. Сколько бит информации несет сообщение о том, что из корзины достали черный шар? Задача 11. В коробке лежат 64 цветных карандаша. Сообщение о том, что из коробки достали белый карандаш, несет 4 бит информации. Сколько белых карандашей было в коробке? Задача 12. Бабушка испекла 8 пирожков с капустой, 16 пирожков с повидлом. Маша съела один пирожок. Определить, какое из событий содержит большее количество информации? Решение: 1) Пусть К1 – это количество пирожков с повидлом, К1=24 К2 – количество пирожков с капустой, К2=8 N – общее количество пирожков, N =24+8=32 2) Вычислите вероятность выбора пирожка с разной начинкой и количество информации, которое при этом было получено. Вероятность выбора пирожка с повидлом: р1=К1/N Вероятность выбора пирожка с капустой: р2=? Проверьте себя тем, что в сумме все вероятности дают 1. 3)Вычислите количество информации, содержащееся в сообщении, что Маша выбрала пирожок с повидлом: I1=log2(1/p1) Вычислите количество информации, содержащееся в сообщении, если был выбран пирожок с капустой: I2=log2(1/p2) 4)Сделайте вывод из полученного результата. 5) Определите, как изменяется количество информации с уменьшением вероятности некоторого события? Задача 13. Используя данные задачи 12 сколько получим информации при выборе пирожка любого вида? Решение: Выполните расчет по приведенной формуле. Задача 14. В озере обитает 12500 окуней, 25000 пескарей, а карасей и щук по 6250. Какое количество информации несет сообщение о ловле рыбы каждого вида. Сколько информации мы получим, когда поймаем какую-нибудь рыбу? Решение: Для решения используем MSExcel. Откройте новый лист и создайте следующую таблицу:  Рисунок 4. Таблица в режиме отображения формул Задача №15. В классе 30 человек. За контрольную работу по информатике получено 15 пятерок, 6 четверок, 8 троек и 1 двойка. Какое количество информации несет сообщение о том, что Андреев получил пятерку? Используя подготовленную таблицу для задачи 8, выполните решение задачи. Используя подготовленную таблицу для задачи 8, выполните решение задачи. Задача 16. В некоторой стране автомобильный номер состоит из 7 символов. В качестве символов используют 18 различных букв и десятичные цифры в любом порядке. Каждый номер в компьютерной программе записывается минимально возможным одинаковым целым количеством байт. При этом используют посимвольное кодирование и все символы колируются одинаковым и минимально возможным количеством бит. Определить объем памяти, отводимой в программе для 60 номеров? Контрольные вопросы: Какие подходы к измерению информации рассмотрены вами в ходе выполнения практических заданий? Дайте определение информации. Дайте определение количества информации с точки зрения алфавитного подхода. где используется данный подход Дайте определение количества информации с точки зрения содержательного подхода. где используется данный подход? Что такое мощность алфавита? Объясните на конкретных примерах отличие равновероятного события от неравновероятного? С помощью какой формулы вычисляется вероятность события. Объясните качественную связь между вероятностью события и количеством информации в сообщении об этом событии. В каких случаях применяется формула Шеннона для измерения количества информации. В каком случае количество информации о событии достигает максимального значения. |

