Кодирование. Практическое занятие кодирование информации. Занятие 2 Изучение принципов кодирования чисел
 Скачать 20.49 Kb. Скачать 20.49 Kb.
|
|
Практическое занятие № 2 «Изучение принципов кодирования чисел» Цель работы: изучить способы кодирования чисел в ЭВМ, изучить принципы выполнения арифметических операций с помощью кодов. Образовательные результаты, заявленные в ФГОС: Студент должен уметь: получать информацию о параметрах компьютерной системы; знать: базовые понятия и основные принципы построения архитектур вычислительных систем; организацию и принцип работы основных логических блоков компьютерных систем. Краткие теоретические и учебно-методические материалы по теме практической работы В ЭВМ числа представляются в виде кодов. Различают четыре кода: прямой, обратный, дополнительный и двоично-десятичный. Прямой код При записи числа в прямом коде старший разряд является знаковым разрядом. Если его значение равно 0 – то число положительное, если 1 – то отрицательное. В остальных разрядах (которые называются цифровыми разрядами) записывается двоичное представление модуля числа. Таблица 2.1 –Пример записи чисел в прямом коде
Знаковый разряд в прямом коде не имеет разрядного веса. При выполнении арифметических операций это приводит к необходимости отдельной обработки знакового разряда в прямом коде. Поэтому прямой код главным образом используется для записи положительных чисел. Обратный код Обратный n-разрядный двоичный код положительного целого числа состоит из одноразрядного кода знака (двоичной цифры 0), за которым следует n−1-разрядное двоичное представление модуля числа (обратный код положительного числа совпадает с прямым кодом). Обратный n-разрядный двоичный код отрицательного целого числа состоит из одноразрядного кода знака (двоичной цифры 1), за которым следует n−1-разрядное двоичное число, представляющее собой инвертированное n−1-разрядное представление модуля числа. Таблица 2.2 – Пример записи чисел в обратном коде
Обратный код позволяет вычесть одно число из другого, используя только операцию сложения над натуральными числами. Перенос, возникающий из знакового разряда, при использовании обратного кода должен прибавляться в младший разряд суммы. Пример: необходимо выполнить действие 5-4=1. Это соответствует действию 5+(-4). Обратный код числа 5 равен 00000101, обратные код числа -4 равен 11111011. 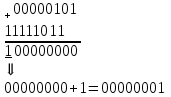 Дополнительный код При записи числа в дополнительном коде старший разряд является знаковым. Если его значение равно 0, то в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом. Если же знаковый разряд равен 1, то в остальных разрядах записано отрицательное двоичное число, преобразованное в дополнительный код. Преобразование числа из прямого кода в дополнительный осуществляется по следующему алгоритму. 1. Если число, записанное в прямом коде, положительное, то к нему дописывается старший (знаковый) разряд, равный 0, и на этом преобразование заканчивается; 2. Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1. Таблица 2.3 – Пример записи чисел в дополнительном коде
Дополнительный код позволяет заменить операцию вычитания операцией сложения, чем упрощает архитектуру ЭВМ. При сложении чисел перенос, возникающий из знакового разряда, не учитывается. Двоично-десятичный код Двоично-десятичный код – форма записи целых чисел, когда каждый десятичный разряд числа записывается в виде его четырёхбитного двоичного кода. Таблица 2.4 – Пример записи числа в двоичном представлении и двоично-десятичном коде
В двоично-десятичном коде существуют запрещённые комбинации битов: 1010, 1011, 1100, 1101, 1110, 1111. Запрещённые комбинации возникают обычно в результате операций сложения, так как в двоично-десятичном коде используются только 10 возможных комбинаций 4-х битового поля вместо 16. Поэтому, при сложении и вычитании чисел формата двоично-десятичного кода действуют следующие правила: - при сложении двоично-десятичных чисел каждый раз, когда происходит перенос бита в старший полубайт, необходимо к полубайту, от которого произошёл перенос, добавить корректирующее значение 0110. - при сложении двоично-десятичных чисел каждый раз, когда встречается недопустимая для полубайта комбинация, необходимо к каждой недопустимой комбинации добавить корректирующее значение 0110 с разрешением переноса в старшие полубайты. - при вычитании двоично-десятичных чисел, для каждого полубайта, получившего заём из старшего полубайта, необходимо провести коррекцию, отняв значение 0110. Пример: переведем числа 25 и 26 в двоично-десятичный код и выполним операцию сложения. 25 в двоично-десятичном коде равно 00100101. 26 в двоично-десятичном коде равно 00100110. 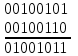 В последнем полубайте получилась запрещенная комбинация битов, поэтому добавляем к нему 0110. 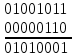 Переведем полученное число из двоично-десятичного кода в десятичный, получим значение 51. 51=25+26 (верно). Задания для практической работы 1 Перевести А и В (таблица 2.5) из десятичной системы в 8-разрядные прямой, обратный и дополнительный коды. 2 Перевести числа С и D (таблица 2.5) из десятичной системы двоично-десятичный код. 3 Выполнить сложение чисел А и В в прямом, обратном и дополнительном коде. Проверить правильность выполнения переводом ответа в десятичное представление. 4 Выполнить сложение чисел С и D в двоично-десятичном коде. Проверить правильность выполнения переводом ответа в десятичное представление. Таблица 2.5 – Таблица вариантов
Контрольные вопросы 1 Для представления каких чисел чаще всего используется прямой код? Назовите недостатки прямого кода 2 Как осуществить перевод чисел в обратный код? 3 Как выполняется операция вычитания в обратном коде? 4 Как осуществить перевод отрицательного числа в дополнительный код? 5 Каковы достоинства и недостатки дополнительного кода? 6 Что собой представляет двоично-десятичный код числа? 7 По какой причине в двоично-десятичном коде существуют запрещенные комбинации битов? |
