выбор типов долот. Занятие 2 Выбор рациональных типов долот
 Скачать 113.23 Kb. Скачать 113.23 Kb.
|
|
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №2 Выбор рациональных типов долот Задача 1. Выбрать тип долота при следующих условиях. Данное стратиграфическое подразделение разбуривалось долотами двух типов. Способ бурения всех скважин турбинный. Параметры режима на данной площади практически одинаковые. Результаты бурения данного стратиграфического подразделения следующие (суммарные по всем скважинам): а) общее число израсходованных долот 1-го типа п1 =12, 2-го типа п2 =22; б) пробурено долотами 1-го типа Н1 =314 м, 2-го типа Н2 =300 м; в) общее время бурения долотами 1-го типа Т1 =116,65 ч, 2-го типа Т2 =93,75 ч. Эти суммарные показатели взяты после проверки совокупности проходок на наличие дефектных данных и исключения их. Решение.Определяем средние показатели но одно долото. Проходка на долото: 1-го типа 2-го типа Стойкость долота: 1-го типа h1 H1 / n1 314 /12 256,2 м; h2 H2 / n2 300 / 22 13,64 м. 2-го типа t2 (T1 / H2 )h1 (116,65 / 314)26,2 9,73 ч; t2 (T2 / H2 )h2 (93,75 / 300)13,64 4,26 ч. Механическая скорость бурения долотом го типа го типа vмех1 H1 / T1 314 /116,65 2,69 м/ч; vмех2 H2 / T2 300 / 93,75 3,2 м/ч. В связи с тем, что h1 > h2 ; t1 > t2 ; а vмех1 < vмех 2 , определяем эксплуатационные затраты на 1 м проходки в рассматриваемых условиях. Дополнительные данные: цена долот 1-го и 2-го типов одинакова и составляет СД = 190 руб. Продолжительность спуско-подъемных операций (нормативная) для данного интервала глубин, отнесена к рейсу долота, с учетом вспомогательных операций составляет tспо tвсп 7 ч. Стоимость 1 ч работы буровой установки по затратам, зависящим от времени ее работы, составляет СВ 29 руб./ч. Определяем величину эксплуатационных затрат на 1 м проходки долотом по формуле где СВ С СВ(t tспо tвсп) СД , h - стоимость 1 ч работы буровой установки по затратам, зависящим от времени; t – стойкость долота; t спо - продолжительность спуско-подъемных операций; tвсп - продолжительность вспомогательных работ; СД - стоимость долота; h – проходка на долото. Подставляя данные в формулу (1), получаем для долота 1-го типа для долота 2-го типа С 29(9,73 7) 190 25,77 руб.; 1 26,2 С 29(4,26 7) 190 37,87 руб. 2 13,64 Так как С1 < С2 (25,77 <37,87), то для разбуривания данного стратиграфического подразделения принимаем долота 1-го типа. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3 ОПРЕДЕЛЕНИЕ НЕОБХОДИМОГО ЧИСЛА ДОЛОТ ПРИ ИХ ИСПЫТАНИИРассчитать необходимое число опытных долот для получения достоверных и надежных результатов в процессе их испытания при следующих условиях: в данном стратиграфическом подразделении отработаны семь серийно выпускаемых долот. Проходка на долото составляет 25; 23; 23; 24; 27; 29; 37 м. Решение. Ранжируем величины проходок (от минимальной до максимальной): 23; 23; 24; 25; 27; 29; 37 м. Проверяем не являются ли две минимальные (23; 23 м) или максимальная (37 м) проходки дефектными. Для исключения явно дефектных данных проверяем максимальные и минимальные величины каждой статистической совокупности следующим образом. Для исключения максимального значения величины проходки данного ряда необходимо условие  n hn hn1 k; (1) минимального значения hn h1  n h2 h1 k. (2) hn h1 Для исключения двух максимальных значений величины проходки данного ряда необходимо условие  n hn hn2 k, (3) двух минимальных значений hn h1  n h3 h1 k, (4) hn h1 Для исключения минимального значения члена ряда в предположении, что и минимальное значение дефектное, необходимо условие  n hn hn1 k, (5) hn h2 Для исключения минимального значения члена ряда в предположении, что и максимальное значение дефектное, необходимо условие  n h2 h1 k, (6) hn h2 Значение величин, входящих в эти формулы: h1 -минимальный (первый) член совокупности чисел; h2 , h3 , hn1 , hn- соответственно второй, третий, предпоследний и последний (максимальный) член ряда Величину kn можно определить по табл. 1 при заданной доверительной вероятности , исходя из числа членов данного ряда n. В нашем случае проверяем, не являются ли две минимальные (23; 23 м) или максимальная (37 м) проходки дефектными. Т а б л и ц а 1
По формуле (4) находим h3 h1 = 24 23 0,071. hn h1 37 23 По табл. 18 для n = 7 находим kn 0,661 . Так как 0,071<0,0661, то минимальная величина проходки не является дефектной. По формуле (1) hn hn1 hn h1 37 29 0,571. 37 23 По табл. 18. для n = 6 находим kn 0,736 . Так как 0,167<0,736, то минимальные значения величины проходки не являются дефектными. По формуле (1) hn hn1 hn h1 29 27 0,333. 29 23 По табл. 1 дл n = 6 находим kn 0,560 . Так как 0,333<0,560, то максимальная величина проходки нового ряда (29 м) не является дефектной; значит, ряд сохраняется. Определяем среднюю проходку на долото h h 23 23 24 25 27 29 25,2 м. СР n 6 Определяем среднее квадратическое отклонение от средней арифметической величины по формуле s hn h1 , d1 (7) где hn h1 - размах варьирования величин после исключения явно дефектных данных; dn-
2,534 
Определяем выборочный коэффициент вариации по формуле кВ s/ hCP, кВ 2,37 / 25,2 0,094. (8) Задаемся предельно допускаемой относительной погрешностью (для шарошечных долот 0,2 0,4 ); при испытаниях 1 0,2 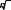 При 2 0,3 определяем величину t / При 2 0,3 определяем величину t /и 2 0,3 . При 1 0,2 t / t / 2 / kB 0,3 / 0,094 3,191. 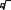 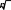 1 / kB 0,2 / 0,094 2,128. 1 / kB 0,2 / 0,094 2,128.По табл. 3 приводится минимальное требуемое число опытных и серийных шарошечных долот сравниваемых конструкций 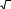 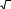 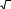 Т а б л и ц а 3 Т а б л и ц а 3
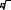 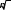 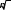 для конкретной характерной пачки пород. Значение величины t / для конкретной характерной пачки пород. Значение величины t /даны при =0,95. По табл. 3 для t / = 3,191 находим n1 5; для t / = 2,128 n2 5 долот. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
