математика. МАТЕМ. Занятие 3 Обучающийся Шаршембай уулу Чынгыз

• Название: Занятие 3 Обучающийся Шаршембай уулу Чынгыз
• Анкор: математика
• Дата: 26.01.2023
• Размер: 159.33 Kb.
• Имя файла: МАТЕМ.odt
• Тип: Занятие; #907437

46.02.01 Документационное обеспечение управления и архивоведение

• 
  
  

Дисциплина: Математика

Практическое занятие 3


Выполнил:

Обучающийся Шаршембай уулу Чынгыз

Преподаватель:

Сазонова Элеонора Борисовна

Вычислите пределы функции, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты):

a)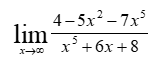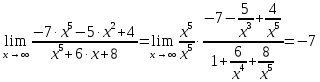





b)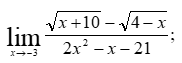  



Для выражения



сопряженным является



Умножим его на числитель и знаменатель.



Учитывая, что (a-b)(a+b) = a2-b2, получаем:



Ответ:

0

 

Задание 2. (Максимальное количество баллов – 2 балла)

Вычислите производные функций, подробно описывая ход решения (указывайте формулы, которыми пользуетесь при решении, записывайте промежуточные результаты):

 

a)  



Решение:



Производную этого выражения находим по формуле: (xn)' = n∙xn-1



(x)' = 1

Здесь:

(-7∙x3)' = -7∙3∙x3-1(x)' = -21∙x2

(x)' = 1





(sin(x))' = cos(x)

Ответ:



При вычислении были использованы следующие правила дифференцирования:

(xa)' = axa-1

(a)' = 0



b)  

Решение:



Здесь:



(3∙x)' = 3

Ответ:



При вычислении были использованы следующие правила дифференцирования:

(xa)' = axa-1

(a)' = 0

(uv)' = u'v + uv'

(f(g(x)))' = f(x)'∙g(x)'

Задание 3. (Максимальное количество баллов - 4 балла)

Вам предложена функция    . Проведите исследование, согласно схеме:

1.   Найти область определения функции.

2.   Найти точки пересечения с осями.

3.   Исследовать функцию на четность/нечетность.

4.   Найти асимптоты.

5.   Найти экстремумы и интервалы монотонности функции.

6.   Найти интервалы выпуклости функции и точки перегиба.

7.   Найти дополнительные точки, уточняющие график.

8.   Построить график.

1) Область определения функции. Точки разрыва функции.

D(y)=R, но х≠±2

2) Четность или нечетность функции.



y(-x) = -y(x), нечетная функция

3) Периодичность функции.

4) Точки пересечения кривой с осями координат.

Пересечение с осью 0Y

x=0, y=0

Пересечение с осью 0X

y=0



x1=0

5) Исследование на экстремум.

y = x^3/(x^2-4)

Найдем точки разрыва функции.

x1 = 2

x2 = -2

Поскольку f(-x)=-f(x), то функция является нечетной.

1. Находим интервалы возрастания и убывания. Первая производная.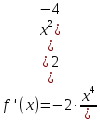



или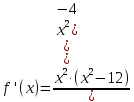



Находим нули функции. Для этого приравниваем производную к нулю

x2∙(x2-12) = 0

Откуда:

x1 = 0

		(-2; 0)	(0; 2)
f '(x) > 0	f '(x) < 0	f '(x) < 0	f '(x) < 0	f '(x) < 0	f '(x) > 0
функция возрастает	функция убывает	функция убывает	функция убывает	функция убывает	функция возрастает

В окрестности точки x = -2∙sqrt(3) производная функции меняет знак с (+) на (-). Следовательно, точка x = -2∙sqrt(3) - точка максимума. В окрестности точки x = 2∙sqrt(3) производная функции меняет знак с (-) на (+). Следовательно, точка x = 2∙sqrt(3) - точка минимума.

2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.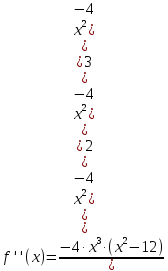



или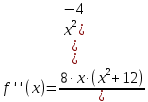



Находим корни уравнения. Для этого полученную функцию приравняем к нулю.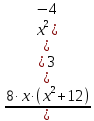



Откуда точки перегиба:

x1 = 0

(-∞ ;-2)	(-2; 0)	(0; 2)	(2; +∞)
f ''(x) < 0	f ''(x) > 0	f ''(x) < 0	f ''(x) > 0
функция выпукла	функция вогнута	функция выпукла	функция вогнута

6) Асимптоты кривой.



Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:



Находим коэффициент k: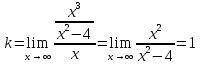





Находим коэффициент b:





Получаем уравнение наклонной асимптоты:

y = x

Найдем вертикальные асимптоты. Для этого определим точки разрыва:

x1 = -2

x2 = 2

Находим переделы в точке x=-2





x1 = -2 - точка разрыва II рода и является вертикальной асимптотой.

Находим переделы в точке x=2





x2 = 2 - точка разрыва II рода и является вертикальной асимптотой.



Найдем наклонную асимптоту при x → -∞:



Находим коэффициент k: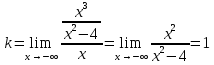





Находим коэффициент b:





Получаем уравнение наклонной асимптоты:

y = x

Вычислите пределы функции, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты):

a)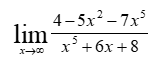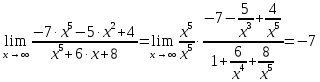





b)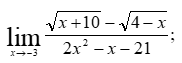  



Для выражения



сопряженным является



Умножим его на числитель и знаменатель.



Учитывая, что (a-b)(a+b) = a2-b2, получаем:



Ответ:

0

 

Задание 2. (Максимальное количество баллов – 2 балла)

Вычислите производные функций, подробно описывая ход решения (указывайте формулы, которыми пользуетесь при решении, записывайте промежуточные результаты):

 

a)  



Решение:



Производную этого выражения находим по формуле: (xn)' = n∙xn-1



(x)' = 1

Здесь:

(-7∙x3)' = -7∙3∙x3-1(x)' = -21∙x2

(x)' = 1





(sin(x))' = cos(x)

Ответ:



При вычислении были использованы следующие правила дифференцирования:

(xa)' = axa-1

(a)' = 0



b)  

Решение:



Здесь:



(3∙x)' = 3

Ответ:



При вычислении были использованы следующие правила дифференцирования:

(xa)' = axa-1

(a)' = 0

(uv)' = u'v + uv'

(f(g(x)))' = f(x)'∙g(x)'

Задание 3. (Максимальное количество баллов - 4 балла)

Вам предложена функция    . Проведите исследование, согласно схеме:

1.   Найти область определения функции.

2.   Найти точки пересечения с осями.

3.   Исследовать функцию на четность/нечетность.

4.   Найти асимптоты.

5.   Найти экстремумы и интервалы монотонности функции.

6.   Найти интервалы выпуклости функции и точки перегиба.

7.   Найти дополнительные точки, уточняющие график.

8.   Построить график.

1) Область определения функции. Точки разрыва функции.

D(y)=R, но х≠±2

2) Четность или нечетность функции.



y(-x) = -y(x), нечетная функция

3) Периодичность функции.

4) Точки пересечения кривой с осями координат.

Пересечение с осью 0Y

x=0, y=0

Пересечение с осью 0X

y=0



x1=0

5) Исследование на экстремум.

y = x^3/(x^2-4)

Найдем точки разрыва функции.

x1 = 2

x2 = -2

Поскольку f(-x)=-f(x), то функция является нечетной.

1. Находим интервалы возрастания и убывания. Первая производная.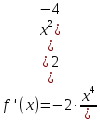



или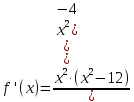



Находим нули функции. Для этого приравниваем производную к нулю

x2∙(x2-12) = 0

Откуда:

x1 = 0

		(-2; 0)	(0; 2)
f '(x) > 0	f '(x) < 0	f '(x) < 0	f '(x) < 0	f '(x) < 0	f '(x) > 0
функция возрастает	функция убывает	функция убывает	функция убывает	функция убывает	функция возрастает

• 
  
  В окрестности точки x = -2∙sqrt(3) производная функции меняет знак с (+) на (-). Следовательно, точка x = -2∙sqrt(3) - точка максимума. В окрестности точки x = 2∙sqrt(3) производная функции меняет знак с (-) на (+). Следовательно, точка x = 2∙sqrt(3) - точка минимума.
  
  2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.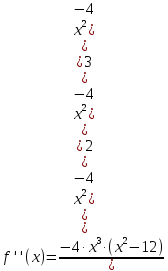
  
  
  
  или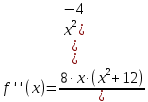
  
  
  
  Находим корни уравнения. Для этого полученную функцию приравняем к нулю.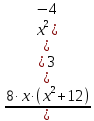
  
  
  
  Откуда точки перегиба:
  
  x1 = 0
  

(-∞ ;-2)	(-2; 0)	(0; 2)	(2; +∞)
f ''(x) < 0	f ''(x) > 0	f ''(x) < 0	f ''(x) > 0
функция выпукла	функция вогнута	функция выпукла	функция вогнута

6) Асимптоты кривой.



Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:



Находим коэффициент k: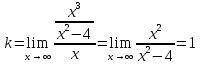





Находим коэффициент b:





Получаем уравнение наклонной асимптоты:

y = x

Найдем вертикальные асимптоты. Для этого определим точки разрыва:

x1 = -2

x2 = 2

Находим переделы в точке x=-2





x1 = -2 - точка разрыва II рода и является вертикальной асимптотой.

Находим переделы в точке x=2





x2 = 2 - точка разрыва II рода и является вертикальной асимптотой.



Найдем наклонную асимптоту при x → -∞:



Находим коэффициент k: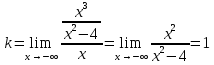





Находим коэффициент b:





Получаем уравнение наклонной асимптоты:

y = x