рдрлрлрлорло. Практическое занятие 6 РЕШЕНИЕ. Занятие 6 самостоятельная работа задача 1 Сколькими способами можно рассадить 5 человек за столом Решение
 Скачать 21.95 Kb. Скачать 21.95 Kb.
|
|
Практическое занятие № 6 САМОСТОЯТЕЛЬНАЯ РАБОТА Задача 1 Сколькими способами можно рассадить 5 человек за столом? Решение В данном случае следует использовать формулу перестановки без повторений: 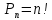 Относительно данного случая (n=5): 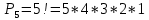 = 120 (способов) = 120 (способов)Ответ: 5 человек за столом можно рассадить 120 различными способами. Задача 2. Сколько четырёхзначных чисел можно составить из четырёх карточек с цифрами 0, 5, 7, 9? Решение Количество возможных перестановок 4 карточек равно: 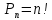 В данном случае n=4: 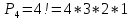 = 24 (способа) = 24 (способа)Однако, в четырехзначном числе на первом месте не может стоять 0, поэтому такие способы следует исключить из общего числа. Число таких исключений равно числу возможных перестановок оставшихся трех цифр: 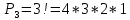 = 6 (способов) = 6 (способов)Таким образом, из данного набора карточек возможно составить 4! – 3! = 24-6 = 18 четырехзначных чисел. Ответ: из четырёх карточек с цифрами 0, 5, 7, 9 можно составить 18 четырёхзначных чисел. Задача 3. В ящике находится 15 деталей. Сколькими способами можно взять 4 детали? Решение Чтобы найти искомое число способов, следует воспользоваться формулой числа сочетаний без повторений:  = = 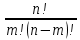 , где: , где:m – выборка n –множество имеющихся элементов То есть в данном случае: 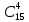 = = 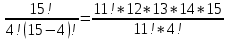 = = 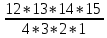 =1365 (способов) =1365 (способов)Ответ: 4 детали из ящика, в котором находится 15 деталей, можно взять 1365 различными способами. Задача 4. Сколькими способами из колоды в 36 карт можно выбрать 3 карты? Решение Чтобы найти искомое число способов, следует воспользоваться формулой числа сочетаний без повторений:  = = 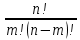 , где: , где:m – выборка n –множество имеющихся элементов То есть в данном случае: 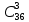 = = 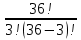 = = 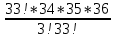 = = 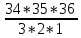 = 7140 (способов) = 7140 (способов)Ответ: из колоды в 36 карт выбрать 3 карты можно 7140 различными способами. Задача 4. В шахматном турнире участвует k человек и каждый с каждым играет по одной партии. Сколько всего партий сыграно в турнире? Решение Чтобы найти искомое число партий, следует воспользоваться формулой числа сочетаний без повторений:  = = 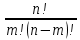 , где: , где:m – выборка n –множество имеющихся элементов В данном случае число m=2, так как в каждой партии играет 2 человека, а множество n = k, поэтому: 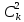 = = 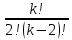 = = 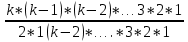 = = 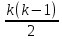 (партий) (партий)Ответ: при участии в турнире k человек всего будет сыграно 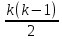 партий. партий.Задача 5. Боря, Дима и Володя сели играть в «очко». Сколькими способами им можно сдать по одной карте? (колода содержит 36 карт) Решение: Для решения необходимо использовать формулу размещения без повторений: 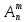 = = 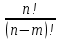 , где: , где:m – выборка n – множество имеющихся элементов В данном случае m = 3, n = 36: 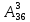 = = 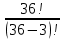 = = 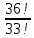 = 36*35*34 = 42840 (способов) = 36*35*34 = 42840 (способов)Ответ: по одной карте сдать можно 42840 различными способами. Задача 6. В студенческой группе 23 человека. Сколькими способами можно выбрать старосту и его заместителя? Решение Для решения необходимо использовать формулу размещения без повторений: 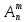 = = 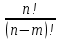 , где: , где:m – выборка n – множество имеющихся элементов В данном случае m = 2, n = 23: 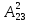 = = 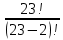 = = 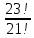 = 23*22 = 506 (способов) = 23*22 = 506 (способов)Ответ: в группе из 23 человек старосту и заместителя можно выбрать 506 различными способами. Задача 7. Студенческая группа состоит из 23 человек, среди которых 10 юношей и 13 девушек. Сколькими способами можно выбрать двух человек одного пола? Решение Данная задача подразумевает, что можно выбрать двух юношей или двух девушек. То есть в данном случае используется сложение комбинаций, а именно возможного выбора 2 юношей из 10 или 2 девушек из 13, значит: 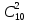 + + 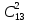 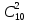 = = 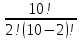 = = 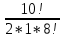 = =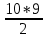 = 45 (способов) = 45 (способов)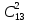 = = 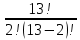 = = 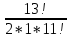 = =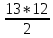 = 78 (способов) = 78 (способов)Общее число способов равно 45+78 = 123 способа. Ответ: двух человек одного пола из 10 юношей и 13 девушек можно выбрать 123 различными способами. Задача 8. Сколько существует трёхзначных чисел, которые делятся на 5? Решение У каждого трехзначного числа есть по одной цифре в разряде сотен, десятков и единиц. В разряде сотен может находится любая цифра кроме 0, так как в таком случае число не будет считаться трехзначным. То есть необходимо выбрать 1 цифру из 9. ( 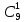 ) )В разряде десятков может стоять любая из 10 цифр от 0 дог 9. То есть необходимо выбрать одну цифру из 10 ( 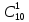 ) )Чтобы число делилось на 5, в разряде единиц должны быть только 0 или 5, то есть 2 цифры. Для построения трехзначного числа, которое делится на 5, необходимо выполнение всех трех вышеперечисленных условий, поэтому необходимо применить умножение комбинаций: 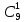 * *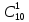 * 2 = 9*10*2 = 180 (чисел) * 2 = 9*10*2 = 180 (чисел)Ответ: всего существует 180 трехзначных чисел, которые делятся на 5. Задача 9. Сколько существует выигрышных комбинаций из 2 карт при игре в «очко»? Решение Выигрышными комбинациями в «очко» следует считать одновременную сдачу 2 тузов или 1 туза и 1 десятки. Так как в колоде карт 4 туза и 4 десятки, то способов сдать 2 туза: 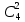 = =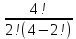 = = 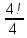 = 6 (комбинации) = 6 (комбинации)А одновременной сдачи десятки и туза: 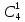 * *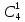 = 4*4 = 16 (комбинации) = 4*4 = 16 (комбинации)Так как обе из рассматриваемых комбинаций выигрышные, то общее число выигрышных комбинаций находится по правилу сложения: 16+6 = 22 (комбинации) Ответ: в игре «очко» 22 выигрышных комбинаций из 2 карт. Задача 10. У Васи дома живут 4 кота. а) сколькими способами можно рассадить котов по углам комнаты? б) сколькими способами можно отпустить гулять котов? в) сколькими способами Вася может взять на руки двух котов (одного на левую, другого – на правую)? Решение а) Используется правило перестановки без повторений: 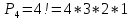 = 24 (способа) = 24 (способа)б) На прогулку котов можно отпустить всех четырех, трех, двух или одного кота. - Способов отпустить гулять одного из четырех котов всего 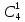 = 4 способа; = 4 способа;- Способов отпустить гулять двух из четырех котов всего 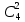 = = 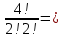 6 способов 6 способов- Способов отпустить гулять трех из четырех котов всего  = = 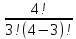 = 4 способа = 4 способа- Один способ отпустить гулять всех четырех котов Так как устраивает любой из перечисленных вариантов, то для общего числа способов следует сложить комбинации: 4+6+4+1 = 15 (способов) в) В данном случае необходимо воспользоваться формулой размещения без повторений, так как учитываются разные руки Васи: 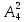 = = 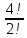 = = 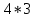 =12 (способов) =12 (способов)Ответ: а) котов по углам комнаты можно рассадить 24 способами; б) котов на прогулку можно отправить 15 способами; в) взять на руки двух котов можно 12 способами. |
