Занятие 8(Фдз 9). Занятие 8 (Фдз 9). Линейные, билинейные и квадратичные функции в линейном пространстве
 Скачать 410 Kb. Скачать 410 Kb.
|
|
Занятие 8 (Фдз 9). Линейные, билинейные и квадратичные функции в линейном пространстве. 8.1. Линейная функция в линейном пространстве и ее представление в заданном базисе. 8.2. Билинейная функция в линейном пространстве и соответствующая ей билинейная форма в заданном базисе. Векторно-матричная запись билинейной формы. Матрица билинейной формы, закон ее изменения при переходе к новому базису и инвариантность ранга этой матрицы. 8.3. Квадратичная функция в линейном пространстве. Симметричные билинейные функции и соответствующие им квадратичные функции. Квадратичные функции и соответствующие им квадратичные формы. Матрица квадратичной формы. 8.1. Пусть или Если Пример 1. На линейном векторном пространстве Решение. Согласно (2) функция Выполнены оба свойства (2). Следовательно, Пример 2. 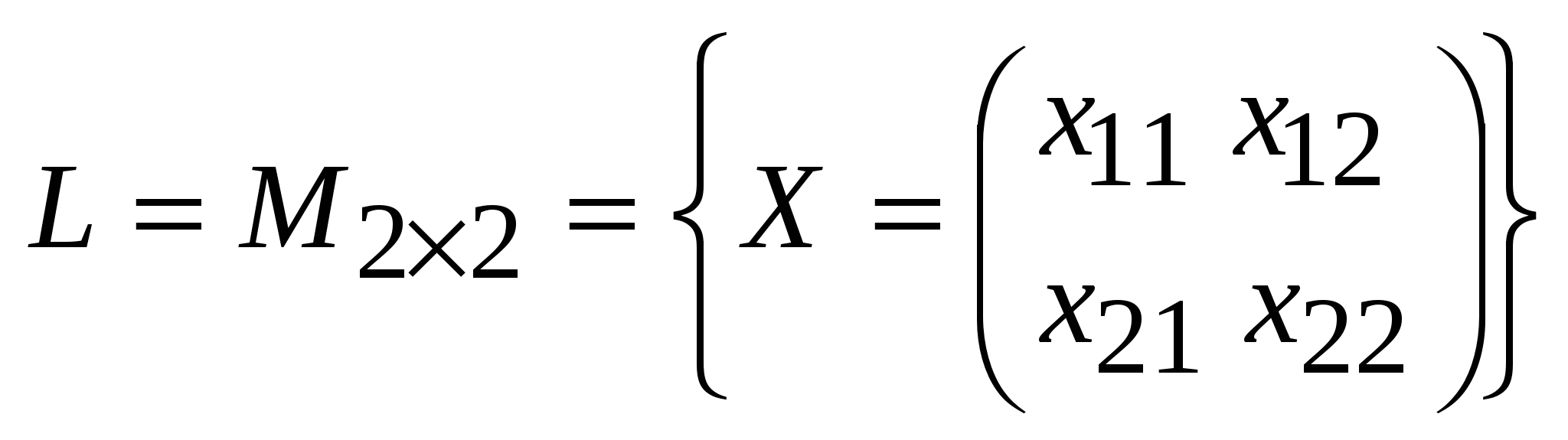 . . 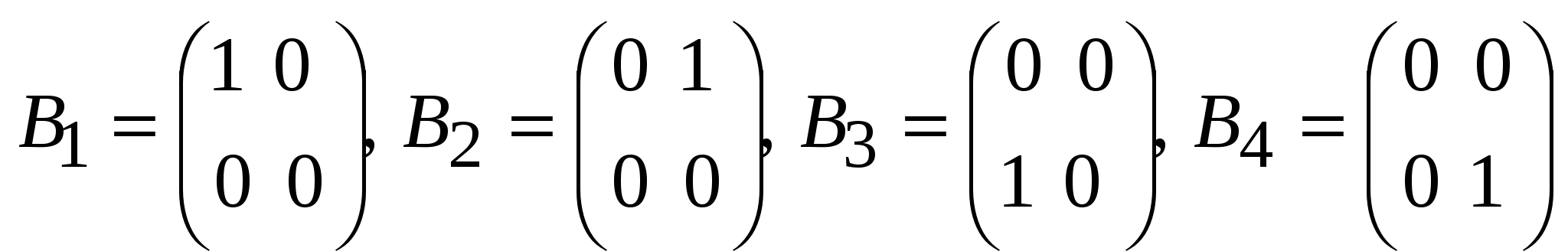 стандартный базис пространства стандартный базис пространства 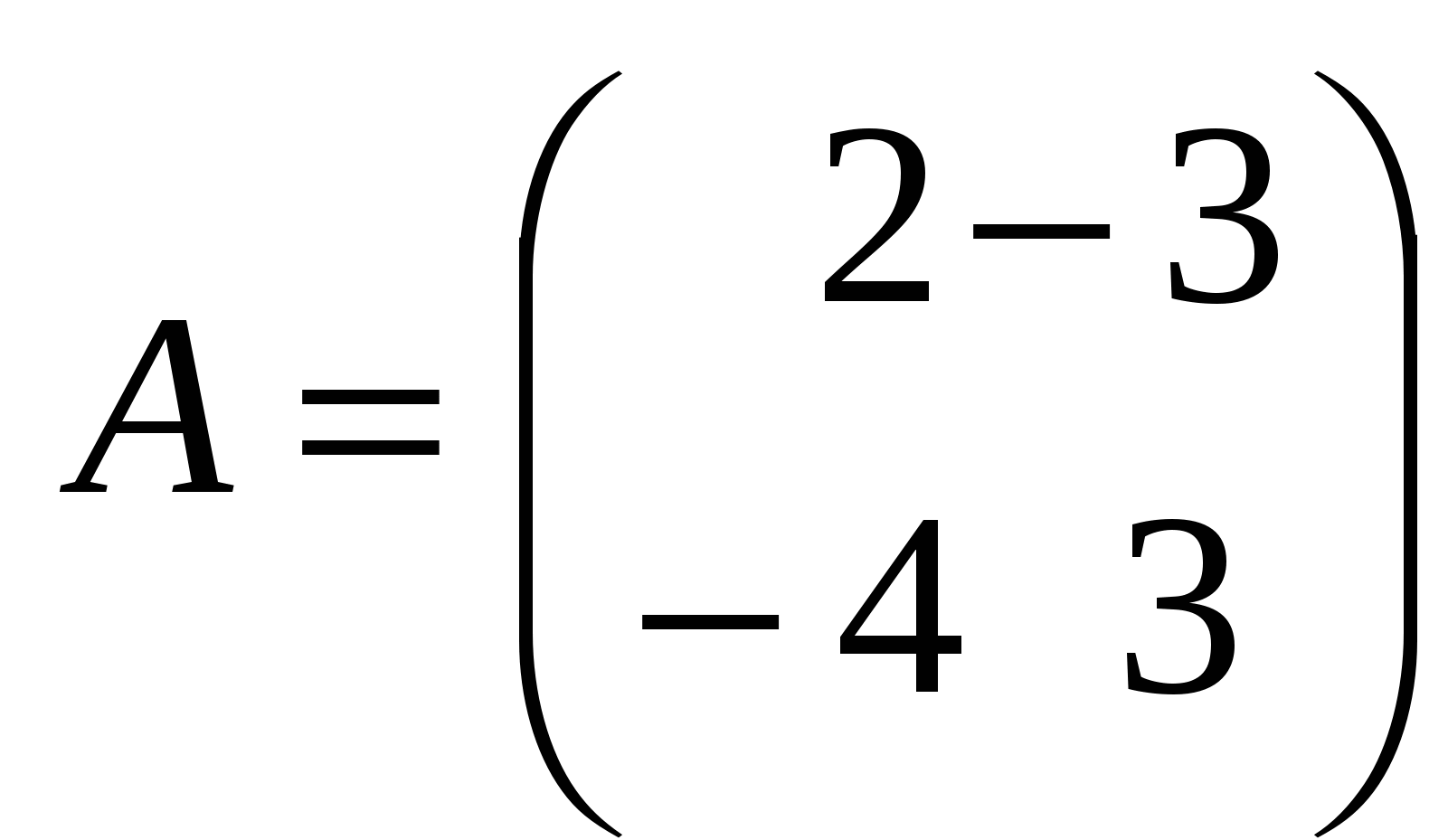 . .Решение. 8.2. Билинейной функцией на линейном пространстве В базисе где Выражение Если Билинейную форму можно записать в векторно-матричной форме где 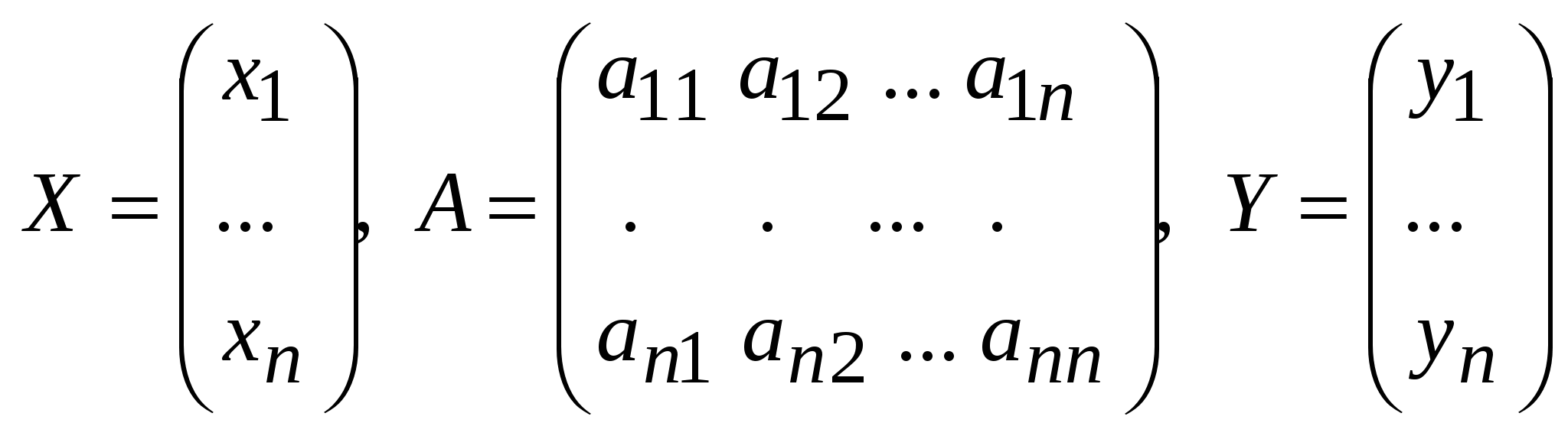 . .Матрица У симметричной билинейной формы матрица При переходе к новому базису в которой 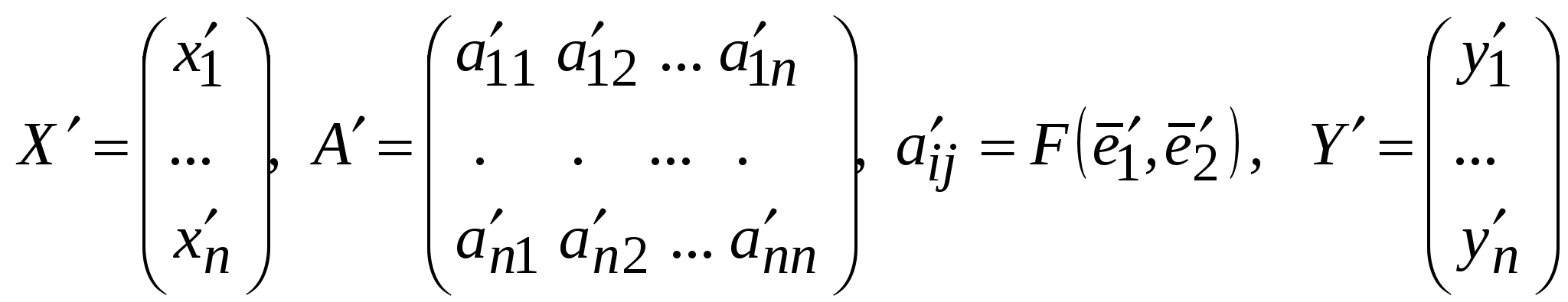 . .Матрицы Здесь Пример 3. На линейном векторном пространстве Решение. Пусть 1) Исследуем функцию Теперь проверим линейность функции Окончательный вывод: функция 2) Исследуем функцию Теперь проверим линейность функции Окончательный вывод: В дополнение приведем векторно-матричное выражение для Здесь Следовательно, 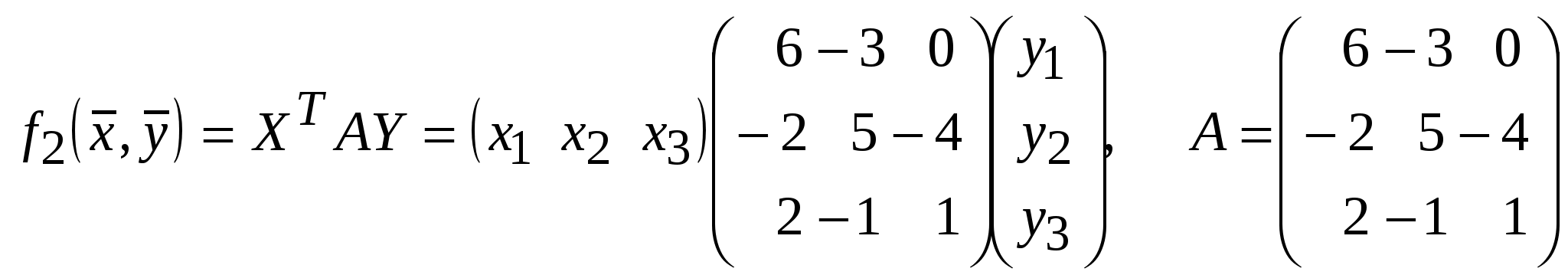 - матрица билинейной функции - матрица билинейной функции Пример 4. Билинейная функция Найти выражение функции Решение. 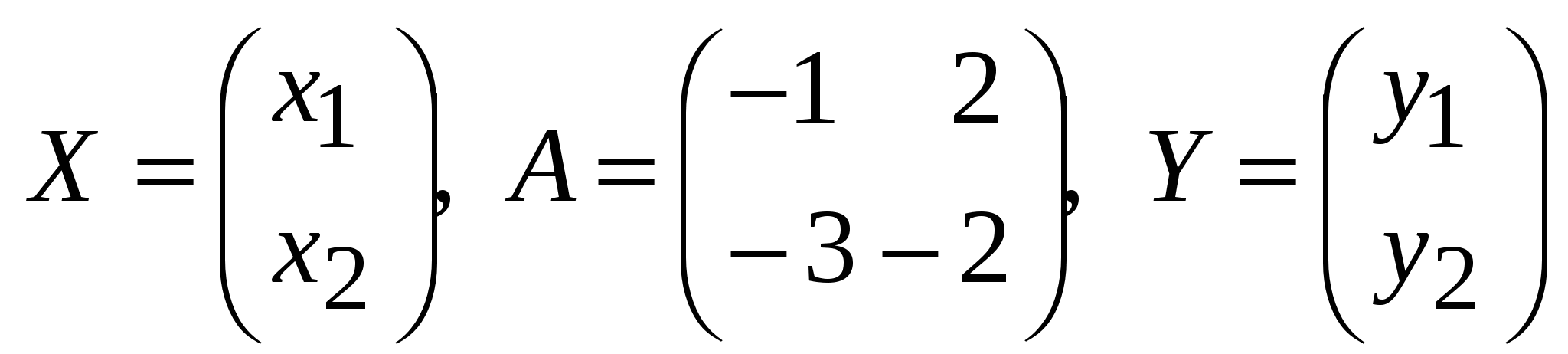 . .Найдем матрицу 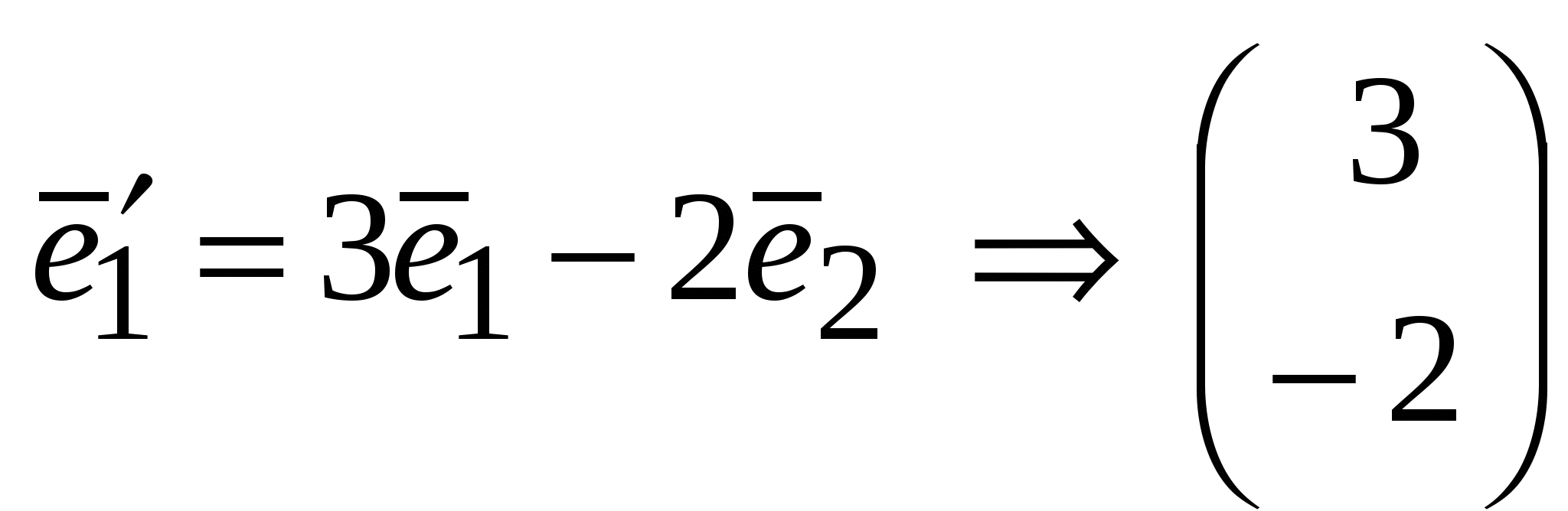 -1-й столбец матрицы -1-й столбец матрицы 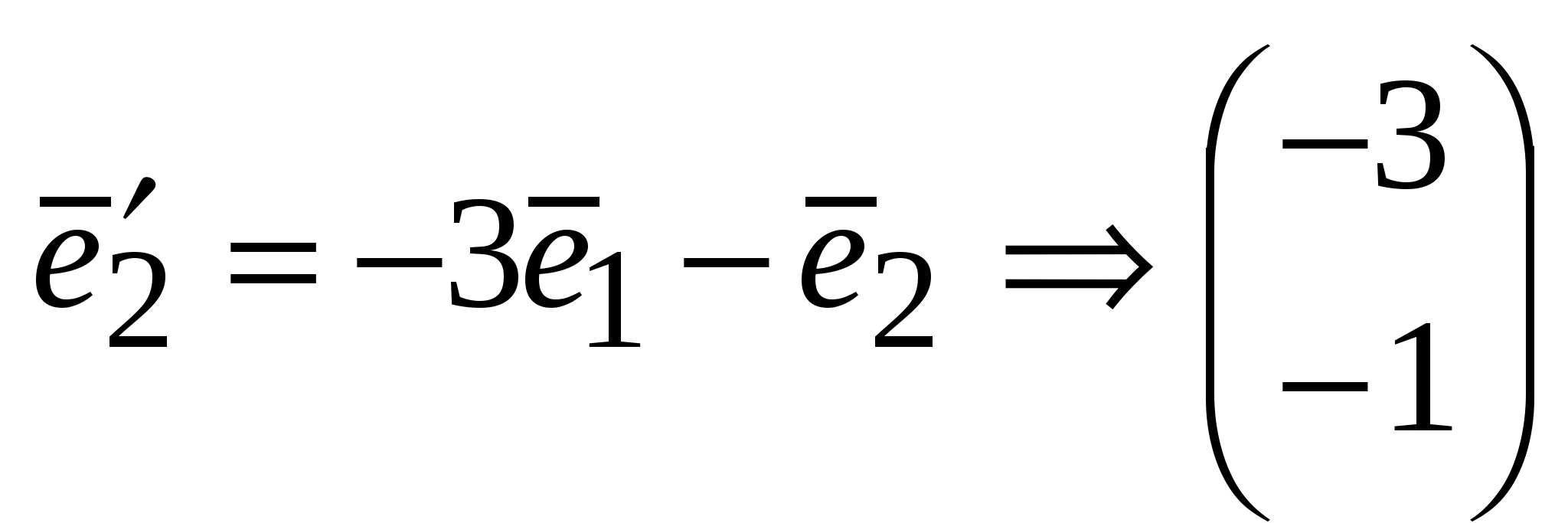 - 2-й столбец - 2-й столбец 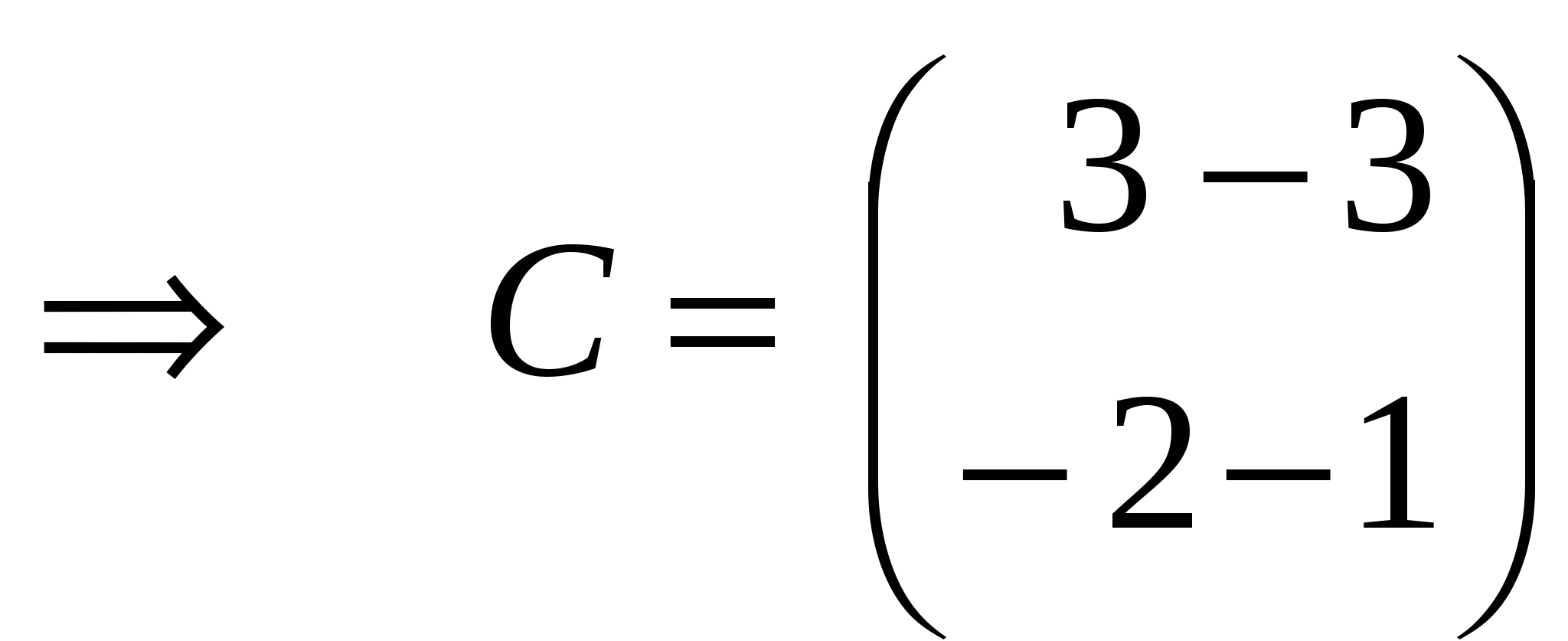 . .По формуле (6) вычисляем матрицу 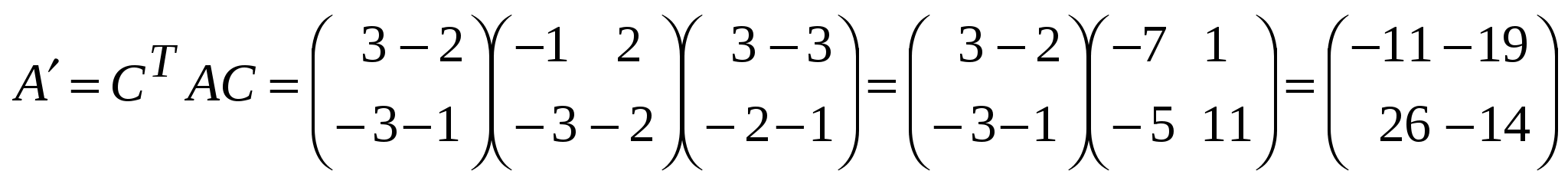 . .В базисе 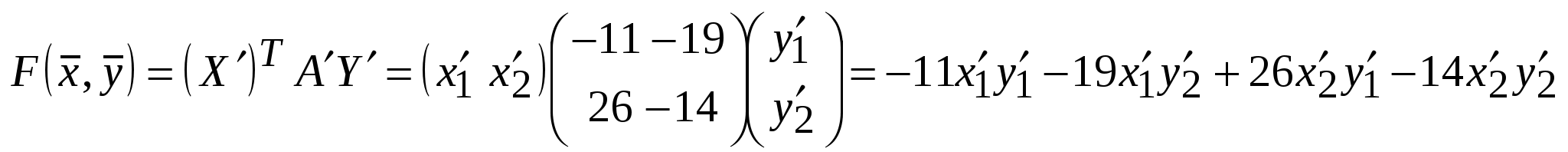 . .Здесь 8.3. Квадратичной функцией Следовательно, В найденном выражении функции Выражение квадратичной функции Пример 5. Найти квадратичные формы соответствующие билинейным формам: Решение. 1) 2) Следует отметить, что две различные билинейные формы могут давать одну и ту же квадратичную форму. Например, билинейные формы приводят к одинаковой квадратичной форме Таким образом, между билинейными и квадратичными формами не существует взаимно однозначного соответствия. Однако, если рассматривать только симметричные билинейные формы Каждой квадратичной форме Пример 6. Найти матрицы квадратичных форм Решение. 1) 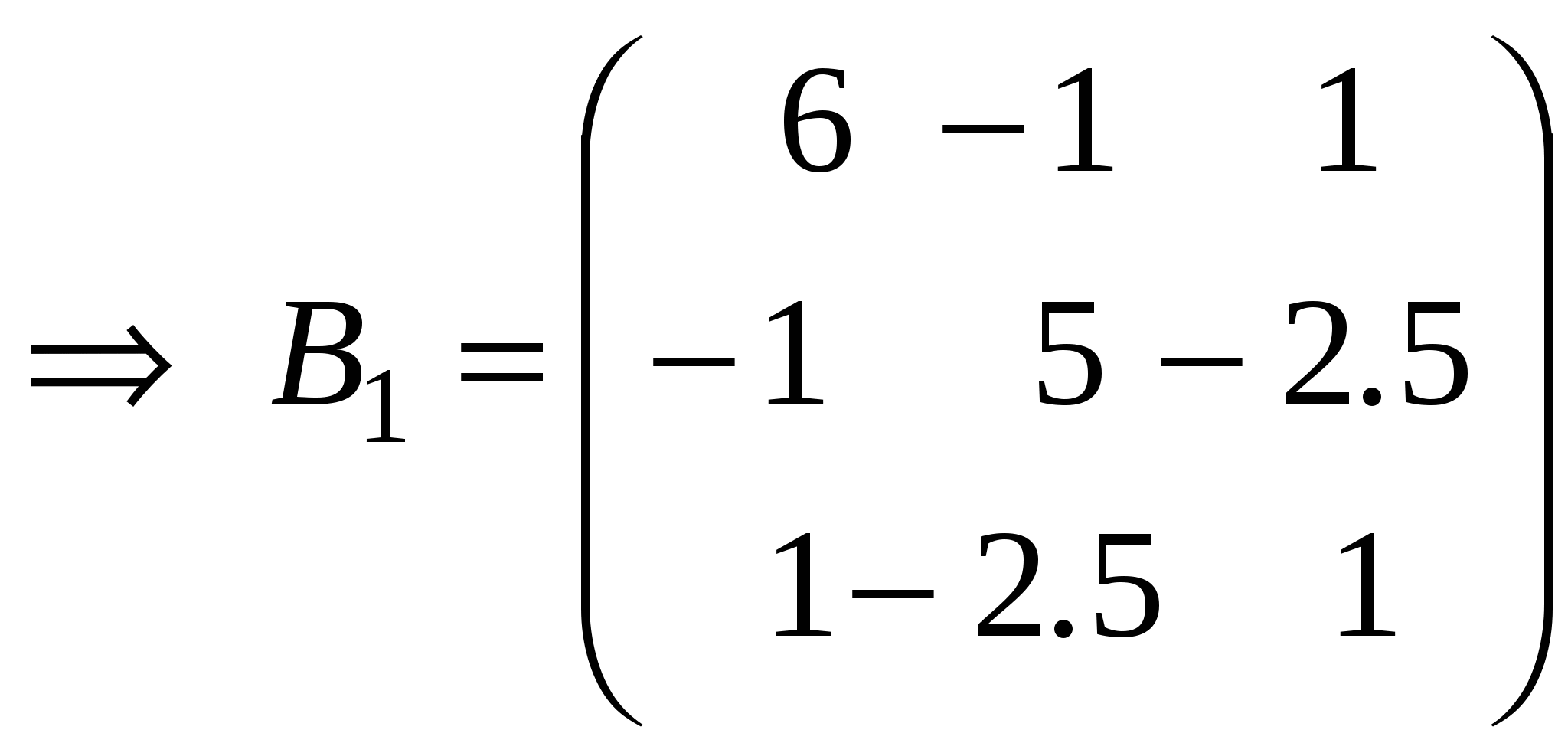 - матрица квадратичной формы - матрица квадратичной формы 2) 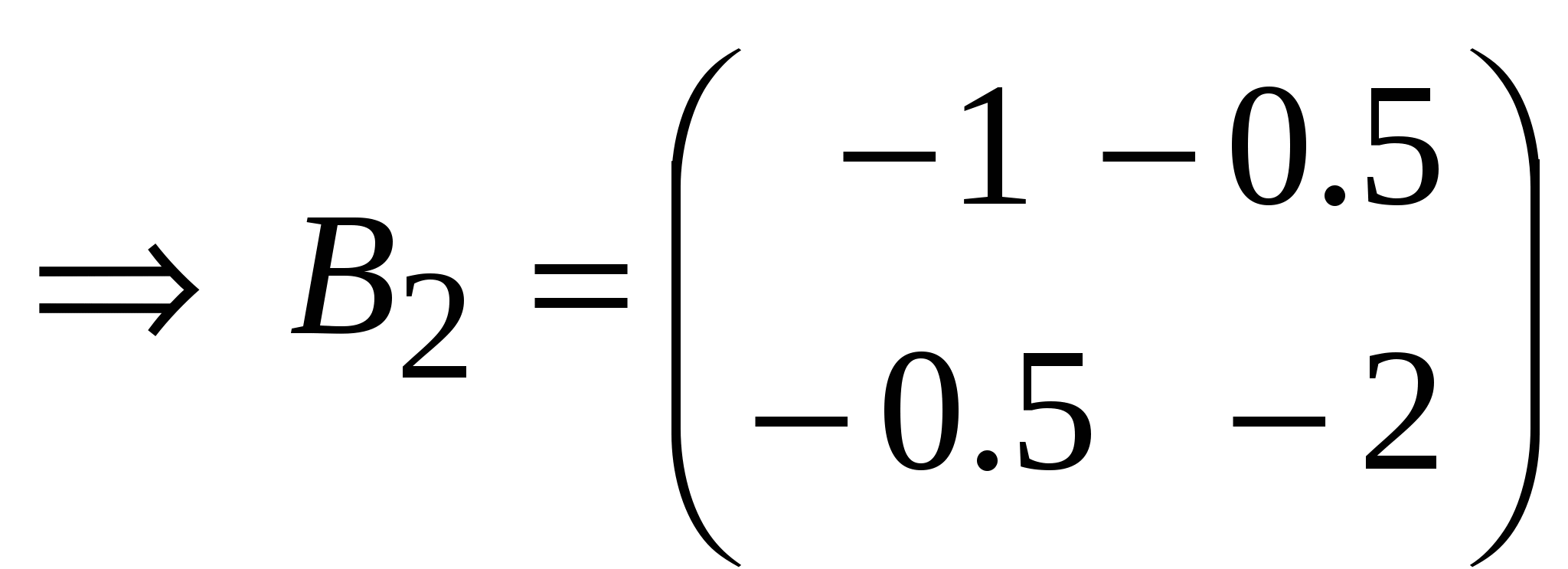 - матрица квадратичной формы - матрица квадратичной формы С помощью матрицы 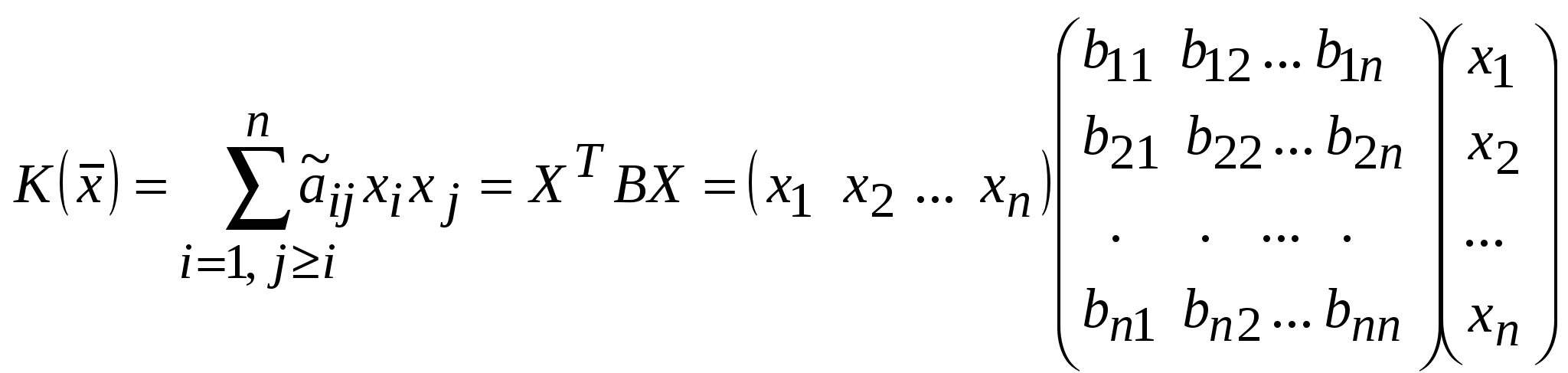 . . Пример 7. Записать квадратичные формы Решение. Воспользуемся матрицами 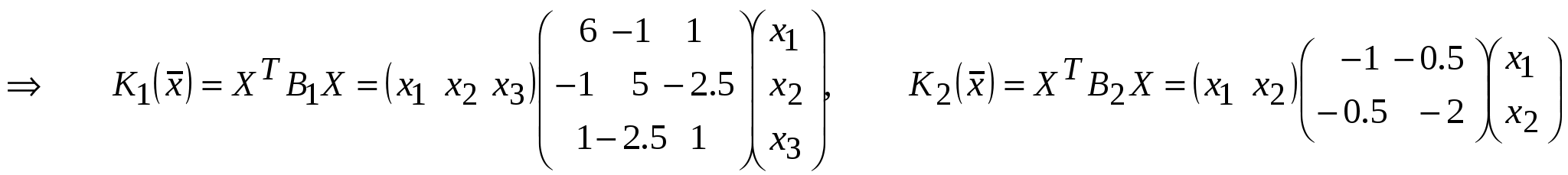 . .При переходе к новому базису где 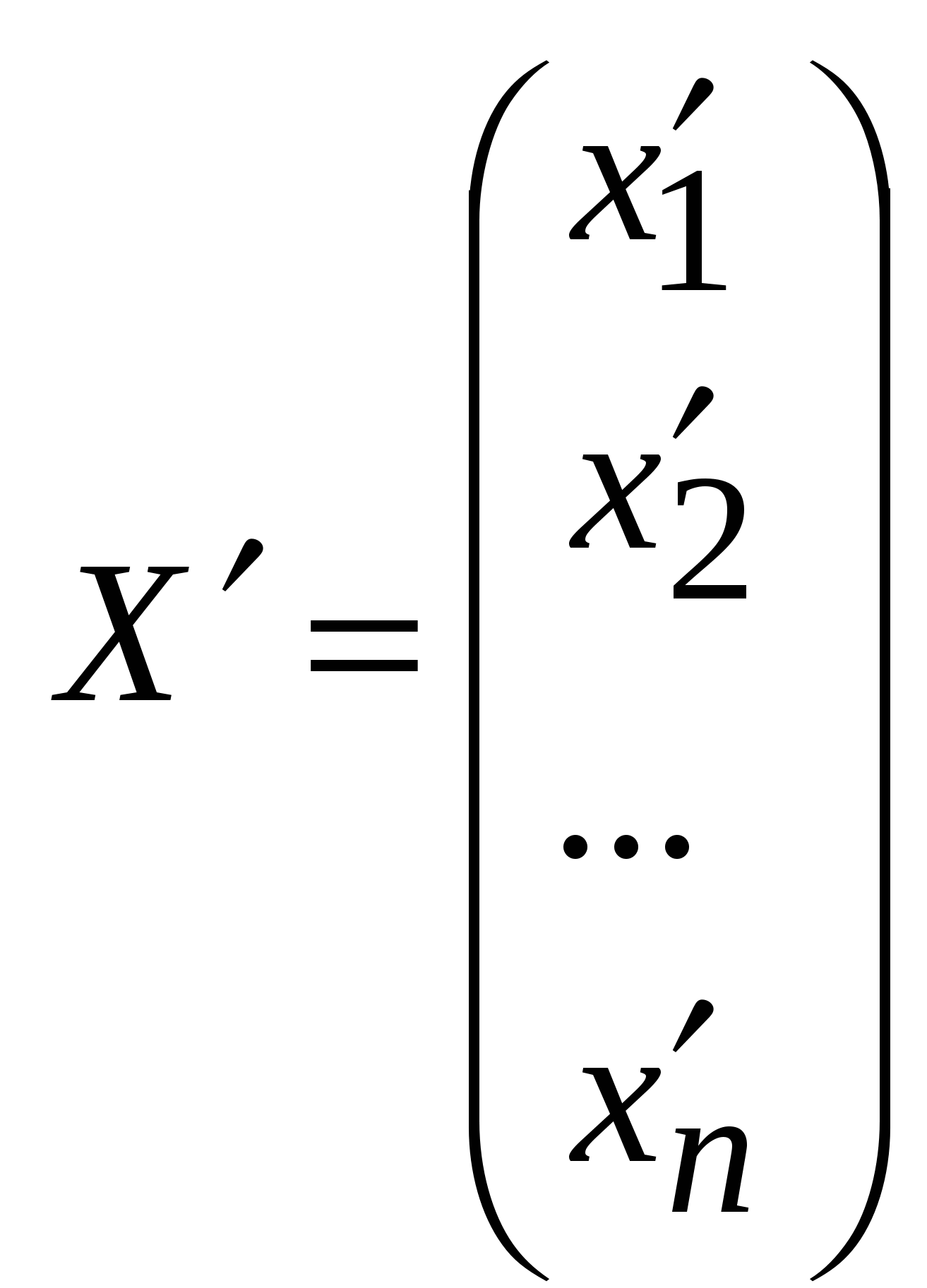 , , Напомним, что старые и новые координаты связаны равенством 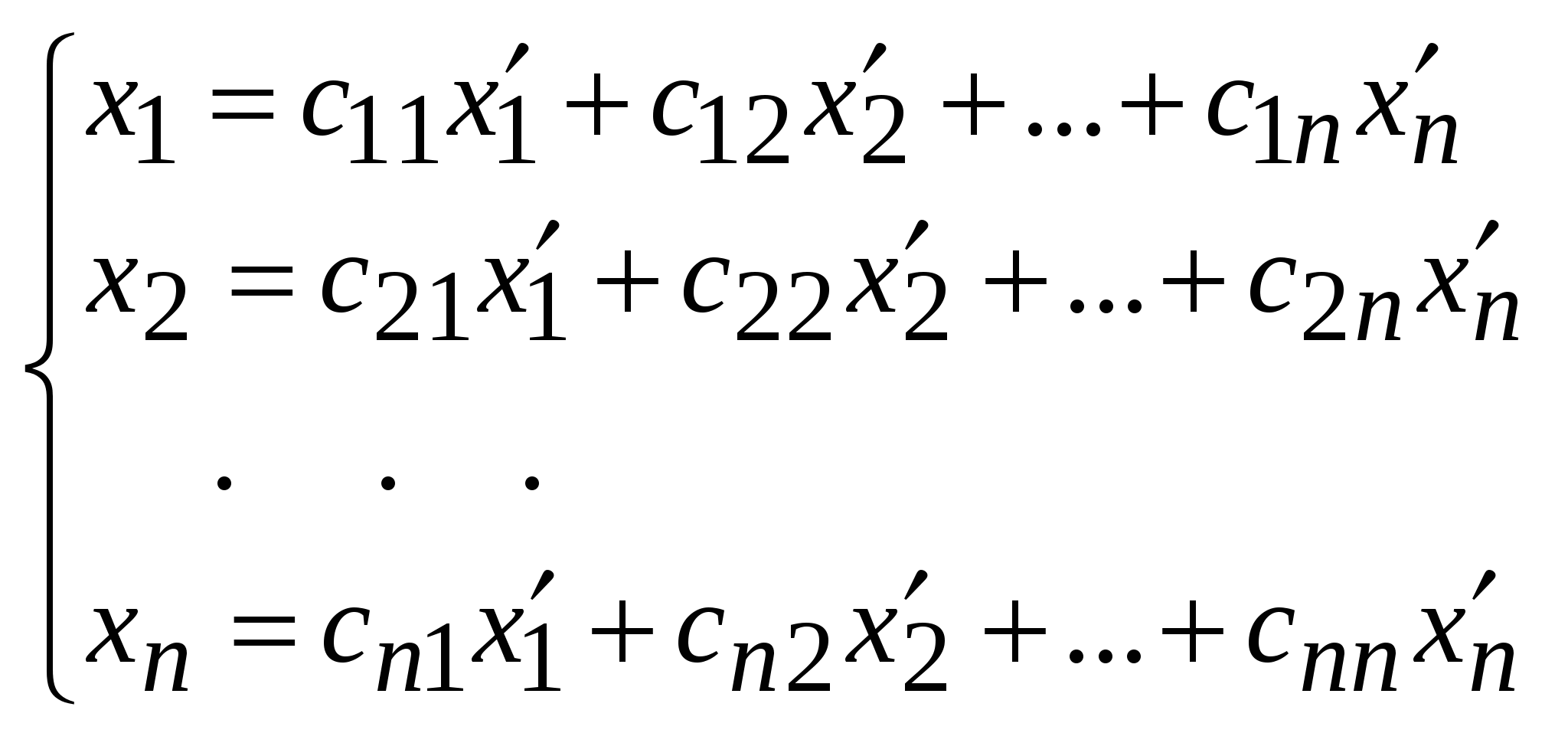 . .Эти формулы называются невырожденным линейным преобразованием координат. _______________________________________________________________ Домашнее задание. 1. Билинейные формы 1.1. 1.2. Найти матрицу билинейной формы, ее матричное представление, а также матрицу и выражение 2. Найти квадратичные формы, соответствующие билинейным формам из примеров 1.1, 1.2. Записать эти квадратичные формы в матричном виде. По квадратичным формам записать соответствующие им симметричные билинейные формы. |
