Предикаты. Занятие 9 Предикаты
 Скачать 76.31 Kb. Скачать 76.31 Kb.
|
|
Практическое занятие №9 Предикаты Цель: Изучить понятие предиката. Научиться выполнять операции над предикатами и находить множество истинности предикатов, записывать высказывания, используя кванторы, и определять их истинность. Теоретическая часть   Пример 1: Даны предикаты, определить их множество истинности 1. «2х+5=3, х  N», тогда I ={Ø} –множество истинности предиката N», тогда I ={Ø} –множество истинности предиката2. «2х+5=3, х  R» тогда I ={-1} R» тогда I ={-1}3. «х<7, х  N» I ={1,2,3,4,5,6}. N» I ={1,2,3,4,5,6}.4. «В многоугольнике х имеется у вершин» - двухместный предикат А(х,у), где х  Х, у Х, у У (Х – множество многоугольников, У= N - множество натуральных чисел (определяет число вершин)) У (Х – множество многоугольников, У= N - множество натуральных чисел (определяет число вершин))Тогда (квадрат, 5)  I, а (квадрат, 4) I, а (квадрат, 4)  I IПример 2. Найти множество истинности действия над предикатами F 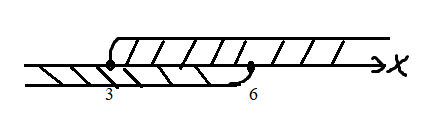 (x): «3 ≤ х», х (x): «3 ≤ х», х  R RQ(x): « х ≤ 6», х  R R а) конъюнкцияIF 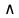 Q: « Q: «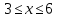 » »б) дизъюнкция I 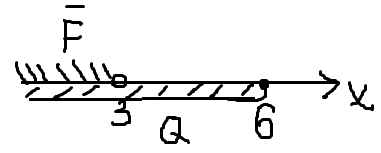 F F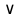 Q: « Q: «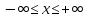 » »в) импликация Пол определению IF 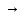 Q= Q= 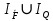 IF 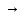 Q : « Q : «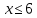 » »Пример 3: Записать предложения с помощью кванторов, и определить их истинность: 1) «Все целые числа кратны 3» т.е. одноместный предикат F(x): «число х кратно 3» . Присоединим квантор всеобщности ( 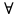 x x X)F(x), так как указано «все», что невозможно, поэтому высказывание ложное – Л. X)F(x), так как указано «все», что невозможно, поэтому высказывание ложное – Л.2) «Некоторые целые числа кратны 3» т.е. одноместный предикат F(x): «число х кратно 3». Присоединяем квантор существования ( 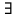 x x X)F(x), так как указано «некоторые», а это действительно и высказывание истинное – И. X)F(x), так как указано «некоторые», а это действительно и высказывание истинное – И.Пример 4. а) X – это множество людей; одноместный предикат F(x): «Рост человека х меньше 180 см». Рассмотрим все варианты навешивания кванторов, определим их истинность: ( 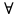 x x  X)F(x) – «У всех людей рост меньше 180 см» - Л X)F(x) – «У всех людей рост меньше 180 см» - Л( 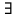 x x  X)F(x) – «У некоторых людей рост меньше 180 см» - И X)F(x) – «У некоторых людей рост меньше 180 см» - И( 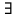 !x !x X)F(x) – «У единственного человека рост меньше 180 см» - Л X)F(x) – «У единственного человека рост меньше 180 см» - Лб) двуместный предикат F(x, y) – «Человек x родился в году y» X – множество людей; Y – множество годов рождения; x  X, y X, y Y Y( 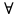 x x X)( X)(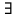 y y  Y)F(x) F(x, y) «Для каждого человека х есть год у, в котором он родился» – И Y)F(x) F(x, y) «Для каждого человека х есть год у, в котором он родился» – И( 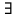 y y  Y)( Y)(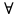 x x X) F(x, y) – «Существует год у, в котором родился любой человек х» - Л X) F(x, y) – «Существует год у, в котором родился любой человек х» - Л( 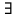 х х  Х)( Х)(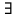 у у Y) F(x, y) – «Существует человек х, который родился в некотором году y» - И Y) F(x, y) – «Существует человек х, который родился в некотором году y» - ИПрактическая часть Задание 1. Найдите множества истинности следующих предикатов, заданных над указанными множествами. № варианта Предикаты 1. «х кратно 3», М= {1, 2, 3, 4, 5, 6, 7, 8, 9}; 2. «х кратно 3», М= (3, 6, 9, 12}; 3. «х кратно 3», М= {2, 4, 8}; 4. «х2 + 4 > 0», М= R; 5. «sin x > 1», Μ = R; 6. «х2 + х - 6 = 0», Μ=R; 7. «х1 < х2», Μ1 = {1, 2, 3, 4, 5}, М2 = {3, 5, 7}; 8. «х1 делит х2», М1 = М2 = {2, 3, 4, 6}; 9. «|х1 | + х2 > 12», Μ1 = {-2, 4, 8}, М2 = {0, 7, 9, 11}; 10. «х1 + х2 < 0», М1 = {-3, -2, -1, 0, 1, 2, 3}, М2 = {-3, 1, 2}; 11. «х2 + 9 < 0», М= R; 12. «cos x > 1», Μ = R; 13. «х1 делится нацело на х2», М1 = М2 = {2, 3, 4, 6}; 14. «х2+2х+1=0 », Μ=R; 15. «(х-5)(х+2)=0», Μ=R. Задание 2. Изобразите на координатной плоскости множества истинности следующих двухместных предикатов, заданных на множестве действительных чисел R.
Задание 3. Изобразите на координатной прямой множества истинности следующих предикатов.
Задание 4. Запишите следующие высказывания и определите, какие из них истинные, а какие ложные, считая, что все переменные пробегают множество действительных чисел:
Задание 5. Рассмотрите все варианты навешивания кванторов на предикат P(x,y) и опишите в словесной форме полученные высказывания. Определите истинность полученного высказывания. P(x,y) определен на множестве людей: «x является родителем y» «x является дочерью y» «x живѐт в одном городе с y» «х является отцом для у» «x является родственником y» «x живѐт в одной стране с y» «x является сыном y» «x живѐт на одной улице с y» «х учится в одной группе с у» «x является дедушкой для y» «x живѐт в одном районе с y» «у является родителем х» «x является бабушкой для y» «у является родственником х» «x является соседом для y» Контрольные вопросы Что называется квантором всеобщности? С помощью, каких слов выражается квантор общности? Что называется квантором существования? С помощью, каких слов выражается квантор существования? Что называется квантором единственности? |

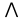 (х < 2)
(х < 2)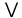 (х < 2)
(х < 2)