Курсовая работа Стрелковский С.П. 493110200003. Защищена с оценкой руководитель зудов Р. И подпись, дата инициалы, фамилия пояснительная записка к курсовой работе численное решение системы нелинейных уравнений По дисциплине Численные методы
 Скачать 103.87 Kb. Скачать 103.87 Kb.
|
|
Санкт-Петербургский политехнический университет Петра Великого Институт электроники и телекоммуникаций Высшая школа прикладной физики и космических технологий КУРСОВАЯ РАБОТА ЗАЩИЩЕНА С ОЦЕНКОЙ ______ РУКОВОДИТЕЛЬ _____________________ Зудов Р.И подпись, дата инициалы, фамилия ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К КУРСОВОЙ РАБОТЕ Численное решение системы нелинейных уравнений По дисциплине «Численные методы» РАБОТУ ВЫПОЛНИЛ Студент гр. № _____________________ подпись, дата инициалы, фамилия Санкт-Петербург, 2022 Оглавление Введение…………………………………………………………………………………………….…….3 Исследуемая система………………………………………………………………………….……3 Аналитическое решение……………………………………………………………………….….4 Решение методом Ньютона………………………………………………………………….….5 Решение методом релаксации….………………………………………………………….…7 Выводы……………………………………………………………………………………………...……10 Введение В этой курсовой работе исследуются различные методы решения систем нелинейных уравнений – трансцендентных уравнений в виде 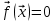 . Требуется сравнить эффективности методов по критерию числа потребовавшихся вычислений в зависимости от заданной точности. . Требуется сравнить эффективности методов по критерию числа потребовавшихся вычислений в зависимости от заданной точности.Исследуемые методы: Ньютона Релаксации (при оптимальном значении параметра релаксации и отличном от него) Исследуемая система:  ДополнениеВся работа проводится в вычислительной среде MATLAB. Вычисления проводятся для трех различных точностей. Критерием останова итерационного процесса считается достижение разницей численных решений i-той и (i-1)-й итераций заданной точности. Аналитическое решениеЧтобы понять верность решений, посчитанных методами Ньютона и релаксации, необходимо изначально самостоятельно решить заданную систему. Для этого воспользуемся онлайн-калькулятором. Прежде всего, нужно понять количество решений системы, так как ее функции с виду периодичны. Для этого построим график. 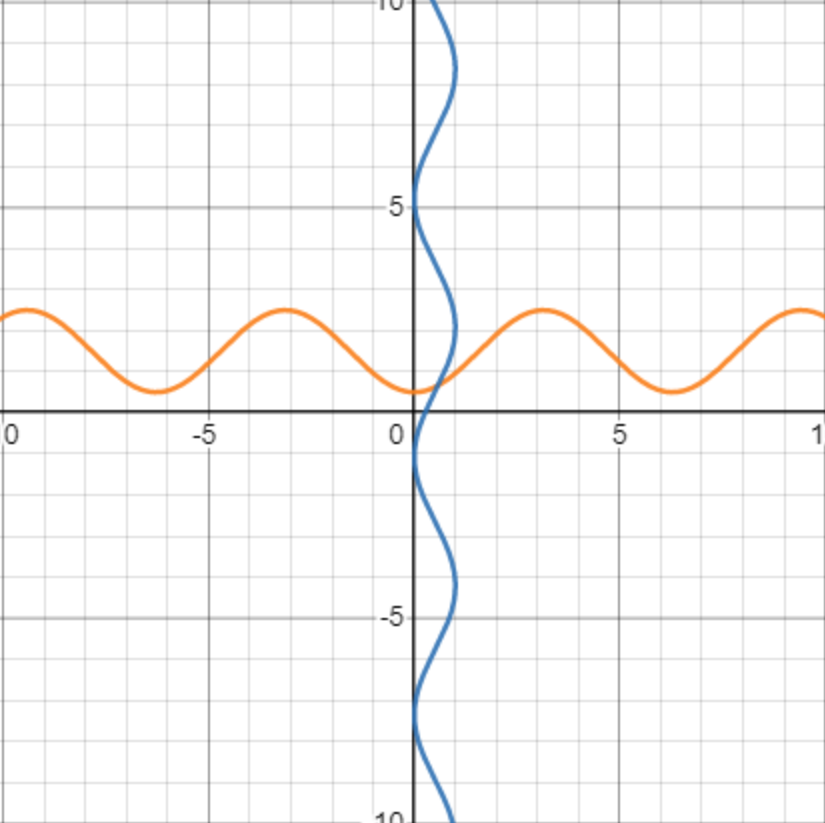 Как можно заметить из графика – Решение всего одно. Можно приступать к поиску решения системы на калькуляторе. 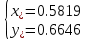 К данным значениям должна сходиться система при ее решении от них будет считаться погрешность при окончании работы цикла итераций. Решение методом Ньютона Из различных источников можно слышать, что метод Ньютона – один из самых эффективных методов поиска численного решения уравнений или их систем. Мы подтвердим это или опровергнем в данном пункте работы. Метод Ньютона – это итерационный численный метод нахождения решения, основанный на построении последовательных приближений по принципу простой итерации. Чтобы численно решить уравнение 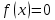 (или подобную систему уравнений выпуклых функций двух и более переменных), его необходимо привести к такой эквивалентной записи, что итерационная процедура вычисления, последовательность которой по теореме Банаха о неподвижной точке стремится к решению, будет иметь вид (или подобную систему уравнений выпуклых функций двух и более переменных), его необходимо привести к такой эквивалентной записи, что итерационная процедура вычисления, последовательность которой по теореме Банаха о неподвижной точке стремится к решению, будет иметь вид 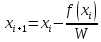 , где , где 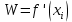 – матрица Якоби, а i – номер итерации. Отсюда очевидно, что W, то есть det(W), должна быть отличной от нуля. Последнее суждение – условие сходимости. – матрица Якоби, а i – номер итерации. Отсюда очевидно, что W, то есть det(W), должна быть отличной от нуля. Последнее суждение – условие сходимости.Метод Ньютона для своего запуска требует начального приближения – вектора значений, лежащих в окрестности точного решения (в данной работе аналитического решения), который подставляется на первой итерации. Пусть и для метода Ньютона, и в дальнейшем для метода релаксации начальным приближением будет точка: 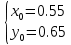 После описания метода, приступаем к вычислениям. Результаты приведем в виде трех таблиц. Первая и вторая – показательные. Они приводят пример работы алгоритма при одной из точностей, включают в себя номер выполненной итерации и значения полученные после исполнения этой итерации. Третья – сводная. Она демонстрирует результаты работы при различных точностях, включает в себя заданную точность, количество исполненных итераций и погрешность значений по итогу работы цикла. Условие сходимости выполнено ( 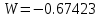 ). ).
Таблица 1. Работа метода Ньютона при точности 10-4.
Таблица 2. Работа метода Ньютона при точности 10-8.
Таблица 3. Работа метода Ньютона при различных точностях. На практике мы увидели, что метод Ньютона работает быстро и точно, достигая значения с погрешностью, близкой к нулю за 3–4 единицы итераций. Решение методом релаксацииО методе релаксации можно сказать, что он является модификацией метода простой итерации и чем-то схож с методом Якоби. Сам метод практически повторяет таковой для линейных. Его суть заключается в дополнительном смещении после вычисления компонент (n+1)-й итерации по формуле метода Зейделя, а итерационная процедура вычисления выглядит так: 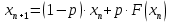 Здесь 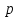 – параметр релаксации. Необходимым условием сходимости является неравенство – параметр релаксации. Необходимым условием сходимости является неравенство 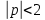 , а достаточным использование оптимального параметра, находящегося по формуле: , а достаточным использование оптимального параметра, находящегося по формуле: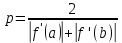 Где a и b это граничные точки окрестности решения. По ним оптимальное значение параметра составляет: 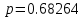 Значение отличного от оптимального параметра возьмем равным: 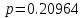 Результаты вычислений предоставлены в шести таблицах для двух параметров аналогично предыдущему способу, где первая и вторая таблицы каждого параметра приводят пример работы алгоритма при одной из точностей, а третья демонстрирует результаты работы при различных точностях.
Таблица 3. Работа метода релаксации с оптимальным параметром при точности 10-4.
Таблица 3. Работа метода релаксации с оптимальным параметром при точности 10-10.
Таблица 4. Работа метода релаксации с оптимальным параметром при различных точностях.
Таблица 5. Работа метода релаксации с отличном от оптимального параметром при точности 10-4
Таблица 5. Работа метода релаксации с отличном от оптимального параметром при точности 10-10
Таблица 6. Работа метода релаксации с отличном от оптимального параметром при различных точностях. ВыводПри сравнении данных, полученных в таблицах, можно заметить, что решение системы может быть достигнуто любым из использованных методов, а также при любой точности. В одинаковых условиях метод Ньютона показывает себя лучше, чем метод релаксации, так как требует меньше итераций. Трудно не отметить тот факт, что при увеличении точности количество итераций возрастает, и в методе релаксации их количество растет на порядок быстрее в сравнении с методом Ньютона, что дает несомненный плюс второму методу. Таким образом при решении данной системы метод Ньютона показал себя значительно лучше и является менее трудозатратным. Список литературы 1. Кудряшова Т. Ю. Численные методы: лекции СПБПУ, 2022. 2. Решение систем нелинейных уравнений в MatLab: Статья - https://codetown.ru/matlab/reshenie-sistem-nelinejnyh-uravnenij/ 3. Релаксационные методы: Статья - http://www.machinelearning.ru/wiki/index.php?title=%D0%A0%D0%B5%D0%BB%D0%B0%D0%BA%D1%81%D0%B0%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D1%8B%D0%B5_%D0%BC%D0%B5%D1%82%D0%BE%D0%B4%D1%8B |
