1-ХГИ МЕТОДИЧКА. збекистон республикаси олий таълим, фан ва инновациялар вазирлиги

• Название: збекистон республикаси олий таълим, фан ва инновациялар вазирлиги
• Дата: 17.05.2023
• Размер: 1.15 Mb.
• Имя файла: 1-ХГИ МЕТОДИЧКА.docx
• Тип: Документы; #1137672
• страница: 1 из 2

ЎЗБЕКИСТОН РЕСПУБЛИКАСИ ОЛИЙ ТАЪЛИМ, ФАН ВА ИННОВАЦИЯЛАР ВАЗИРЛИГИ

ТОШКЕНТ АРХИТЕКТУРА ҚУРИЛИШ УНИВЕРСИТЕТИ

ЖЎРАЕВА ҲУСНОРА ДАВРОНОВНА

ИНЖЕНЕРЛИК ГЕОДЕЗИЯСИ

60210400 – Дизайн (турлари бўйича) 60730900 – Гидротехник қурилиши (турлари бўйича)

60730400 – Муҳандислик коммуникациялари қурилиши ва монтажи (турлари бўйича)

60730200 – Шаҳар қурилиши ҳамда коммунал инфратузилмани ташкил этиш ва бошқариш

60731000 – Қиймат инжиниринги ва кўчмас мулк экспертизаси

Тошкент – 2022

Муаллиф:

ЖўраеваҲуснораДавроновна
“Инженерлик геодезияси” услубий кўрсатма ва топшириқлар

Тақризчилар:

Д.У.Тағаева – ТАҚИ “Геодезия ва кадастр” кафедраси доценти

Д.Б.Усмонов – “ЎзГАШКЛИИТИ” ДУК етакчи мутахассиси


Ушбу услубий кўрсатма 60210400 – “Дизайн (турлари бўйича)”, 60730900 – “Гидротехник қурилиши (турлари бўйича)”, 60730400 – “Муҳандислик коммуникациялари қурилиши ва монтажи (турлари бўйича)”, 60730200 – “Шаҳар қурилиши ҳамда коммунал инфратузилмани ташкил этиш ва бошқариш”, 60731000

– “Қиймат инжиниринги ва кўчмас мулк экспертизаси” бакалавриат йўналиши 2 – курс талабалари учун мўлжалланган.

Ушбу услубий кўрсатмада “Туташ теодолит йўли координаталарини ҳисоблаш” ҳисоб график ишининг ҳисоблаш натижалари кўрсатилган.


ТАҚИ, 2023

ТУТАШ ТЕОДОЛИТ ЙЎЛИ КООРДИНАТАЛАРИНИ ҲИСОБЛАШ

Ишдан мақсад: Туташ теодолит йўли координаталарини ҳисоблаш жадвалини ишлашни ўрганиш.

1. 
   Теодолит йўли бурчаклари ва чизиқларини ўлчашнинг дала журнали.
   
2. 
   Теодолит йўлини ўтказиш журналини ишлаш (теодолит йўли нуқталари координатларини ҳисоблаш).
   

Ишнибажаришучункўрсатма

Туташ теодолит йўли координаталарини ҳисоблашда талаба дала журналини ва уни тўлдириш тартибини билиши керак.

Туташ теодолит йўли координаталарини ҳисоблаш жадвалини ишлаш.

Дастлаб А–4 форматдаги қоғозга қора рангда (туш билан) “туташ йўли координаталарини ҳисоблаш жадвали” чизилади (1 – иловага қаранг)

Жадвални 1 – устунига йўл қирраларидаги нуқта номери, 2-устунига теодолит

йўли қирраларида ўлчанган ички бурчакларининг <2 ва <4 чи бурчаклар ^_i

қийматлари, 6-устунга теодолит йўли томонларининг горизонтал қуйилиши ва 13,14-устунларга бошланғич нуқта (1-нуқта)нинг координата қийматлари талаба вариантига мос тарзда ѐзиб қўйилади.

Шунингдек жадвални 4-устунига теодолит йўлининг 1 – 2 томони дирекцион

бурчаги ^_1.2

ни қиймати вариантга мос тарзда ѐзиб қўйилади.

Ҳисоб ишлари дала ўлчаш натижалари сифатига баҳо беришдан бошланади. Бунинг учун теодолит йўли қирраларида ўлчанган бурчак β ларни йиғиндиси _  _yтопилади.

^y

 899⁰57,7'

Ушбу йиғиндининг қийматида хато бор йўқлигини билиш мақсадида уни назарий жиҳатдан нечига тенг эканини билиш керак.

Назарий жиҳатдан туташ геометрик шакл ички бурчаклар йиғиндиси

_ 180⁰ (n 2)

(1)

Бизнинг мисолидаги туташ теодолит йўли қирралари сони n=7 та, демак,

^наз

180⁰(7  2)  900⁰00'

Ўлчанган бурчаклар хатоси 2 – формула орқали ҳисобланади

Бизнинг мисолда

^f ^ ^улч^ ^наз

(2)

f_  899⁰57,7  900⁰00,0'  2,3'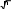

Ушбу мавжуд хатони кўп ѐки кам эканлигини билиш мақсадида (3) формула орқали чекли хато қийматини ҳисоблаймиз ва уни мавжуд хато билан таққослаймиз


f

чек

 3  t

(3)

Бунда t–бурчак ўлчаш аниқлиги; n–бурчаклар сони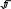

Бизнинг мисолда бурчаклар 2Т30 теодолити билан ўлчанган, демак бурчак ўлчаш аниқлиги 30″, бурчаклар сони 7та бўлгани учун бурчак ўлчашни чекли қиймати қуйидагига тенг бўлади:


f  

чек

 2,6

y
Мавжуд хато –2,3 ±2,6 дан ортмаганлиги учун ўлчаш натижалари қониқарли

деган хулосага келамиз. Мавжуд хато йўқотиш мақсадида ўлчанган бурчакларга тескари ишорада тарқатамиз.

f_ ни йўл қирраларида

Бизнинг мисолда мавжуд хато

• 
  2,3' ^{, демак бериладиган тузатма}
  

 0,4

^ва  0,3

дан тузатма берамиз. Киритилувчи тузатма қийматини 2-устунига ѐзилган ўлчанган бурчаклар қийматлар қийматларини юқорига майда рақамлар билан ѐзиб қўйилади.

Тузатма тарқатишда узун томонлар орасида ўлчанган бурчакларга кўпроқ қиймат беришга ҳаракат қилинади.

Тарқатма тузатмаларининг йиғиндиси тескари ишора билан

керак, яъни

_f га тенг бўлиши

__

  f_

(4)

Жадвални 4 – устунга дирекцион бурчаклар ѐзилади. Ушбу устунни 1 ва 2

1.2
қирра оралиғига 1 – 2 томонининг дирекцион бурчак аниқланиб ѐзиб қўйилади.

^12

вариантга мос тарзда

Бизнинг мисолда

  34⁰07,0'

шундан кейин ушбу 4 – устунни пастки

қаторларига

^ 2,3 ^,3,4 ^, 4,5 ^,5,6 ^, 6 ^,

ѐзилиши керак. Ушбу дирекцион бурчак

қийматларини (5) ѐки (6) формулалар орқали ҳисобланади.

Ўлчанган β бурчаклар ўнг томонда бўлганда “ўнг бурчак” формуласи қўлланади.

^ 2,3

^ 3,4

^{ }1,2

^{ } 2,3

 180⁰   ^


2

3 _
 180⁰   ^

0

(5)

 _4,5   _3,4  180   _{4 }

^ 5,6

^ 6,1

^{ } 4,5

^{ } 5,6

 180⁰  

 180⁰  



5 <sub>

6</sub> _

Ўлчанган β бурчаклар чап томонда бўлганда “чап бурчак” формуласи қўлланади.

^ 2,3

^ 3,4

^{ }1,2

^{ } 2,3

  ₂

 ₃

 180^{0 }



 180^{0 }

0

(6)

 _4,5   _3,4   ₄  180 _

^ 5,6

^ 6,1

^{ } 4,5

^{ } 5,6

 ₅

  ₆

 180^{0 }



^{ 1800} _

Ҳисобланган дирекцион бурчакларни тўғри топилганини назорат қилиш учун

(7) ѐки (8) формуладан фойдаланамиз


6,1 1 1,2
 180⁰     , (7)


6,1 1 1,2
   180⁰   , (8)

(7) формула

^_i^ ўнг бўлганда, (8) формула эса

^_i^ чап бўлганда ўринлидир.

Бизнинг мисолда ўлчанган бурчаклар “чап бурчак” бўлганлиги сабабли дирекцион бурчак аниқлашда 6-формуладаги элемент 2-қатор формуласида ҳам иштирок этгани сабабли ҳисоблашларни устун кўринишда ѐзиб бериш қулайроқдир.

Бизнинг мисолда

^1,2 ^

34⁰07,0'

ПП187
   157⁰34,3

_ 191⁰41,3'

  180⁰00,0'

^ 2,3 ^

11⁰41,3'

ПП187
   130⁰57,7

_ 142⁰39,0'

  180⁰00,0'

^3,4 ^

322⁰39,0'

Топилган дирекцион бурчаклар қиймати 360⁰ дан катта бўлса, улардан 360⁰ олинади ва аниқланган кичик қиймат жадвалга уларнинг ўртасига ѐзилади.

Жадвални 5 – устунга румблар ѐзилиши керак. Румб қийматларини аниқлаш учун “дирекцион бурчак ва румб орасидаги муносабат” жадвалидан (1-жадвал) фойдаланиб дирекцион бурчак чорагига мос тарзда румблар номланади ва қиймати чорагига мос формула билан ҳисобланади.

Бизнинг мисолда румблар қуйидагича топилади:

(1-жадвал)

Румб	Дирекцион бурчак
I- чорак: ШШқ r 	I- чорак: ШШқ   r
II-чорак: ЖШқ r 1800  	II-чорак: ЖШқ   1800  r
III-чорак: ЖҒ r  1800	III-чорак: ЖҒ   1800  r
IV-чорак: ШҒ r 3600  	IV-чорак: ШҒ   3600  r

^ПП187,1

 11⁰41,3'

^rПП187,1

 11⁰41,3'

^1,2

^2,3

^3,4

^4,5

^5,6



 322⁰39,0'

 247⁰25,9'

 223⁰57,7'

 150⁰58,1'

 145⁰25,0'

 63⁰20,8'

^r1,2 ^r2,3 ^r3,4 ^r4,5 ^r5,6

r

 37⁰21,0'

 67⁰25,9'

 43⁰57,7'

 29⁰01,8'

 34⁰35,0'

 63⁰20,8'

6, ПП187 6, ПП187

Жадвални 6 – устунига ѐзилган йўл томонлари горизонтал қўйилишларининг йиғиндиси олиниб полигон периметри Р аниқланади ва устун тагига ѐзилади.

Бизнинг мисолда Р=356,67+191,00+259,25+201,96+165,92+254,28+221,28 = 1650,86 м

Жадвалнинг 7-графасига sinα ва cosα ҳисоблаб топилади. Бунда 3-графадаги тўғриланган ўлчанган бурчаклардан sinα ва cosα қиймат ҳисоблаб топилади

Жадвални 9 ва 10 графаларига мос тарзда ∆х ва ∆у координата орттирмалари қуйидаги формулалар ѐрдамида ҳисоблаб топилади.

^{ xn dn cos}_n; (9)

^{ yn dn sin}_n; (10)

Координата орттирмаларининг ишоралари микрокалькулятор ѐрдамида ҳисоблаш жараѐнида маълум бўлади. Ҳисоблашда аниқланган ишоралар тўғри аниқланганлигини румб чорагига қараб 1 – жадвал бўйича текшириш мумкин.

Бизнинг мисолда


ПП187,1 ПП187,1 ПП187,1
_{ y  d  sin } 356,67 (–0,20258) = +72,26


ПП187,1 ПП187,1 ПП187,1
_{ x  d  cos } 356,67 (+0,97927) = +349,28


1,2 1,2 1,2
_{ y  d  sin } 191,00 (–0,60668) = –115,88

 x_1,2

^{ d}1,2

 cos

1,2

_ 191,00 (+0,79494) = +151,83

_{ y3,4  d2,3  sin 2,3 } 259,25 (–0,92342) = –239,40

2,3 2,3 2,3
_{ x  d  cos } ^259,25 ^{(–0,38379) = –99,50}


3,4 3,4 3,4
_{ y  d  sin } ^201,96 ^{(+0,69418) = –140,20}


3,4 3,4 3,4
_{ x  d  cos } ^201,96 ^{(–0,71980) = –145,37}


4,5 4,5 4,5
_{ y  d  sin } ^165,92 ^{(+0,48527) = +80,52}


4,5 4,5 4,5
_{ x  d  cos } ^165,92 ^{(+0,87437) = –145,08}


5,6 5,6 5,6
_{ y  d  sin } ^254,78 ^{(+0,56760) = +144,61}


5,6 5,6 5,6
_{ x  d  cos } ^254,78 ^{(-0,82330) = -209,76}


6, ПП187 6, ПП187 6, ПП187
_{ y  d  sin } ^221,28 ^{(+0,89374) =+197,75}


6, ПП187 6, ПП187 6, ПП187
_{ x  d  cos } ^221,28 ^{(+0,44859) =+99,26}

Ҳисоблаб топилган координата орттирмаларини юздан биргача яхлитлаб жадвалнинг 8 ва 9 устунни мос қаторига ѐзилади. 8 устундаги ∆y қийматлари маъноси жиҳатидан y ўқи бўйича теодолит йўли қирраларининг фарқини англатади. Уларнинг арифметик йиғиндиси назарий жиҳатидан охирги ва бошланғич қирра координаталари фарқига тенг бўлиши керак. Полигон яъни туташ йўлларда бошланғич нуқта охирги нуқтани ўзига эга бўлади. Шу сабабли уларни фарқи

_у_наз у_ох у_бош 0 бўлади.

Амалда ∆y ларни арифметик йиғиндиси 0 ѐки бирор бошқа сонга тенг бўлади.

Ушбу сонни _у_амалдеб белгиласак, yбўйича хатолик қуйидагича аниқланади.

^fу^ ^уамал^ ^уназ

Бизнинг мисолдаги туташ йўл учун

^fу^ ^уамал^ ^уназ⁼ ^уамал^{ 0 } ^уамал

f_x _у_амал 0,33  0  0,33

бўлади

(11)

Жадвални 9 – устунидаги ∆xқийматлари маъноси жиҳатидан xўқи бўйича теодолит йўли қирраларининг фарқини англатади. Полигон яъни туташ йўлларда

_х_наз 0 бўлгани учун xўқи бўйича хатолик қуйидагига тенг бўлади.

^fх^ ^хамал^ ^хназ

^ ^хамал

(12)

f_х _х_амал (0,06)  (0)  0,06м

хва уўқлари асосида 12 – формула ѐрдамида аниқланган умумий йўл периметри бўйича боғланмаслик хатоси ҳисобланади.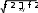

f_P  ⁽¹²⁾

Бизнинг мисолда

f_P  

 0,76

Ҳисобланган йўл периметри боғланмаслик периметрига таққослаш орқали бажарилган ишнинг нисбий хатосини аниқлаймиз:

f_p

^fнисб ^ _P

(13)

Аниқланган нисбий хато чекли нисбий хато қийматидан ортмаслиги керак.

Чекли хато теолоит йўли учун

¹ бўлади, демак

2000

^fнисб ^

f_P

P

1


2000

Бизнинг мисолда

^fнисб^

f_P

P

0,76 _

1650,86

1 _

2200

1


2000

f_x, f_y, f_P <sup>ва

f</sup>нисб

катталикларини ҳисоблашлар координата ҳисоблаш

жадвалини тагида келтирилади. Агар

^fнисб

_ 1

2000

шарти бажарилса ҳисоб ишлари

давом эттирилади, акс ҳолда иш нотўғри бажарилган деган хулосага келинади.


y
^f_x ва _fорттирма боғланмаслик хатолари йўл томон узунликларига

пропорционал тарзда ∆х ва ∆уорттирмаларига тескари ишорада тарқатиб чиқилади.

∆хорттирмаларига тузатма (14) формула орқали, ∆уорттирмаларига тузатма

(15) формула орқали аниқланади.

^x_n

^y_n

 ^{ fx}  d

_P n

 ^{ fy} d

_P n

(14)
(15)

Бу ерда Р– йўл периметри юзлик метрда,

d– томон узунлиги юзлик метрда,

n– ПП187.1, 1.2, 2.3, 3.4, 4.5, 5.6, 6.ПП187 – йўл томонлари индекси.


y
Топилган тузатмалар ҳар бир координата орттирмасини устига майда рақамлар билан ѐзиб қўйилади. Тарқатилган тузатмалар йиғиндиси тескари ишора

билан боғланмаслик хатолари

^fxва

_fга тенг бўлиши керак.

__x  f_x;

Бизнинг мисолда

__y  f_y

(16)

^yПП187.1

  f_{y d}P



=
ПП187.1

• 
  f_{у d}P
  

ПП187.1

^0,33  356,67 _=+0,07

1650,86

^y1.2

  f _{y d}P

1.2 ⁼

• 
  f_{у d}P
  

1.2

^0,33 191,00 _=+0,04

1650,86

^y2.3

  f _{y d}P

2.3 ⁼

• 
  f_{у d}P
  

2.3

^0,33  259,25_=+0,05

1650,86

^y3.4

  f _{y d}P

3.4

• 
  f_{у d}P
  

3.4

^0,33  201,96 _{= +0,04}

1650,86

^y4.5


  f _{y d}P

• 
  f_{y d}
  

4.5 ⁼
=

• 
  f_{у d}P
  
• 
  f_{у d}
  

4.5

^0,33 165,92 _{= +0,04}

1650,86

^0,33  254,78 _{= +0,05}

^y5.6 ^ _P

5.1

_P 5,6

1650,86

^y6. ПП187

  f_{y d}P

6.ПП187 ⁼

• 
  f_{у d}P
  

6.ПП187

^0,33  221,28 _{= +0,04}

1650,86

^x

ва _y

ҳисоблашда улар юздан бир хонагача яхлитлаб олинади.

Координата ҳисоблаш жадвалини 11 ва 12 устунларига ∆х ва ∆у орттирмалари тузатилган ҳолда ѐзиб чиқилади. Тузатилган координата орттирмаларини йиғиндиси

мос тарзда _x_наз

^ва ^уназ

қийматларига тенг бўлиши керак.

Тузатилган координата орттирмалари ҳисоблаб топилган координата орттирмасига тузатмаларни алгебраик қўшиш орқали топилади.

^{xтуз x x}_

(17)

^утуз

 у 





у_

Тузатилган координата орттирмаларини йиғиндиси _x_наз

^ва ^уназ

қийматларига тенг чиқиши ишни тўғри бажарилганини кўрсатади. Туташ йўл (полигон) да ушбу йиғиндиларни ҳар бири нолга тенг бўлиши керак, яъни

_x_наз 0; _у_наз 0

Бизнинг мисолда

_у_туз (72,33)  (115,84)  (239,35)  (140,16)  (80,56)  (144,66)  (197,80)  0

_x_туз (349,14)  (151,75)  (99,60)  (145,45)  (145,15)  (209,86)  (99,17)  0

Шундан сўнг йўл нуқталари координаталари ҳисобланади. Бунинг учун йўлнинг бошланғич нуқтаси координаталарини оламиз ва унга таянган ҳолда қуйидаги ифодалардан фойдаланиб, қолган нуқта координаталарини ҳисоблаймиз.

Бизнинг мисолда

^Xn^{ X}n1 ^{ X}nn1

^Yn^{ Y}n1 ^{ Y}nn1

x₁  x₁

 x
ПП187,1

_ 10000+72,33 = 10072,33

4 3 3,4

5 4 4,5
^{x2  x1  x1.2 } 10072,33 – 115,84 = 9956,49 ^{x3  x2  x2.3 } 9956,49 – 239,35 = 9717,14 _{x x x} 9717,14 – 140,16 = 9576,98 _{x x x} 9576,98 +80,56 = 9657,54


6 5 5,6
_{x x x} 9657,54 + 144,66 = 9802,20


ПП187 6 6, ПП187
_{x x x} 9802,20 + 197,80 = 10000

1 1 ПП187,1
_{y y y} 10000 + 349,14 = 10349,14

^{y2  y1  y1.2 } 10349,14 +151,75 = 10500,89


4 3 3,4

5 4 4,5

6 5 5,6
^{y3  y2  y2.3 } 10500,89 – 99,60 = 10401,29 _{y y y} 10401,29 – 145,45 = 10255,84 _{y y y} 10255,84– 145,15 = 10110,69 _{y y y} 10110,69 – 209,86 = 9900,83


ПП187 6 6, ПП187
_{y y y} 9900,83 + 99,17 = 10000

Ҳисобни текшириш учун

^xПП187 ^{ x}6 ^{ x}6, ПП187 <sup>ва

y</sup>ПП187 ^{ y}6 ^{ y}6, ПП187

Аниқланган координата қийматлари жадвални 13 ва 14 устунга йўл нуқталарига мос қаторига ѐзиб қўйилади.