Земля как космическое тело. Земля как космическое тело и ее внутреннее строение

• Название: Земля как космическое тело и ее внутреннее строение
• Анкор: Земля как космическое тело
• Дата: 20.10.2022
• Размер: 450 Kb.
• Имя файла: Земля как космическое тело.doc
• Тип: Документы; #743234

ЗЕМЛЯ КАК КОСМИЧЕСКОЕ ТЕЛО И ЕЕ ВНУТРЕННЕЕ СТРОЕНИЕ

Основные положения.

1. Земля - третья по расстоянию от Солнца большая планета Солнечной системы. Масса Земли равна 5976·10²¹ кг .Под действием притяжения Солнца Земля, как и др. тела Солнечной системы, обращается вокруг него по эллиптической (мало отличающейся от круговой) орбите. Большая полуось орбиты Земли, равная 149,6 млн. км, принимается за единицу при измерении расстояний в пределах Солнечной системы. Скорость движения Земли по орбите, равная в среднем 29,765 км/сек, колеблется от 30,27 км/сек (в перигелии) до 29,27 км/сек (в афелии). Вместе с Солнцем Земля участвует также в движении вокруг центра Галактики, период галактического обращения составляет около 200 млн. лет, средняя скорость движения 250 км/сек.

2 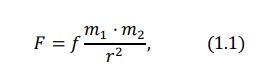. Гравитационное поле - это силовое поле, передающее взаимодействие масс. Сила гравитационного притяжения (F') определяется законом всемирного тяготения (И.Ньютон, 1686), и для двух материальных точек с массами m1 и m2, находящихся на расстоянии r, справедливо выражение: 𝐹

где f - гравитационная постоянная, согласующая размерности обеих частей уравнения. Она численно равна силе притяжения двух единичных масс, находящихся на расстоянии, равном единице. В системе СИ f = 6,67*10^-11 м³ /кг*с².

Именно гравитационное взаимодействие является причиной криволинейных движений космических тел: Луна вращается вокруг Земли, Земля и другие планеты - вокруг Солнца, Солнечная система - вокруг центра нашей галактики Млечного пути, Млечный путь - вокруг центра масс Вселенной.

Из законов Ньютона следует, что траектория движения тела m является кривой, лежащей в плоскости MmV0 а форма траектории определяется выражением, вытекающим из сохранения количества движения при взаимодействии: 𝑉



Если k< 1, т.е. гравитационное воздействие велико в сравнении с импульсом прямолинейного движения (большие массы, маленькое расстояние, низкая первоначальная скорость), то тело mупадёт на М . Если k = 1, то тело m движется по круговой орбите вокруг тела M. Если 1 2) траекториям.

3. Солнечная система.

Солнечная система включает в себя Солнце, 9 планет, поле астероидов и кометы. Остановимся на закономерностях движения планет. Кинематика движения описывается законами Кеплера (1609), причина движения - всемирное тяготение.

4. Все планеты обращаются по слабо вытянутым эллиптическим орбитам, в одном из фокусов которых находится Солнце. Орбиты лежат в одной плоскости - плоскости эклиптики. Вращение Солнца и планет вокруг своих осей, а также обращение планет вокруг Солнца происходит в одном направлении. Солнце расположено в одном из фокусов эллиптической орбиты Земли, вследствие чего расстояние между Землей и Солнцем в течение года меняется от 147,117 млн. км (в перигелии - ближайшая к Солнцу точка орбиты небесного тела, движущегося вокруг Солнца по одному из конических сечений - эллипсу, параболе или гиперболе) до 152,083 млн. км (в афелии - точка орбиты планеты, кометы или какого-либо другого тела, обращающегося вокруг Солнца, наиболее удалённая от Солнца). Вращение планет и Солнца происходит в таком направлении, что со стороны Северной Полярной звезды видится как вращение против часовой стрелки. В таком же направлении вращается Солнечная система вокруг центра галактики. Такое положение планет и Солнца определяет гравитационную устойчивость системы. Незначительные отклонения от общей закономерности вызваны взаимными гравитационными возмущениями планет. Так, наиболее отличается от эллиптической орбита Марса, вблизи которого вращается самая тяжёлая планета Солнечной системы - Юпитер. Радиус эклиптики (радиус орбиты) последней планеты равен 40 а.е. Астрономическая единица (а.е.) равна среднему удалению Земли от Солнца и составляет 149,6*10⁶ км.

5. Размеры орбит планет Солнечной системы не случайны, возрастают в геометрической прогрессии, квантованы и подчиняются закону Тициуса-Боде:



где аn - большая полуось орбиты в а.е.; n - целые числа в последовательности -0, 1 и т.д. Подставляя п в формулу 1.3, получаем оценочные размеры орбит в а.е.: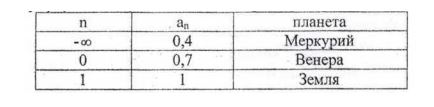



Согласно А.М. Молчанову, закон Тициуса-Боде отражает резонансность Солнечной системы, которая заключается не только в соразмерности планетных орбит, но и в согласованности периодов обращения по орбите и периодов вращения вокруг оси. Например, соединение Земли и Меркурия происходит каждые 116 суток, при этом Меркурий делает ровно 2 оборота вокруг оси и всегда повёрнут к Земле одной и той же стороной. Аналогичным образом ведёт себя другой «сосед» Земли - Венера. Одинаковое положение относительно Земли занимают самые большие планеты Юпитер и Сатурн через каждые 60 лет, за которые Юпитер делает 5 оборотов, а Сатурн - 2 (вспомним 12-летний и 60-летний циклы в китайском гороскопе). По Молчанову, 1) резонансность Солнечной системы является следствием и признаком её зрелости.

6. В каждый интервал времени произведение скорости планеты на расстояние до Солнца остаётся постоянным. Поскольку расстояние до Солнца изменяется, то изменяется и скорость движения Земли по орбите: максимальная скорость - в перигелии (30,27 км/с), минимальная - в афелии (29,27 км/с).

7. Массы планет, периоды их обращения по орбитам и размеры орбит взаимосвязаны. Соотношение между названными параметрами определяется третьим законом Кеплера, уточнённым после открытий Ньютона: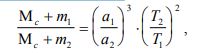



где Мс - масса Солнца, m1 и m2 - массы планет, а и Т - размеры орбит и периоды обращения планет по орбитам. Выражение 1.4 используется для вычисления масс планет, которые непосредственно из астрономических наблюдений определить невозможно.

8. Масса Земли составляет 6*10²⁴кг, её средний радиус - 6,4.10³ км, плотность вещества Земли (отношение массы к объёму) равна 5,52 г/см³ (более чем в пять раз плотнее воды). Соответствующие параметры для Солнца: Мс = 2*10³⁰кг, R = 7*10⁵ км,  = 1,4 г/см³.

9. Плотности вещества и массы планет Солнечной системы приведены на рис. 1.4. По этим параметрам все планеты делятся на две группы: планеты земной группы, характеризующиеся малыми массами и высокими плотностями, и внешние планеты с большими массами и низкими плотностями. Соответственно изменяется и состав планет: в планетах земной группы преобладают тяжёлые элементы (больше всего железа); состав внешних лёгких планет преимущественно гелиево-водородный.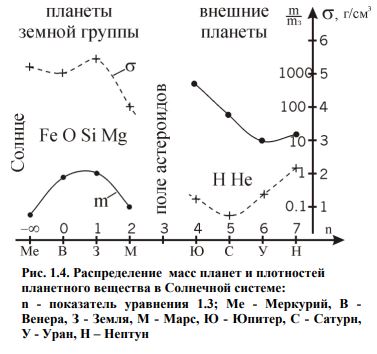



10. Наблюдаемое распределение состава и плотности планет обусловлено гравитационной дифференциацией вещества в поле притяжения Солнца, а также вытеснением лёгких газов солнечным давлением. В силу этой же причины среди планет земной группы наименьшие массы имеют крайние планеты - Меркурий и Марс, расположенные близко соответственно от Солнца и самой большой планеты Юпитер. Среди планет этой группы Земля находится на оптимальном расстоянии от Солнца и Юпитера, что позволяет ей иметь максимальную массу. Соответственно изменяется и состав планет: в планетах земной группы преобладают тяжёлые элементы (больше всего железа); состав внешних лёгких планет преимущественно гелиево-водородный. среди планет земной группы наименьшие массы имеют крайние планеты - Меркурий и Марс, расположенные близко соответственно от Солнца и самой большой планеты Юпитер. Среди планет этой группы Земля находится на оптимальном расстоянии от Солнца и Юпитера, что позволяет ей иметь максимальную массу.

11. Эволюция космических тел определяется массой, которую они приобрели при образовании. Сравним среднюю плотность Земли (5,52 г/см³ ) со средней плотностью горных пород вблизи её поверхности (2,7 г/см³ ) (рис. 2.5). Сравним также средний состав Земли (Fe-32%,О-30%, Si-15%, Mg- 14%) со средним составом земной коры (О-46,6%, Si-25.8%, Al-7,7%, Fe-6,6%). Такое сравнение должно привести к заключению, что Земля в настоящее время неоднородна (расслоена) и в центре Земли должно быть тяжёлое (преимущественно железное) ядро (рис. 2.5 и 2.6).Иначе не объяснить большие плотность и содержание тяжёлых элементов в Земле в целом, по сравнению с тем, что наблюдается в верхней её части. Химико-плотностная расслоенность космических тел является результатом их глобальной эволюции.

12. В качестве моделей строения Земли используются сферически симметричные физические модели распределения основных физических свойств: скоростей распространения продольных и поперечных волн, добротности среды, плотности, упругих модулей и некоторых производных характеристик. Рис. 1.4. Распределение масс планет и плотностей планетного вещества в Солнечной системе: n - показатель уравнения 1.3; Ме - Меркурий, В - Венера, З - Земля, М - Марс, Ю - Юпитер, С - Сатурн, У - Уран, Н – Нептун. В настоящее время широко используется параметрическая референтная модель Земли (PREM) А. Дзивонски и Д. Андерсона. Земля состоит из основных трех слоев: земная кора (слой А), мантия (верхняя В и С (иногда называют средней) и нижняя – слой D) и ядро (внешнее Е и внутреннее G, переходной слой между ними – F) - (рис. 1.5-1.8)







13. О расслоенности космических тел можно судить по измеряемому моменту инерции. Момент инерции является мерой инертности тела во вращательном движении и зависит от распределения в нём масс относительно оси вращения. Для сферы, коей можно аппроксимировать космические тела, момент инерции J равен:



где m - масса тела радиуса R; i - безразмерный момент инерции, определяющий распределение масс в сфере. Если i> 0,4, то массы сконцентрированы к периферии. Такое распределение масс крайне неустойчиво. Если i = 0,4, то массы распределены по сфере равномерно. При i< 0,4 массы сконцентрированы к центру, и тем больше, чем меньше значение i. Земля имеет i равный 0,33, что говорит о её расслоенности, о концентрации массы к центру (в ядре). Более это характерно для Солнца (i = 0,058), в центре которого плотность равна 160 г/см³ , при средней плотности 1,409 г/см³.

Слабо расслоенной является Луна (i=0,39). Причина расслоения - собственное гравитационное поле космического тела, что подтверждают данные, приведённые на рисунке 1.7: чем больше масса космического тела, тем больше у неё возможности к эволюции (гравитационной расслоенности).

ЗАДАЧИ.

1. Комета массой 10 кг движется прямолинейно со скоростью V0 в направлении, перпендикулярном относительно направления на Землю на расстоянии от неё r (рис. 1.1).

Какая то уж очень маленькая комета. 10 кг. Но раз в условии сказано 10кг, значит 10кг.



Дано:

V₀=12*10³м/с

r = 2,78*10⁶м

Решение:

П 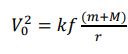рименим формулу

Имеем (V₀)²= 144*10⁶м²/с². f = 6,67*10-11 м³ /кг*с². Масса кометы 10кг пренебрежимо мала в сравнении с массой земного шара М=5,976*10²⁴кг.

Величину r примем как r из условия задачи плюс радиус Земли 6,37*10⁶м. Если r традиционно принять как расстояние между центрами масс тел, то комета окажется внутри земного шара.

Имеем r=9,15*10⁶м. Преобразуем формулу и найдём k.

k=(V₀)²*r/(M*f) = (144*10⁶м²/с²)*9,15*10⁶м/(5,976*10²⁴кг*6,67*10-11 м³ /кг*с²)=3,305.

Имеем k>2. Отсюда делаем вывод. Комета улетит от Земли по геоцентрической гиперболической траектории.

Увеличится ли вероятность падения кометы на Землю, если угол первоначальной траектории кометы с направлением на Землю будет острым?

Угол траектории должен быть таким, чтобы гипербола пересекла поверхность Земли.



Какие ещё параметры кометы должны измениться (и как), чтобы падение на Землю было возможно.

Если параметр k сделать меньше единицы, то столкновение возможно. Массаи радиус Земли изменению не подлежат. Гравитационная постоянная тоже. А скорость кометы уменьшить можно. Если V₀ уменьшить в 1,82 раза - (корень квадратный из 3,305), то столкновение возможно.

Задача 2.

Оцените скорость движения Земли на орбите в точке, удалённой от Солнца на расстоянии r а.е., если при среднем удалении от Солнца в 1 а.е. (149,6*10⁶ км) её средняя скорость составляет 29,8 км/с? Для нас это зимнее или летнее время года?

Дано:

r=151*10⁶км.

Решение:

Согласно правилу

В каждый интервал времени произведение скорости планеты на расстояние до Солнца остаётся постоянным.

Находим.

V*r=V₀*r₀

Отсюда v=149,6*29,8/151=29,52км/с.

Афелий орбиты Земля проходит 4 июля. Для нас это лето.

3. Приближённо оцените период обращения планеты по орбите, используя закон Кеплера-Ньютона (1.4) и закон Тициуса-Боде (1.3)

Закон Кеплера-Ньютона.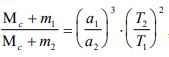



Закон Тициуса-Боде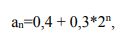



Таблица периодов обращения планет в отдельном файле.

4. Оцените среднюю плотность слоев Земли: 1) земной коры, 2) мантии и 3) ядра. Сравните со средней плотностью вещества Земли. Плотностям каких минералов они соответствуют? Предложите состав ядра. Ваш сравнительный прогноз о градиенте изменении плотности с глубиной планет с разными массами: Меркурий, Земля, Юпитер.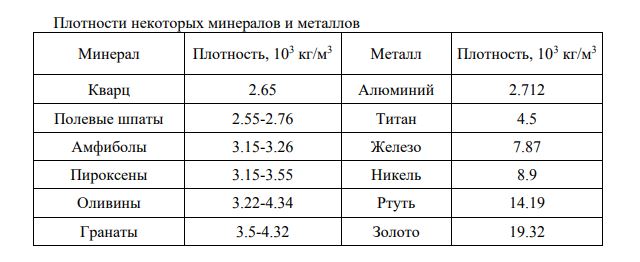





Решение:

Применим формулы для земного ядра.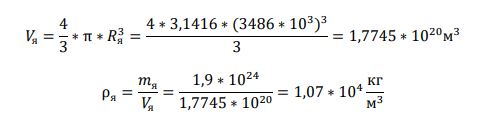



Аналогично для мантии Земли.

Vm=(4/3)*π*((Rm)³-(R_я)³)=4*3,1316*((6353*10³)³-(3486*10³)³)/3=8,966*10²⁰м³.

ρм=m_м/Vm=4,1*10²⁴/(8,966*10²⁰)=4572кг/м³.

Для земной коры

Vк=(4/3)*π*((Rк)³-(Rм)³)=4*3,1316*((6371*10³)³-(6353*10³)³)/3=9,155*10¹⁸м³.

ρк=m_м/Vm=2,4*10²²/(9,155*10¹⁸)=2621кг/м³.

Можно предположить, что ядро состоит из железа и никеля с возможными примесями тяжелых элементов. Мантия по плотности похожа на титан. Земная кора - кварц, полевой шпат.

Ваш сравнительный прогноз о градиенте изменении плотности с глубиной планет с разными массами: Меркурий, Земля, Юпитер.

Меркурий имеет плотность 5450 кг/м3. Можно предположить наличие большого железного ядра.

Земля сильно дифференцирована по плотности. У неё есть кора из легких пород. Можно предположить наличие крупного железного ядра.

Юпитер должен быть сильно дифференцирован. Он имеет протяженную водородную атмосферу. Судя по моменту инерции 0,2, Юпитер должен быть сильно дифференцирован. Можно предположить наличие силикатного или железного ядра.