Знаменитые задачи древности: удвоение куба. реферат вммм. Знаменитые задачи древности удвоение куба
 Скачать 5.79 Mb.
|
1 2 Возможно, в связи с тем, что задача об удвоении куба продолжала привлекать к себе внимание ученых, а решение ее Архитом представлялось им сложным, в Древней Греции продолжались поиски новых методов построения средних пропорциональных для двух данных отрезков. В 4 в. до н.э. известными учеными Древней Греции, занимавшимися решением делосской задачи, были Евдокс и Менехм. 2 Первое решение Менехма Что касается Менхема, то Евтокий в своих комментариях приводит два его решения. Рассмотрим первое: «Пусть две заданные прямые  будут перпендикулярны друг другу. Пусть для них средние пропорциональные будут , так что: . Проведем перпендикуляры , так как , то точка  находится на параболе с осью . Затем так как  то прямоугольник между , т.е. другой заданной линией и будет равен квадрату на или на ∆Z, т.е.  2, Значит Z находится на параболе с осью ∆В.Но она находится и на другой параболе с осью ВЕ, значит точка известна. Затем, так как ∆Z и ZE перпендикулярны, то будут известны и точки ∆ и Е. Построение производится так: пусть две заданные прямые АВ и ВГ будут взаимно перпендикулярны, продолжим их из В до бесконечности. На оси ВЕ построим параболу так, чтобы ее опущенные на ВЕ ординаты квадрировались на АВ (т.е.  Обе эти параболы пересекут друг друга в точке Z. Проведем из Z перпендикуляры Z∆ и ZЕ. Так как в одной параболе проведена ордината ZЕ, т.е. ∆В, то значит прямоугольник между ГВ и ВЕ равен квадрату на B∆, т.е.  , и поэтому ГВ относится к B∆ как ∆В к ВЕ. Но ∆В относится к ВЕ как ГВ к ВА и, следовательно, ГВ относится к B∆ как ∆В к ВЕ и как ВЕ к ВА, т.е.  , что и требовалось получить.Следовательно, в данном решении используются две параболы. Если перевести эту задачу на язык аналитической геометрии, то дело сводится к нахождению абсциссы точки пересечения двух парабол, уравнения которых  Из второго уравнения следует, что у=х2/a2,подставляем в первое и получаем x4/a2=2ax или х3=2а3 и х = а  . Таким образом, искомое ребро куба есть абсцисса точки пересечения двух парабол.2 Второе решение Менехма 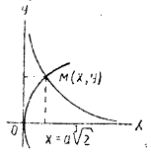 Аналогично первому, но в этом случае он использует параболу и гиперболу, уравнения которых получаются тоже из равенства  . Только в первом случае он рассматривал уравнения  , откуда и получились уравнения х2 = 2ау и у2 = 2ах. Во втором случае надо рассматривать равенства  и  . Отсюда получаются уравнения параболы  и гиперболы ху = 2а2. Чтобы определить теперь искомую величину х, нужно найти точку пересечения этих кривых, абсцисса х = а .Так как из второго уравнения выражаем  , подставим в первое уравнение и получим 4а4/x2 = 2ax, откуда 4а4 = 2ах3, и х3 = 2а3, следовательно, х = а .Таково решение этой задачи Менехмом. 3 Решение Эратосфена 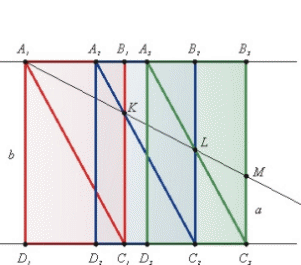 Эратосфен Киренский придумал механический прибор для решения задачи. Он состоит из трех одинаковых прямоугольников A1B1C1D1, A2B2C2D2 и A3B3C3D3, на которых нaрисовaны диaгонaли A1C1, A2C2 и A3C3. Противоположные стороны прямоугольников (A1B1 и C1D1, A2B2 и C2D2, A3B3 и C3D3) могут свободно двигаться по двум пaрaллельным прямым. Пусть расстояние между прямыми равно b, а на стороне B3C3 отмечена точка M тaкaя, что C3M = а. Будем двигать второй прямоугольник так, чтобы точка A2 не выходила за пределы первого прямоугольника, а второй - так, чтобы точка A3 не выходила за пределы второго. Тогда при движении второго прямоугольника точка пересечения прямых A2C2 и B1C1 (обозначим эту точку K) будет проходить отрезок B1C1. Назовем L точку пересечения прямых A3C3 и B2C2. Если прямоугольники находятся в таком положении, что точки A1, K, L и M все лежат на одной прямой, треугольники A1KC1, KLC2 и LMC3 подобны между собой, также как и треугольники A1C1D1, KC2C1 и LC3C2, и трапеции A1KC1D1, KLC2C1 и LMC3C2, и поэтому задача удвоение куб  . Таким образом, и если  , то LC2=а .Хотя, как вы можете непосредственно убедиться, этот метод не очень удобен - хлопотно проверять, что A1, K, L и M лежат на одной прямой - сам Эратосфен гордился им и сочинил эпиграмму. «Если из малого куба двойной замышляешь устроить, Друг, или данный объем к форме другой привести, Чтоб хорошо удалось тебе это, вздумал ли погреб Ты измерять, или ров, или широкую пасть Глуби колодца, возьми на смежных концами плaстинкaх Средние линии две, сжатые между таблиц. Не прибегай для этого ты к тяжелым цилиндрам Aрхитa,онусa ты не секи, корня Mенехмa триад; Также не надо держать с богоравным евдоксом совета, Выгнутых линий его формы не надо чертить.этими ж ты тaбличкaми тысячи средних построишь, Двигайся смело вперед, с меньших из данных нaчaв. Пусть же свершится все это, и каждый смотрящий пусть скажет: «Это Kирены сын выдумал Эратосфен». Об упомянутом решении Евдоксa почти ничего не известно. B приведенной эпиграмме справедливо отмечено, что методом Эрaтосфенa, в сущности, можно построить не только два, но и сколько угодно средних пропорциональных между двумя данными отрезками при достаточном числе «табличек». Заключение Таким образом, мы рассмотрели несколько видов решения одной из пяти знаменитых задач древности. Вышеперечисленными решениями задачи удвоения куба история далеко не исчерпывается, но мы разобрали самые известные из них. Список литературы 1)Белозёров С.Е. «Пять знаменитых задач древности» )История математики (Удвоение куба и трисекция угла): http://sc.nios.ru/dlrstore/bb92a95d-5d2d-ce45-7289-11f4524d621e/00145619786669533.htm 1 2 |