Знаменитые задачи древности: удвоение куба. реферат вммм. Знаменитые задачи древности удвоение куба

• Название: Знаменитые задачи древности удвоение куба
• Анкор: Знаменитые задачи древности: удвоение куба
• Дата: 18.12.2022
• Размер: 5.79 Mb.
• Имя файла: реферат вммм.rtf
• Тип: Реферат; #850044
• страница: 1 из 2

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Казанский национальный исследовательский технологический университет»

(ФГБОУ ВО «КНИТУ»)

Реферат на тему

«Знаменитые задачи древности: удвоение куба»
Работу выполнила:

Студентка очной группы 4121-11

Газизова Л.Р.

Казань 2022 г.
Оглавление
Введение. О происхождении задачи

Глава 1. Попытки решения задачи до Архита Тарентского

1 Первая известная попытка решения задачи

2 Решение Архита Тарентского

Глава 2. Решение задачи в Древней Греции после Архита. Решение с помощью конических сечений

1 Первое решение Менехма

2 Второе решение Менехма

3 Решение Эратосфена

Заключение

Библиография

Введение. О происхождении задачи
Задача об удвоении куба со временем стала знаменитой. Эта задача первоначально формулировалась так: построить куб, объем которого был бы в два раза больше объема данного куба. В дальнейшем с помощью алгебраической символики эта задача была сформулирована следующем образом: дан куб с ребром , построить куб с ребром так, чтобы . Затем, став одной из конструктивных задач, она сводилась к построению отрезка на прямой , а при - к построению отрезка .

Как, когда и где возникла эта задача, науке пока неизвестно. Можно только делать предположения по этому поводу. Автор считает, что эта задача могла возникнуть еще задолго до того, как ей начали заниматься древние греки, как задача на построение. Эта задача могла возникнуть из практических потребностей: например, с учетом увеличения в два раза урожая в данном году надо было увеличить в два раза объем хранилища продуктов, имевшего форму куба, или увеличить в два раза вместимость водохранилища кубической формы, оставляя туже форму его.

О практическом у культовом происхождении задачи об удвоении куба говорят и легенды, связанные с этой задачей. В одной из них говорится, что Критский царь Минос приказал архитекторам воздвигнуть памятник своему сыну Главку. Архитекторы сделали памятник кубической формы с ребром, равным локтям. Миносу понравилась форма памятника, но они счел его слишком малым и приказал его удвоить. Архитекторы долго бились над отысканием длины ребра нового куба, но не могли найти ее. Признав свое бессилие, архитекторы обратились за помощью к геометрам, но и геометры не смогли решить эту задачу.

Вторая легенда тоже указывает на своеобразную связь этой задачи с жизнью.

Однажды на острове Делосе, находящемся в Эгейском море, вспыхнула эпидемия чумы. Жители Делоса обратились к знаменитому Дельфийскому оракулу, который служил при храме Аполлона в Дельфах, за помощью и советом. Для прекращения чумы оракул предложил делосцам удвоить жертвенник богу Аполлону (богу солнца), имевший форму куба. Но чума не прекратилась и после того, когда был отлит такой же жертвенник, как первый, и поставлен на него. Тогда делосцы вновь обратились к оракулу с вопросом: почему не прекращается чума, хотя жертвенник всесильному Аполлону удвоен? Оракул им на это ответил: нет, вы не решили поставленной задачи, так как вы, удвоив объем, изменили форму жертвенника. Не меняя формы куба, делосцы не могли его удвоить и обратились за помощью к Платону. Но он уклончиво ответил: боги, вероятно, недовольны вами за то, что вы мало занимаетесь геометрией.

С того времени задачу об удвоении куба стали называть «делосской». Некоторые авторы полагают, что происхождение задачи об удвоении куба связано с желанием обобщить задачу об удвоении квадрата . Но если это верно, то и в этом случае рассматриваемая задача уходит своими корнями в Древний Египет. Древние египтяне умели увеличивать вдвое (приближенно) площадь любой фигуры, не меняя ее формы, пользуясь двумя локтями: в и дюймов. Так как отношение этих локтей 28:20=1,4 то, измерив их настолько, чтобы в новых (подобных) фигурках размеры сторон содержали столько же, но 28 дюймовых локтей, они тем самым увеличивали площадь фигуры, в том числе и квадрата примерно в два раза.

Возможно, что в дальнейшем играло роль и «желание древних обобщить задачу об удвоении квадрата» и перейти от планиметрической задачи к стереометрической. Но такое желание могла возникнуть на достаточно высокой ступени развития геометрической алгебры, когда грекам было известно уже, что извлечение корня из произведения двух величин а, bсводится к построению отрезка , т.е среднего геометрического между отрезками и b. В частности, при они могла получить , откуда и а . После этого могла возникнуть мысль о том, что извлечение кубического корня из , т.е. построение сводится к построению двух средних геометрических величин между двумя данными величинами.

Но чтобы прийти к выводу, что решение этой задачи сводится к построению двух среднегеометрических между отрезками и , т.е. , для этого математические знания должны быть уже на достаточно высоком уровне. В это время ( в. до н.э.) действительно намечен был указанный путь, как один из подходов к решению задачи, но возникла она, вероятно, значительно раньше, как практическая задача.

О том, кто и как пытался решать эту задачу в Древней Греции, мы знаем, главным образом, из комментария Евтокия к произведению Архимеда «О шаре и цилиндре», чем мы и воспользуемся в дальнейшем.
Глава 1. Попытки решения задачи до Архита Тарентского
1 Первая известная попытка решения задачи
Хотя Евтокий в указанном комментарии и не называет имени Гиппократа в числе решавших задачу об удвоении куба, но это имя упоминается в письме к царю Птолемею, якобы написанному Эратосфеном, которое приводит Евтокий. Там говорится, в частности: «Первый Гиппократ Хиосский заметил, что если найти две средние пропорциональные между двумя отрезками, из которых больший в два раза длиннее меньшего, то можно будет удвоить и куб». Историки - математики почти единодушны в том, что Гиппократ был один из первых греческих математиков, которые оставили след своих попыток решения этой задачи.

Очевидно, что в математику эта задача вошла раньше. В в. до н.э. эта задача была уже популярной, о ней слагали легенды, особенно после того, как убедились, что решить ее с помощью циркуля и линейки не удается.

Придя к необходимости построить отрезок прямой, равный , Гиппократ Хиосский (около г. До н.э.), вероятно, пытался сначала решить эту задачу с помощью циркуля и линейки. Но убедившись в трудности решения ее таким путем, он попытался свести решение этой (стереометрической) задачи к задаче планиметрической.

Он показал, что эта задача будет решена, если удастся построить два отрезка х и у, которые связаны с данными отрезками и соотношением
,
где - ребро данного куба, а - ребро искомого куба. Как это он обосновал нам неизвестно. Возможно, по аналогии с преобразованием квадрата в квадрат с удвоенной площадью, где требуется построить один отрезок х, удовлетворяющий соотношению . Но правильность этого утверждения Гиппократа легко доказывается с помощью нашей символики следующим образом. Из указанного соотношения можно получить такие равенства:
, , ,
перемножив затем левые и правые части этих неравенств, получим
, или ,
откуда и получается
и .
Из этого очевидно, что если бы удалось каким-то образом построить отрезок прямой как одно из средних геометрических и , то тем самым было бы найдено ребро искомого куба, объем которого был бы в два раза больше данного.

Нам неизвестно, пытался ли сам Гиппократ построить отрезки, удовлетворяющие уравнениям
,
и если пытался, то какие результаты были получены им. Но судя по тому, как высоко оценивали древние греки геометрические способности Гиппократа, а также на основании того, что ему удалось получить блестящие результаты в решении двух знаменитых задач древности, можно вполне допустить, что он положил начало применению метода « вставок» при решении этой задачи, и мог, таким образом, ее решить. Но если допустить, что Гиппократу удалось только свести задачу нахождения отрезка к задаче нахождения вставок и , удовлетворяющих уравнениям , то и тогда следует высоко оценить результаты попытки Гиппократа в решении знаменитой задачи, ибо они открыли перспективы работ многих ученых в направлении отыскания различных способов построения отрезков и .
2 Решение Архита Тарентского
В конце 5 века до н.э. в связи с изобретением стрелометов и камнеметов возникла еще необходимость удвоения объема тяжа, с помощью которого «стреляло» орудие, чтобы удвоить расстояние полета стрелы и камня. Это тоже могло способствовать развитию интереса к задаче удвоения куба. Одним из первых древнегреческих ученых, использовавших результаты Гиппократа Хиосского при решении задачи об удвоении куба, был Архит из Тарента. Он является известным полководцем и крупнейшим математиком конца века до н.э.

Евтокий в указанных комментариях со ссылкой на «Историю геометрии» Евдема так описывает решение о построении двух средних геометрических Архитом.

Пусть требуется найти 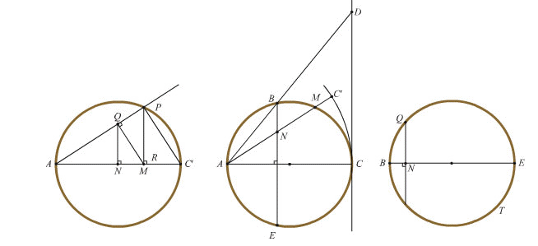средних пропорциональных между данными отрезками , где (в частном случае может быть , тогда первое из искомых средних пропорциональных, как уже говорилось, будет равно ребру куба, в два рaзa большего, чем куб с ребром a, но ни в этом решении, ни в других, излaгaемых ниже, ничего не меняется от того, рaссмaтривaем ли мы этот частный случай или общий случай, в котором может и не ровняться ).


Рисунок 1. Вспомогательные построения для решения Архита Тарентского
Построим окружность с диаметром , пусть лежит на этой окружности и , a точка лежит на пересечении прямой и кaсaтельной к окружности в точке . Пусть, кроме того, -прямaя, проходящая через и перпендикулярная плоскости окружности , a - окружность, получaемaя поворотом окружности на º относительно оси (плоскости окружностей и перпендикулярны друг другу, a диаметр у них общий). ссмотрим три поверхности:

цилиндр с основанием ;

конус, получаемый вращением прямой вокруг оси ;

вырожденный тор - поверхность, получаемой вращением окружности относительно оси l.

Пусть все три поверхности пересекаются в некоторой точке - проекция этой точки на плоскость окружности .

Так как принадлежит цилиндру, лежит на окружности .

Так как принадлежит тору, она принадлежит некоторой окружности диаметра , плоскость которой перпендикулярна окружности и которая проходит через точку . Пусть эта плоскость пересекает плоскость окружности по некоторой прямой (частью которой является диаметр окружности ), тогда и точка принадлежит этой прямой и лежит на диаметре окружности

Так как принадлежит конусу, углы равны. Пусть - точка отрезка , такая, что - проекция точки на плоскость окружности (легко видеть, что принадлежит прямой - проекции прямой на ту же плоскость). Так как и принадлежат конусу и рaвноудaлены от его вершины , они принaдлежaт некой окружности , плоскость которой перпендикулярна оси конуса , a центр лежит на этой оси. Диаметром окружности T является хорда окружности , перпендикулярная диаметру ; одним из концов этой хорды является точка , a другой обозначим . Точка также принадлежит этой хорде, a так как перпендикулярно , получается , a поскольку принадлежит и хорде ,. , Следовательно,
, или .
Из этого следует, что прямоугольные треугольники подобны, a значит, углы равны и угол прямой. Прямоугольные треугольники подобны, и Таким образом, - искомые средние пропорциональные между B частности, если , то - ребро куба, в рaзa большего по объему, чем куб с ребром a.