Конспект ряд Тейлора. ряд тейлора. Разложение функции в степенной ряд

• Название: ряд тейлора. Разложение функции в степенной ряд
• Анкор: Конспект ряд Тейлора
• Дата: 03.05.2023
• Размер: 313 Kb.
• Имя файла: п_3.doc
• Тип: Документы; #1104786

§ 3. РЯД ТЕЙЛОРА
. Разложение функции в степенной ряд

Всякая функция, бесконечно дифференцируемая в интервале 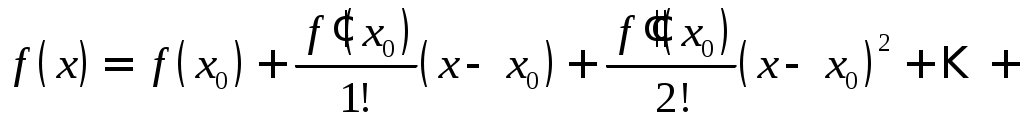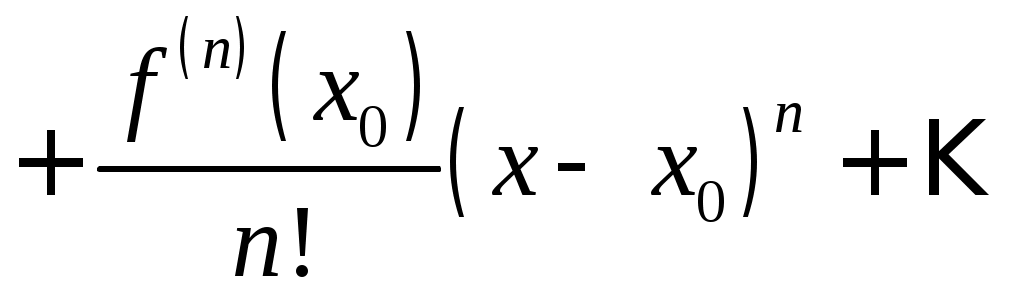, т.е. , может быть разложена в этом интервале в сходящийся к ней степенной ряд Тейлора

, (1)
если в этом интервале выполняется условие

,

где – остаточный член формулы Тейлора (или остаток ряда), .

При получается ряд Маклорена:

.

Если в некотором интервале, содержащем точку , при любом выполняется неравенство , где – положительная постоянная, то и функция разложима в ряд Тейлора.

Для оценки остаточного члена можно пользоваться формулой

где (2)

(форма Лагранжа).

Пример 1. Разложить функцию в ряд по степеням .

Решение. Находим производные данной функции : , , вообще , если – четное и , если – нечетное. Полагая , получим, , , , , вообще , если

– четное, и , если – нечетное. Отсюда на основании (1) имеем:

(3)

Для определения интервала сходимости ряда (3) применяем признак Даламбера.

Имеем:



при любом 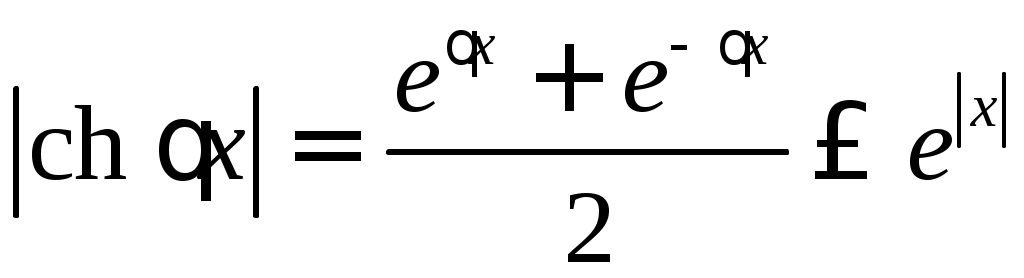. Следовательно, ряд сходится в интервале . Остаточный член в соответствии с формулой (2) имеет вид

, если нечетное , и

, если четное.

Так как , то

,

,

и потому . Ряд с общим членом сходится при любом (в этом можно легко убедиться с помощью признака Даламбера), поскольку в соответствии с необходимым признаком сходимости

,

а следовательно, и при любом . Это означает что сумма ряда (3) для любого действительно равна .


. Приемы, применяемые при разложении в степенные

ряды

Пользуясь основными разложениями

1. 
   ,
   
2. 
   ,
   
3. 
   ,
   
4. 
   ; на границах интервала сходимости это последнее разложение имеет место:
   

при , если ,

при , если ,

при , если .

5. 
   ;
   
6. 
   ;
   
7. 
   ;
   

можно во многих случаях просто получать разложение данной функции в степенной ряд, причем отпадает необходимость исследования остаточного члена. Иногда при разложении полезно использовать почленное дифференцирование или интегрирование. При разложении в степенные ряды рациональных функций рекомендуется разлагать эти функции на простейшие дроби.

Пример 2. Разложить по целым и положительным степеням функцию .

Решение. Разложив функцию на простейшие дроби, будем иметь:

.

Так как

(4)

и

, (5)

то окончательно

(6)

Геометрические прогрессии (4) и (5) сходятся соответственно при и следовательно, формула (6) справедлива при , т.е. при .

Пример 3. Разложить в ряд по степеням функцию

.

Решение. Продифференцируем функцию 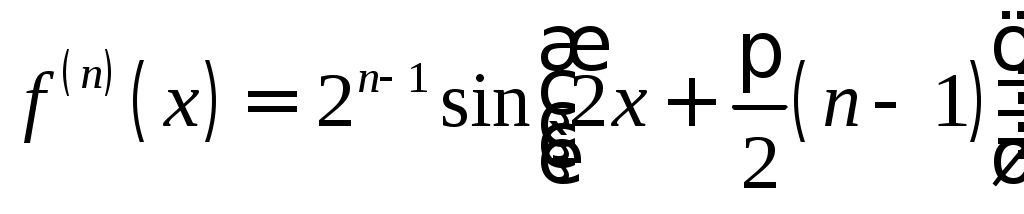раз:

,

,

,

,

,

,

,

.

Находим значение функций , , ,…, в точке , а значение определяем в точке (см. равенство для определения ). Получаем , , , , , , , …, .

Находим остаточный член: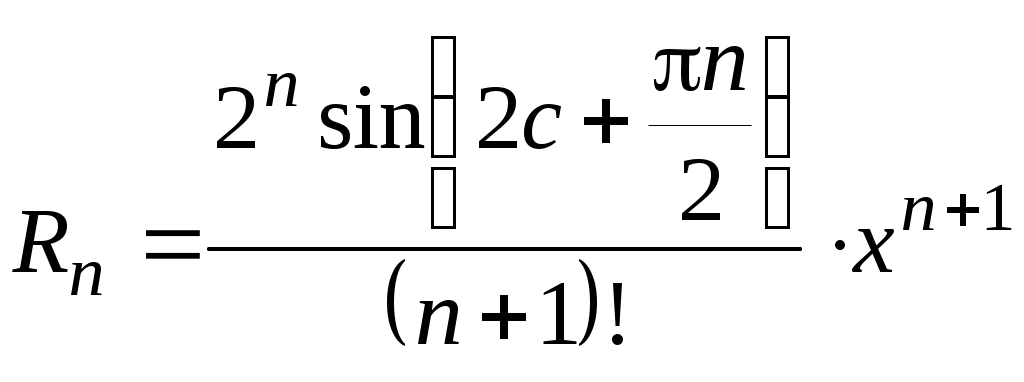

,

т.е.

.

Так как при любом , а – величина ограниченная, то . Следовательно, функцию можно представить в виде суммы ряда Маклорена

.

Задачу можно решить и иначе. В равенстве заменим его разложением в степенной ряд:

.

Выполнив несложные преобразования, получим найденное выше разложение .

Пример 4. Разложить в ряд по степеням .

Решение. В разложении



заменим на ; получим

.

Пример 5. Разложить в ряд по степеням .

Решение. В разложении



заменим на ; получим

.

Пример 6. Разложить в ряд по степеням .

Решение. Воспользуемся равенством 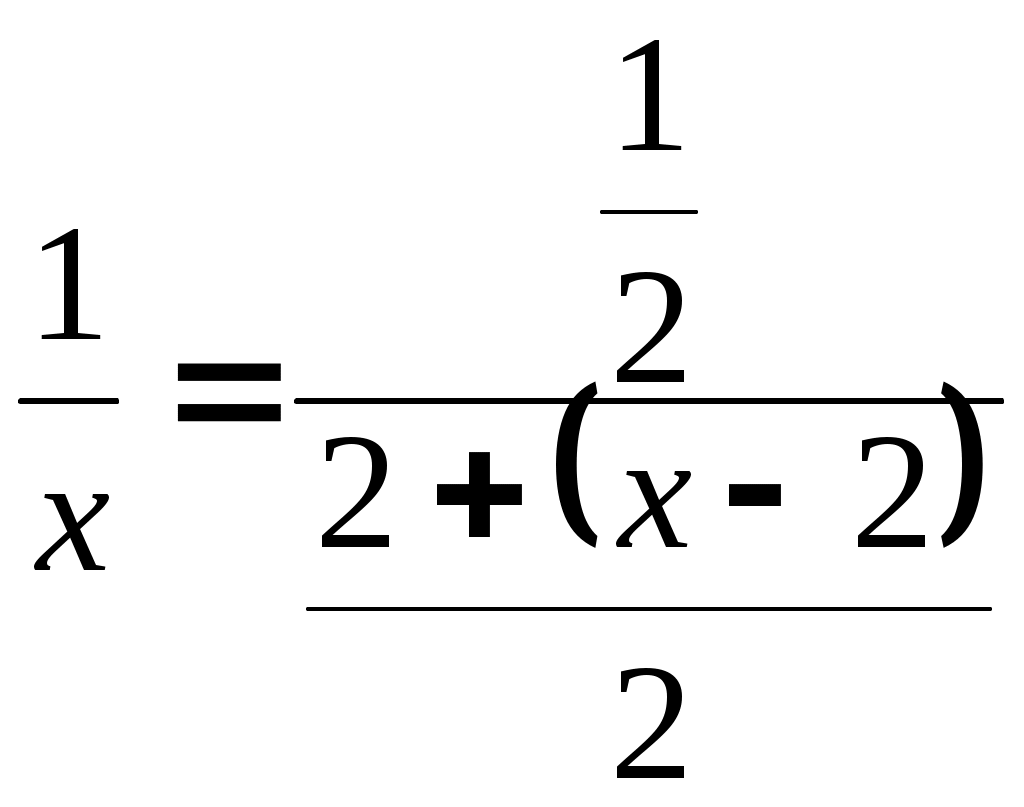. Правую часть этого равенства можно рассматривать как сумму бесконечно убывающей геометрической прогрессии с первым членом и знаменателем . Отсюда получаем

,

т.е.

.

Так как , то .

Пример 7. Разложить в ряд по степеням функцию .

Решение. Найдем значения функции и ее производных при :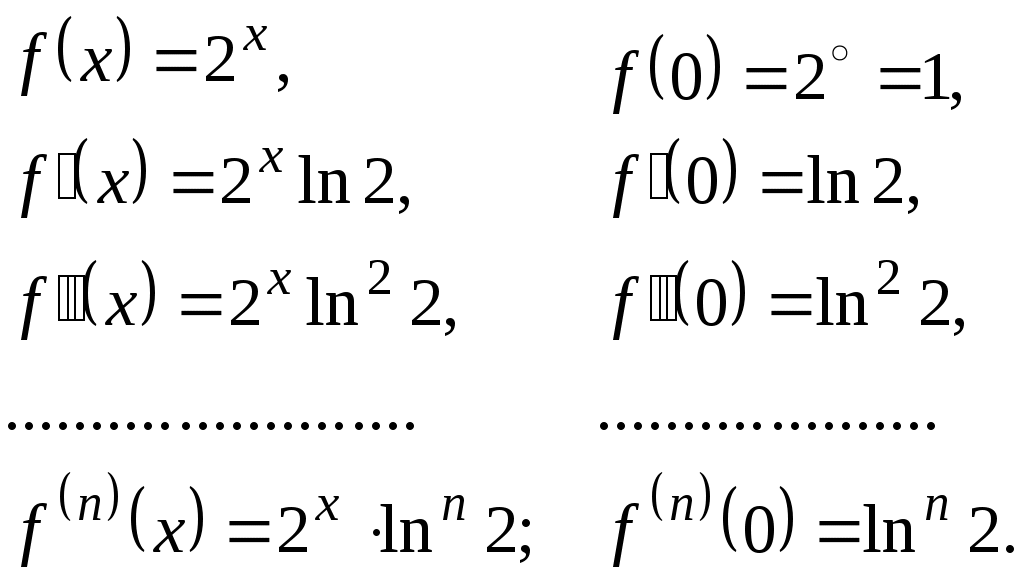



Так как , то при фиксированном имеет место неравенство для любого . Следовательно, функция может быть представлена в виде суммы ряда Маклорена:

.

В данном случае

.

Это разложение можно получить и иначе: достаточно в разложении



заменить на , так как

,

тогда

, при

.