Кинематика вращательного движения. 1. Краткое теоретическое содержание
 Скачать 292.5 Kb. Скачать 292.5 Kb.
|
|
1. Краткое теоретическое содержание: 1. Явление: вращение тела относительно неподвижной оси. 2. Определения основных физических понятий, процессов и величин: Твердое тело - система материальных точек, взаимное расположение которых не будет меняться ни при каких обстоятельствах. Любое сложное движение твердого тела можно представить, как комбинацию поступательного и вращательного движения. Поступательное движение - движение, при котором любая прямая, мысленно проведенная в теле, остается постоянной самой себе в течение всего времени движения. При поступательном движении траектории всех точек тела одинаковы, скорости и ускорения всех точек в данный момент времени равны. Поэтому можно описывать движение одной точки. Вращательное движение - движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения, а плоскости перпендикулярны к ней. Ось неподвижна. Положение тела в пространстве полностью определяется значением угла поворота φ тела из некоторого начального положения. Для характеристики быстроты и направления вращения тела вокруг оси служит угловая скорость – вектор 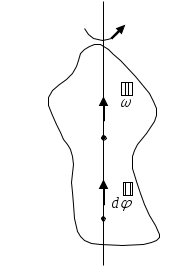 , ,где dφ – вектор элементарного (малого) поворота тела за время dt, направленный вдоль оси вращения по правилу винта. (Векторы dφ и Произвольная точка вращается вокруг неподвижной оси. Линейная скорость v связана с угловой скоростью ω соотношением: Модуль линейной скорости Она направлена перпендикулярно оси вращения и радиус-вектору Для характеристики быстроты изменения вектора угловой скорости при неравномерном вращении тела вокруг неподвижной оси (точки) вводится вектор 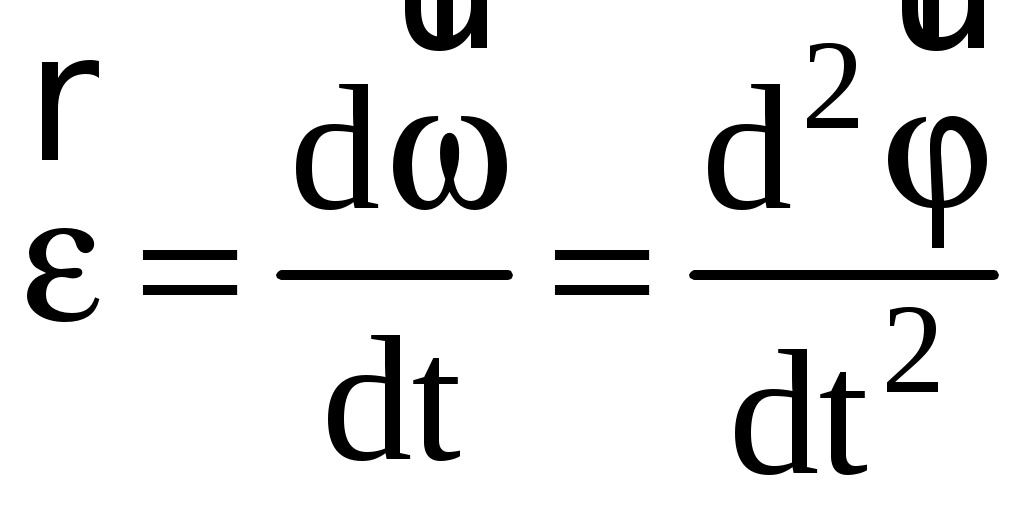 . .Если Если 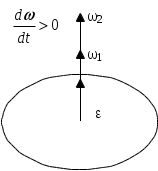 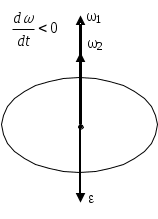 Тангенциальная составляющая ускорения 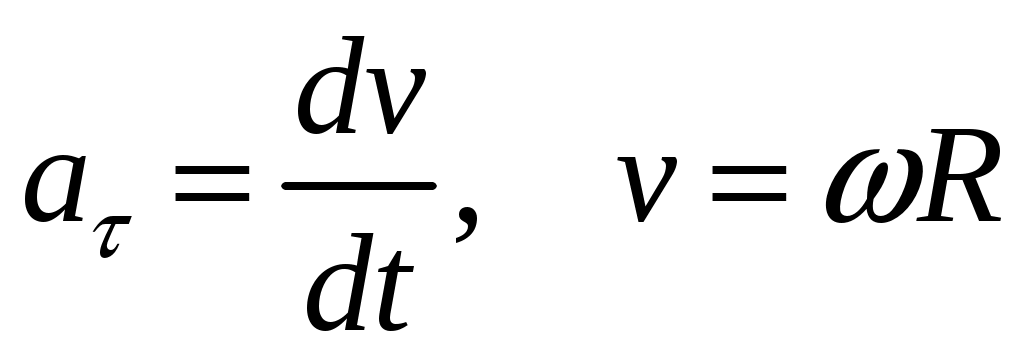 и 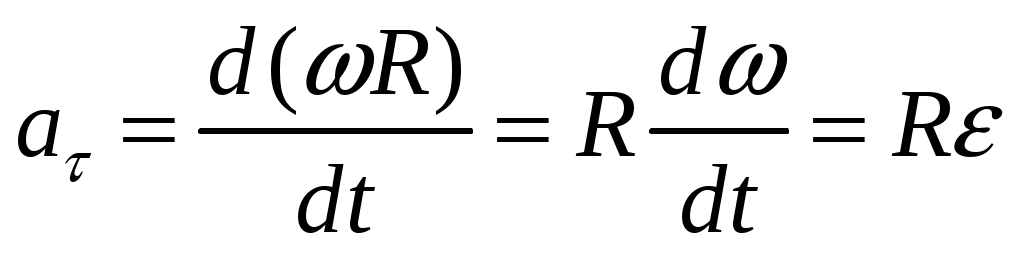 . .Нормальная составляющая ускорения 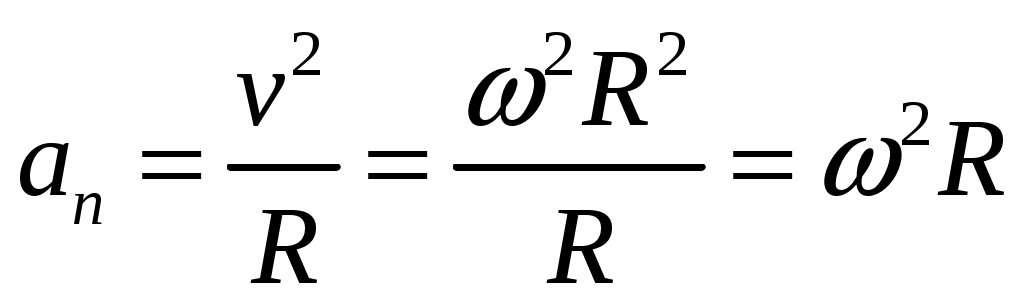 . .2. Задание: Сплошной диск вращается относительно оси, проходящей через его центр масс и перпендикулярной плоскости диска. Угол поворота со временем изменяется по закону Значения коэффициентов в уравнениях: B=0,1 Построить: графики изменения со временем угла поворота Определить: для точки, находящейся на расстояние R=0,16 м от оси, полное ускорение и число оборотов N, сделанных диском в момент времени t=5 c. 3. Решение 1) Уравнение изменения со временем угла поворота: 2) Уравнение изменения со временем угловой скорости: Угловая скорость – вектор 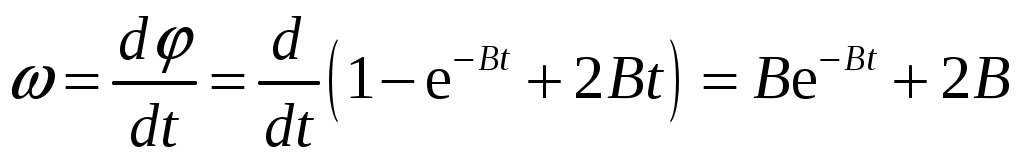 3) Уравнение изменения со временем углового ускорения: Угловое ускорение тела, равно первой производной от его угловой скорости 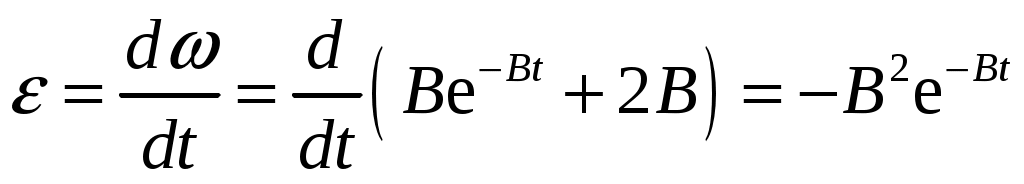 . .Задание 2 Модуль полного ускорения вычисляется по формуле: где Тогда 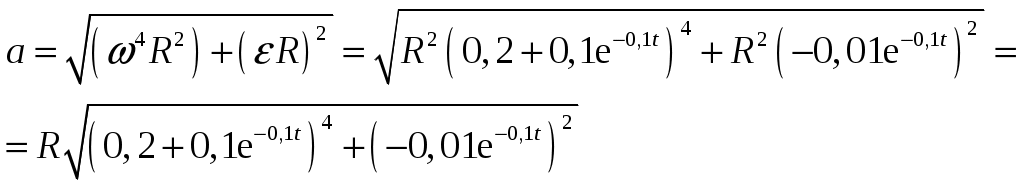 Число оборотов N, сделанных диском в момент времени t. Т.к. Отсюда 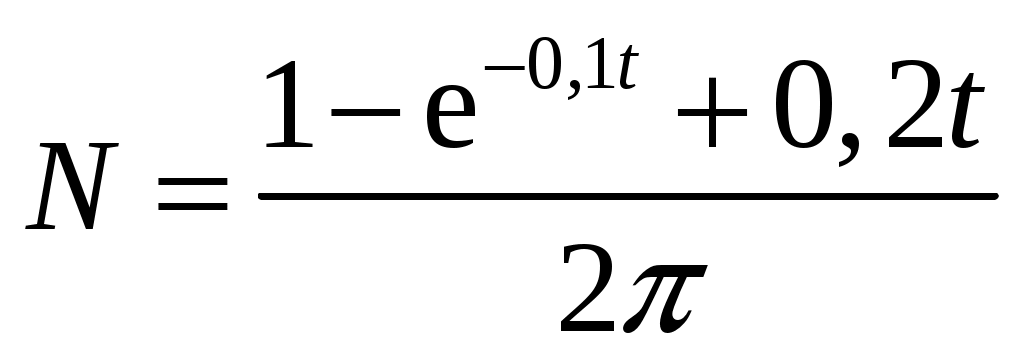 . .Проверка размерности величин: Расчет результатов: 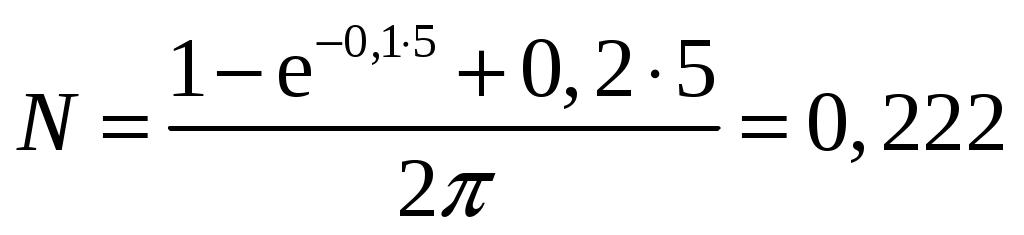 Графический материал: 1)Данные для графика изменения со временем угла поворота: Аналитическое выражение: График изменения со временем угла поворота: 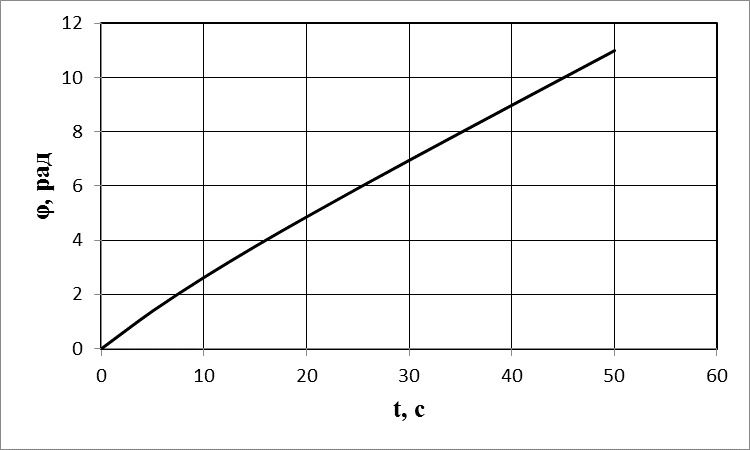
2) Данные для графика изменения со временем угловой скорости: Аналитическое выражение: График изменения со временем угловой скорости: 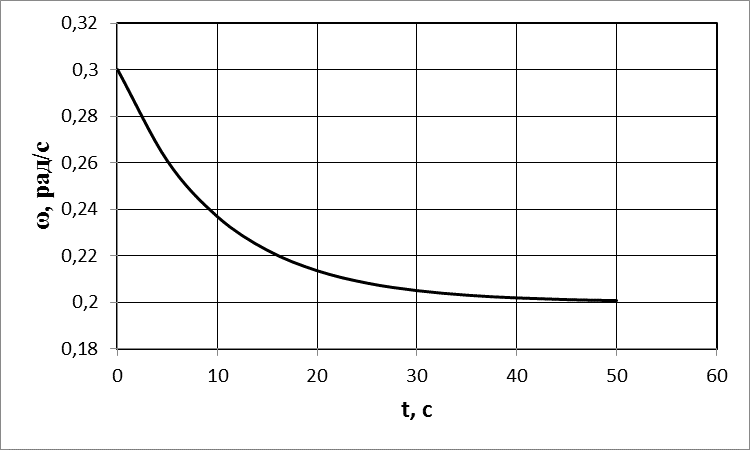
3) Данные для графика изменения со временем углового ускорения: Аналитическое выражение: График изменения со временем углового ускорения: 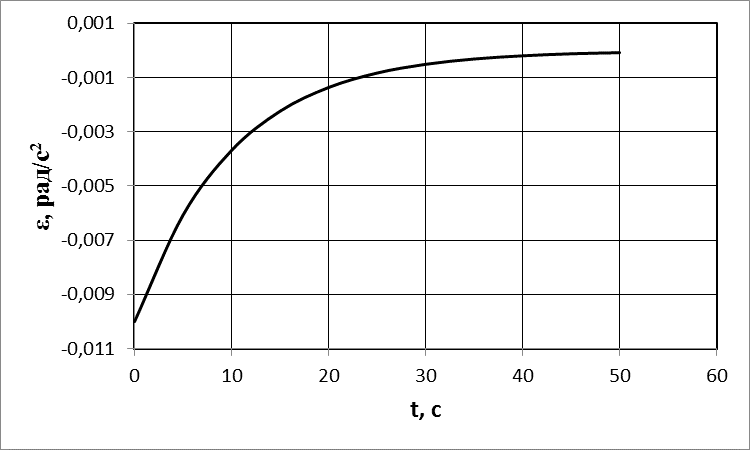
Анализ полученных результатов: в результате произведенных вычислений были: получены уравнения изменения со временем угла поворота, угловой скорости и углового ускорения; построены графики изменения со временем угла поворота |
