1. Матрицы (основ .понятия, виды, действия над матрицами)
Определение Матрице – называется таблица чисел содержащая определенное количество строк и столбцов
Элементами матрицы являются числа вида aij , где i- номер строки j- номер столбца.
Виды матриц:
1. Если число строк не равно числу столбцов 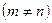 , то матрица называется прямоугольной: , то матрица называется прямоугольной:
Если число строк равно числу столбцов  , то матрица называется квадратной: , то матрица называется квадратной:
Матрица, у которой отличны от нуля только элементы, находящиеся на главной диагонали, называется диагональной:
Если у диагональной матрицы элементы равны 1, то матрица называется единичной и обозначается буквой Е:
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается буквой О
Треугольнойматрицей n-ого порядка называется квадратная матрица, все элементы которой, расположенные ниже главной диагонали, равны нулю
Действия над матрицами:
Суммой матрицы А и В называется такая матрица С, элементы которой равны сумме соответствующих элементов матриц А и В.
Складывать можно только матрицы, имеющие одинаковые число строк и столбцов.
Произведением матрицыА на число k называется такая матрица kA, каждый элемент которой равен kaij
Умножение матрицы А на матрицу В возможно только в том случае, если число столбцов первой матрицы равно числу строе второй матрицы.
|
2. Определители 2 и 3 порядков(вычисления, свойства)
определителем второго порядка называется число равное произведению элементов стоящих на главной диагонали минус произведение элементов стоящих на побочной диагонали.
Определителем третьего порядка называется число равное
и обозначаемое символом 
Свойства.
1) Транспонированный определитель равен данному.
2) Определитель, имеющий две одинаковые строки (столбца) равен нулю.
3) Постоянный множитель строки или столбца можно выносить за знак определителя.
4) Определитель, имеющий 2 пропорциональные строки или столбца равен 0.
5) Определитель, имеющий строку (столбец) состоящей из нулей равен 0.
6) Если в определителе поменять местами 2 соседние строки (столбца), то это равносильно умножению определителя на -1.
7) Величина определителя не изменится, если к элементам какой либо строки (столбца) прибавить элементы другой строки (столбца), умноженное на некоторое число.
8) Сумма произведений элементов какой либо строки или столбца на алгебраические дополнения другой строки или столбца равно 0.
|
3. Миноры и алгебраические дополнения
Минором M элемента элемента  служит определитель (n–1)-го порядка служит определитель (n–1)-го порядка , полученный из определителя п-го порядка , полученный из определителя п-го порядка вычеркиванием i-й строки и j-го столбца. вычеркиванием i-й строки и j-го столбца.
Алгебраическим дополнением A элемента элемента называют минор M называют минор M , взятый со знаком плюс или минус в зависимости от номеров вычеркиваемых строки и столбца, т. е. , взятый со знаком плюс или минус в зависимости от номеров вычеркиваемых строки и столбца, т. е.
A 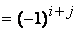 M M . .
|
5. Обратная матрица. Алгоритм вычисления
Матрица A−1 называется обратной по отношению к квадратной матрице A, если выполнено условие A−1⋅A=A⋅A−1=E, где E – единичная матрица, порядок которой равен порядку матрицы A. Невырожденная матрица – матрица, определитель которой не равен нулю. Соответственно, вырожденная матрица – та, у которой равен нулю определитель. Обратная матрица A−1 существует тогда и только тогда, когда матрица A – невырожденная. Если обратная матрица A−1 существует, то она единственная. Есть несколько способов нахождения обратной матрицы, и мы рассмотрим два из них. На этой странице будет рассмотрен метод присоединённой матрицы, который полагается стандартным в большинстве курсов высшей математики.
|
7. Системы линейных уравнений(основные понятия)
Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:

Решение системы уравнений — это последовательность чисел (k1, k2, ...,kn), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x1, x2, ..., xn дает верное числовое равенство.
решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:
1. Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.
Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.
2. Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.
|
8.Решение СЛУ методами Гаусса, Крамера, обратной матрицы
|
 Скачать 33.55 Kb.
Скачать 33.55 Kb.