|
|
Структурный анализ механизмов. 1 общие сведения
СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМОВ
1 ОБЩИЕ СВЕДЕНИЯ
Механизм – это система тел, предназначенная для преобразования движения одного или нескольких твердых тел в требуемое движение других твердых тел.
Твердое тело, входящее в состав механизма, называется звеном механизма. Под твердыми телами в теории механизмов и машин понимают как абсолютно твердые, так и деформируемые и гибкие тела.
В каждом механизме имеется неподвижное звено или звено, принимаемое за неподвижное (если механизм установлен на движущемся основании), которое называется стойкой. Из подвижных звеньев выделяют входные и выходные звенья. Входным звеном называется звено, которому сообщается движение, преобразуемое механизмом в требуемые движения других звеньев. Выходным звеном называется звено, совершающее движение, для выполнения которого предназначен механизм. Остальные звенья называются соединительными или промежуточными.
Подвижное соединение двух соприкасающихся звеньев называется кинематической парой. Совокупность поверхностей, линий и отдельных точек звена, по которым оно может соприкасаться с другим звеном, называется элементом кинематической пары. По характеру соприкосновения звеньев кинематические пары делят на низшие и высшие. Если соприкосновение звеньев происходит по поверхности, пара называется низшей, при соприкосновении по линии или в точке – высшей.
По числу наложенных условий связи 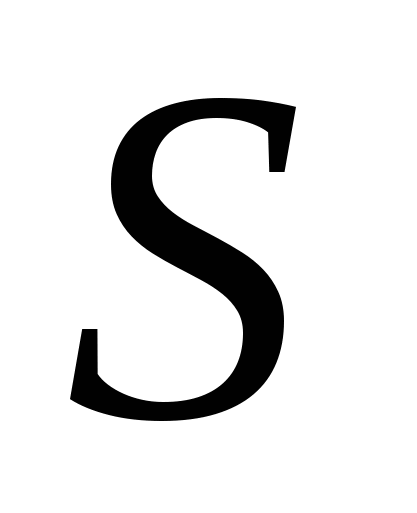 на относительные движения звеньев кинематические пары по предложению академика И.И. Артоболевского делят на классы. Для свободного тела в пространстве число степеней подвижности на относительные движения звеньев кинематические пары по предложению академика И.И. Артоболевского делят на классы. Для свободного тела в пространстве число степеней подвижности  равно шести, а равно шести, а 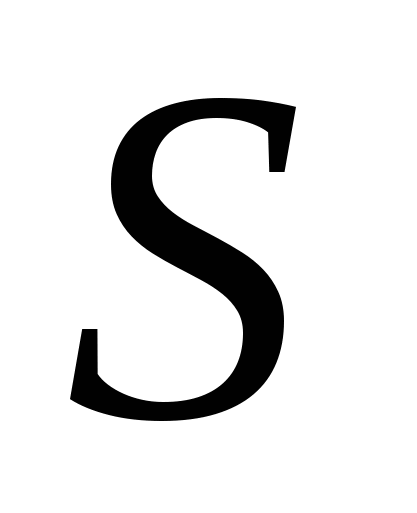 и и  связаны соотношением: связаны соотношением:  . При . При 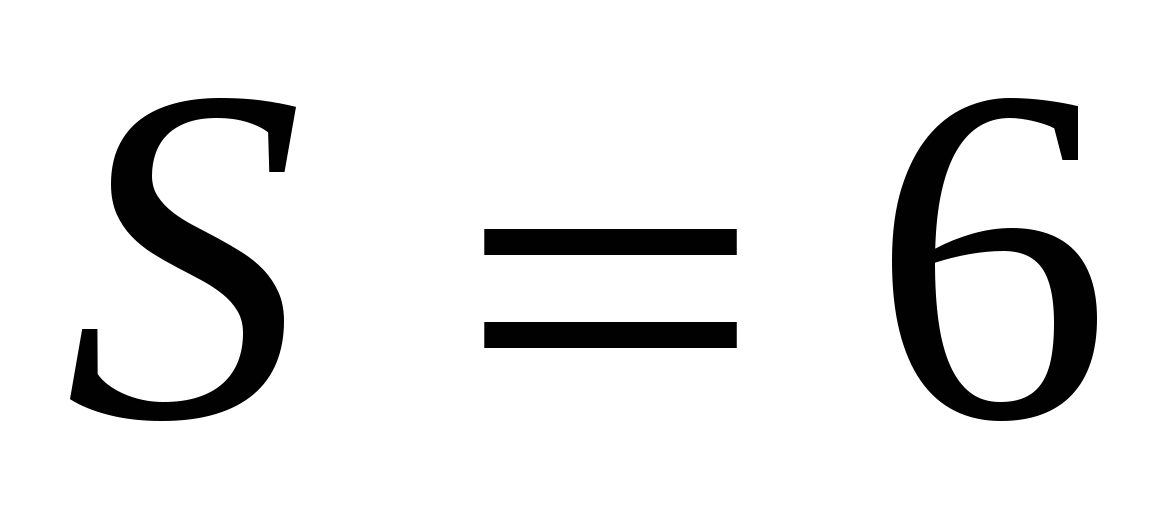 кинематическая пара становится жестким соединением (звеном), а при кинематическая пара становится жестким соединением (звеном), а при 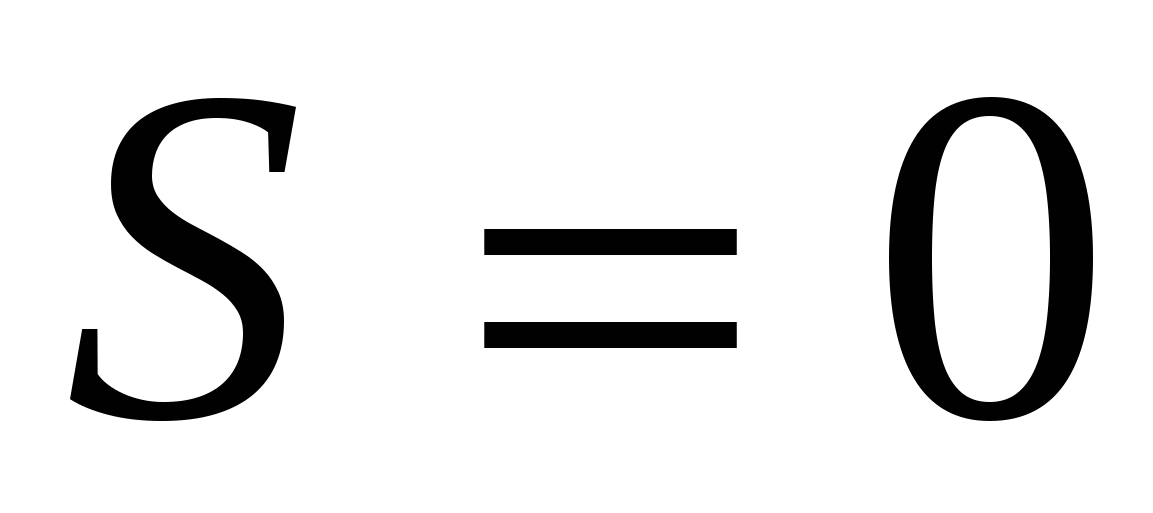 кинематической пары не существует, а два звена движутся независимо друг от друга в пространстве, то кинематической пары не существует, а два звена движутся независимо друг от друга в пространстве, то 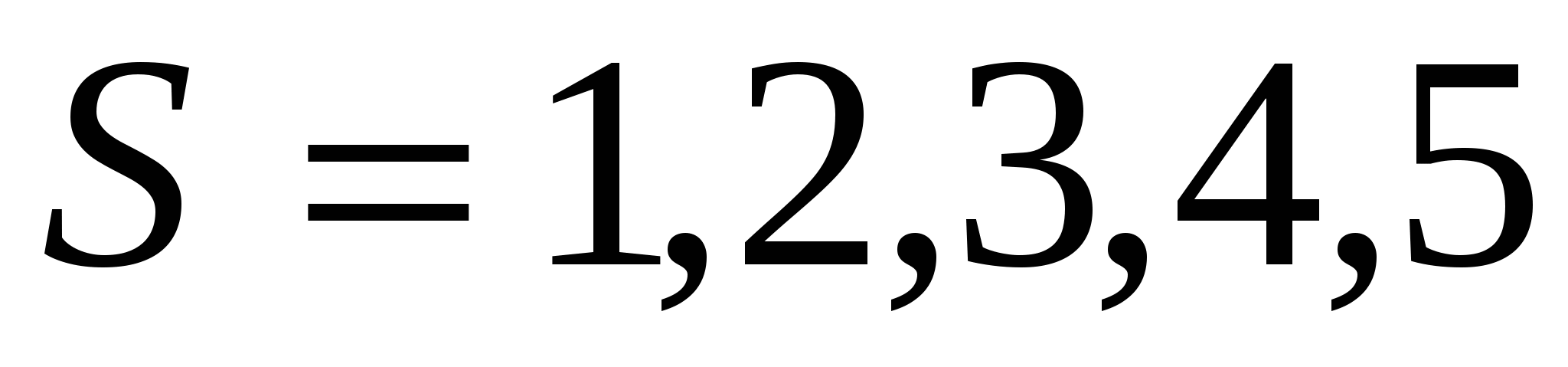 . .
Для структурного анализа используют структурную схему или кинематическую схему механизма. Для этого механизм изображают с помощью условных обозначений звеньев и кинематических пар по ГОСТ 2.770-68.
Формулы теории механизмов и машин, в которых связано число степеней свободы 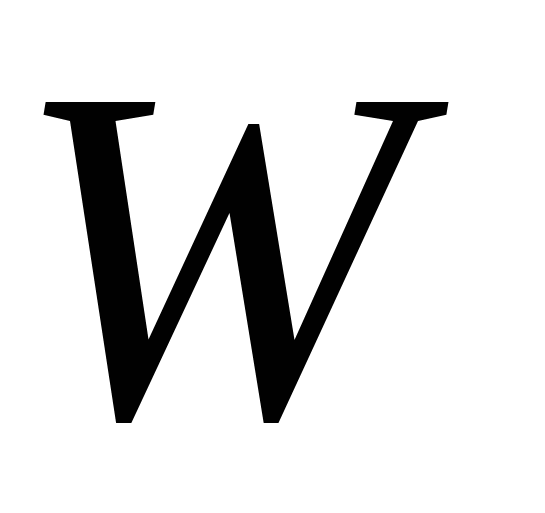 механизма с числом звеньев, числом и видом его подвижных соединений (кинематических пар), называют структурными. механизма с числом звеньев, числом и видом его подвижных соединений (кинематических пар), называют структурными.
Система, состоящая из  свободных звеньев, имеет в пространстве свободных звеньев, имеет в пространстве 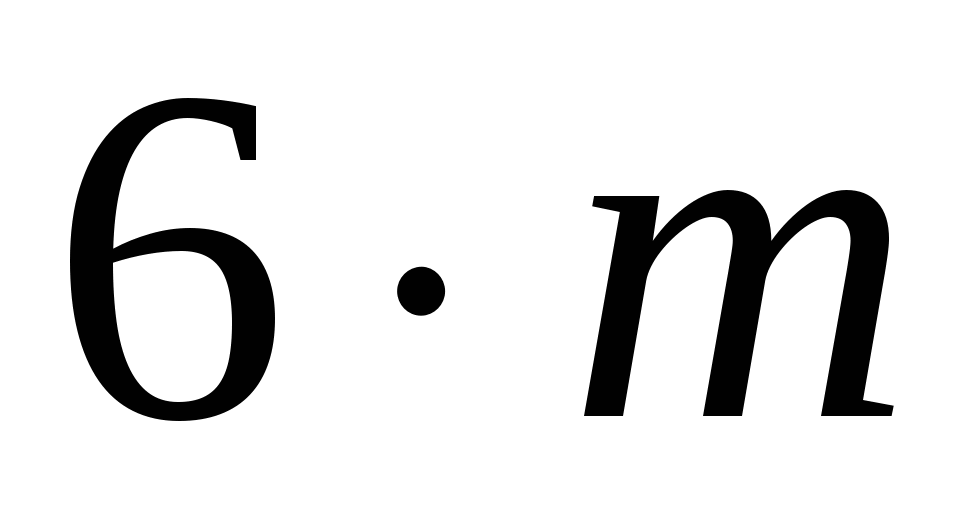 степеней свободы. Если соединить эти звенья кинематическими парами, их относительное движение ограничивается наложенными условиями связи степеней свободы. Если соединить эти звенья кинематическими парами, их относительное движение ограничивается наложенными условиями связи 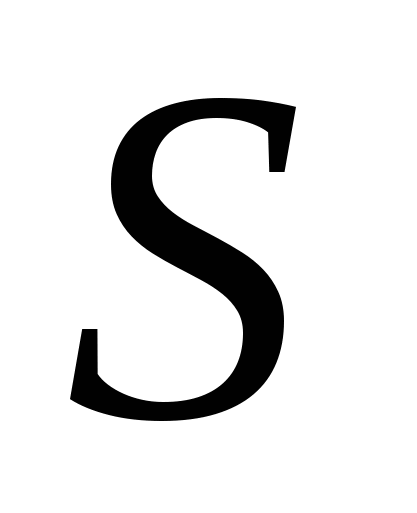 . Если число пар каждого класса обозначить через . Если число пар каждого класса обозначить через 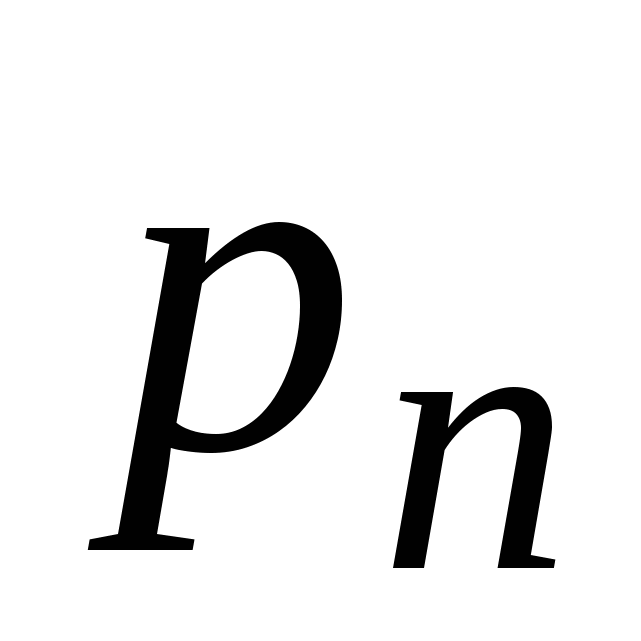 , где индекс , где индекс  - номер ее класса, то в общем случае в кинематической цепи будет - номер ее класса, то в общем случае в кинематической цепи будет 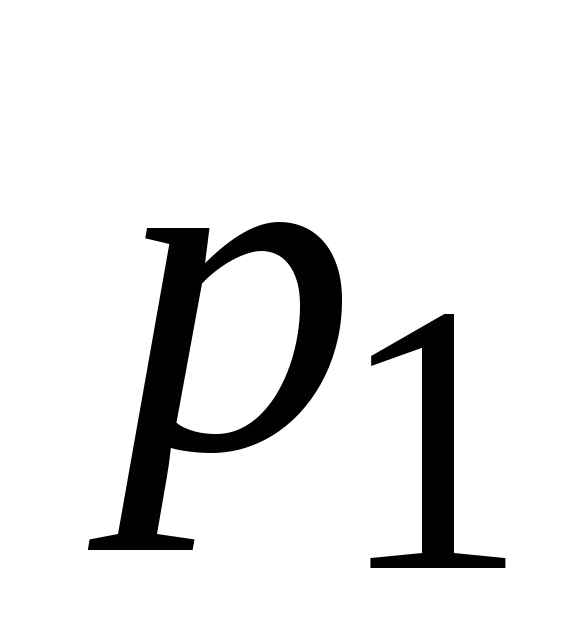 пар первого класса, пар первого класса, 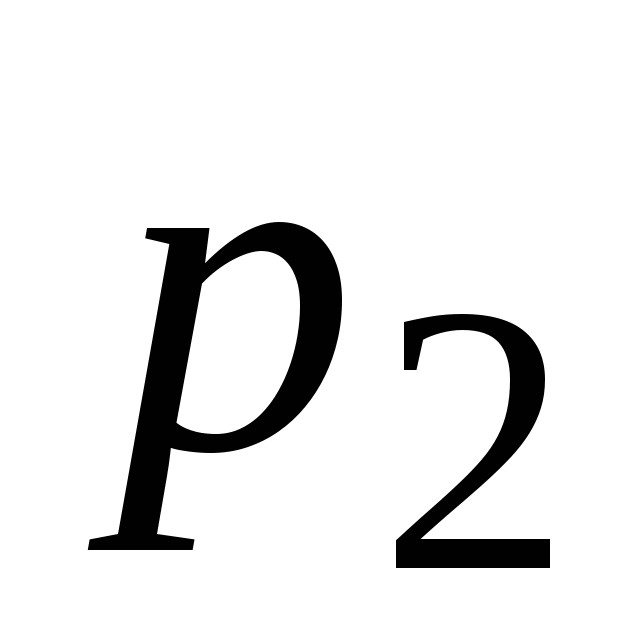 пар второго класса и т.д. Следовательно, из пар второго класса и т.д. Следовательно, из 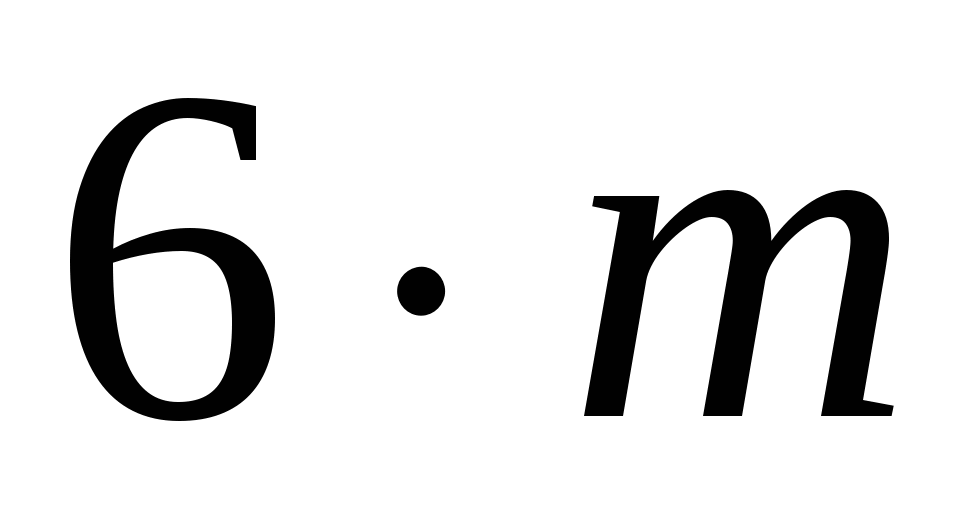 степеней подвижности, которые ограничиваются кинематическими парами. Тогда степеней подвижности, которые ограничиваются кинематическими парами. Тогда
число степеней свободы пространственных механизмов определится по формуле [1]:
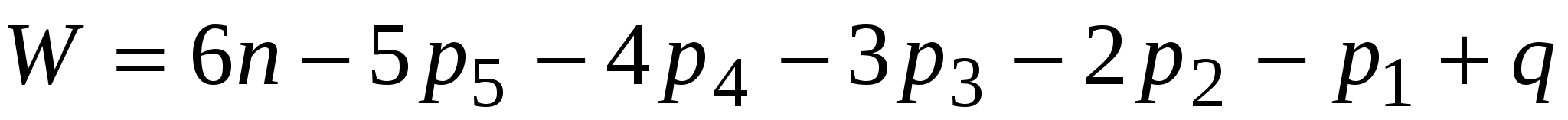 , (1) , (1)
где  - число подвижных звеньев, равное - число подвижных звеньев, равное  ; ;  - общее число звеньев (со стойкой); - общее число звеньев (со стойкой); 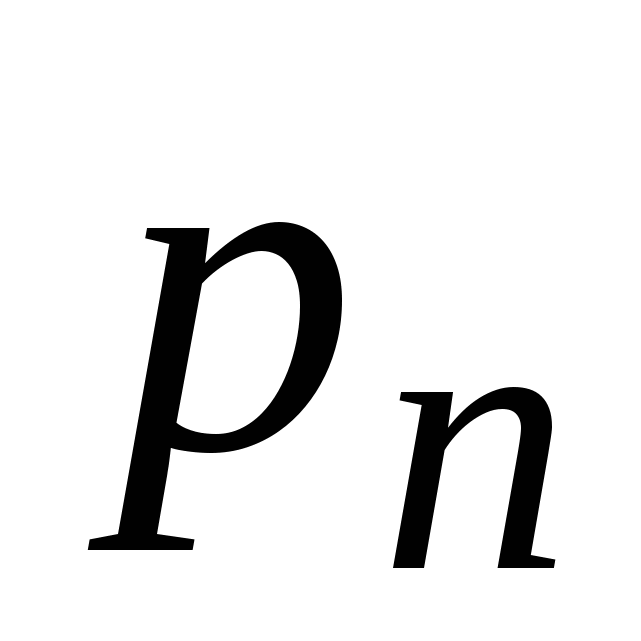 - число кинематических пар соответствующего класса; - число кинематических пар соответствующего класса; 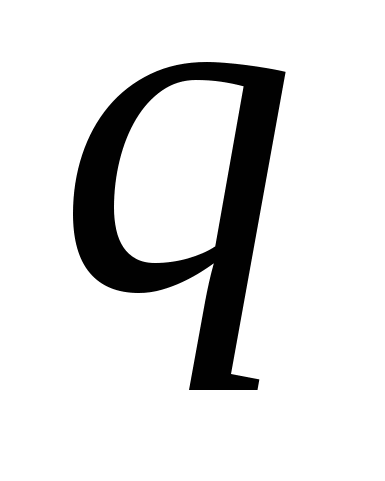 - избыточные (пассивные) связи, устранение которых не увеличивает подвижности механизма. - избыточные (пассивные) связи, устранение которых не увеличивает подвижности механизма.
Наличие избыточных связей в механизме повышает требования к точности изготовления звеньев механизма.
Приняв 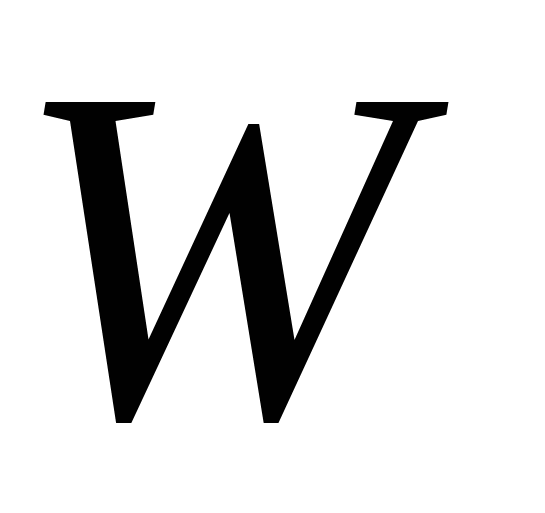 , равным числу обобщенных координат механизма, найденных из геометрических соображений, из формулы (1.) можно найти число избыточных связей: , равным числу обобщенных координат механизма, найденных из геометрических соображений, из формулы (1.) можно найти число избыточных связей:
 . (2) . (2)
Если 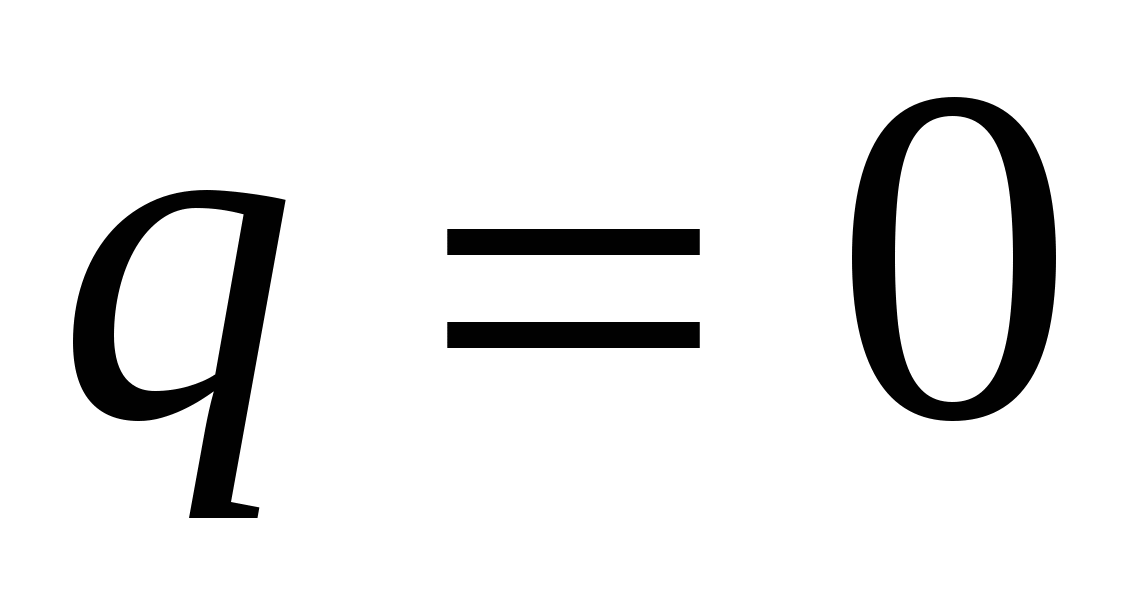 , то в механизме избыточных связей нет, и требования к точности изготовления звеньев механизма значительно снижаются. , то в механизме избыточных связей нет, и требования к точности изготовления звеньев механизма значительно снижаются.
Число степеней свободы плоских механизмов рассчитывают по формуле, предложенной П.Л. Чебышевым в 1869 г.:
 . (3) . (3)
При известном 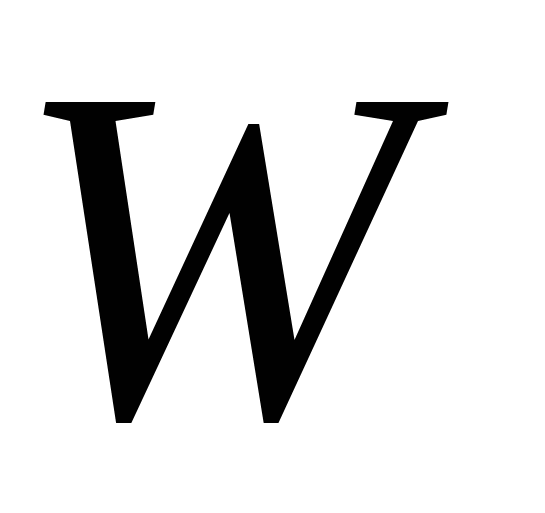
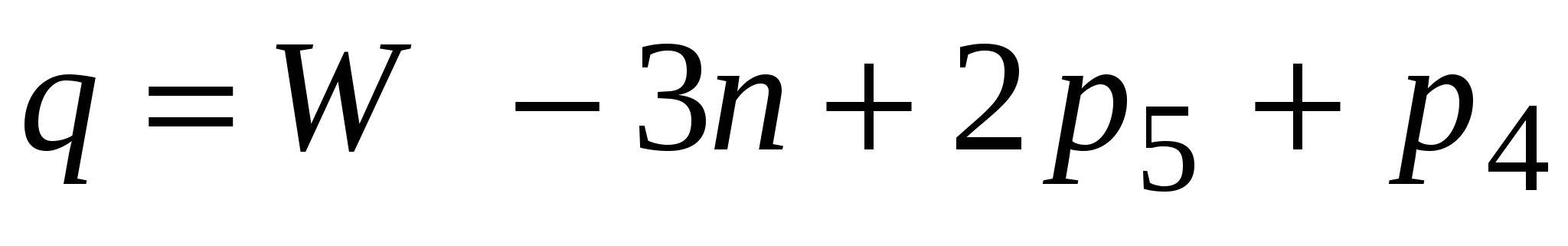 . (4) . (4)
Если плоский механизм изготовлен точно, расчет можно выполнять по формуле (3). При наличии погрешностей изготовления звенья механизма двигаются в разных плоскостях. В этом случае число степеней свободы определяют по формуле (1). При этом число степеней свободы механизма равно числу входных звеньев.
Рассмотрим в качестве примера плоский кривошипно-ползунный механизм (рисунок 1а). Для этого механизма при 
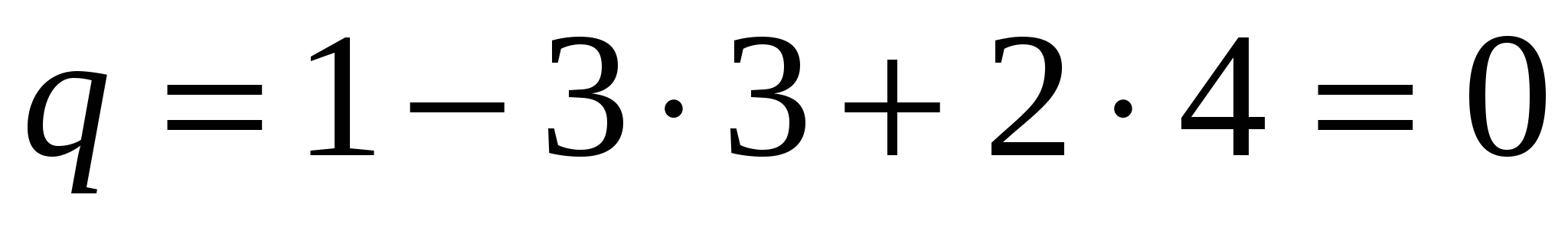 , ,
т.е. избыточных связей нет.
 а) б) в) а) б) в)
Рисунок 1 – Кинематические схемы кривошипно-ползунного механизма.
Если же механизм изготовлен с погрешностями и звенья двигаются не в одной, а в разных плоскостях, его необходимо рассматривать как пространственный (рисунок 1б). Для такого механизма при 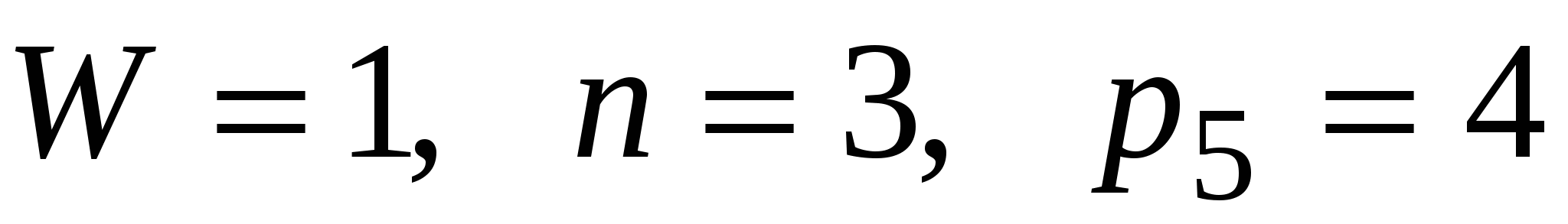
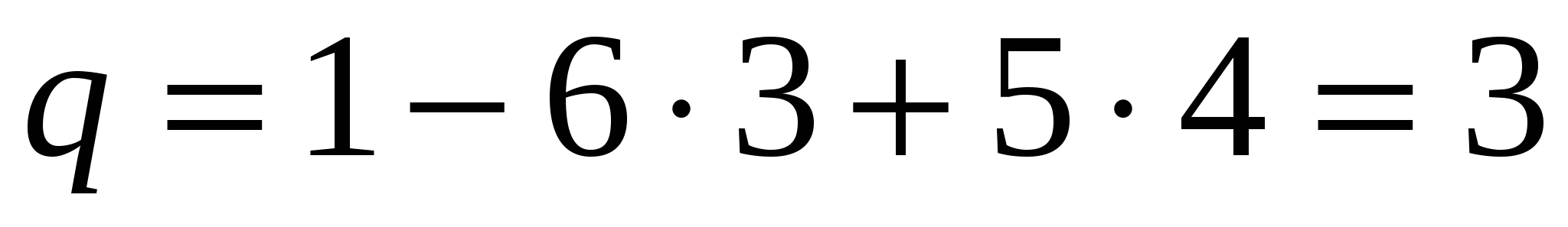 . .
Следовательно, четыре кинематических пары 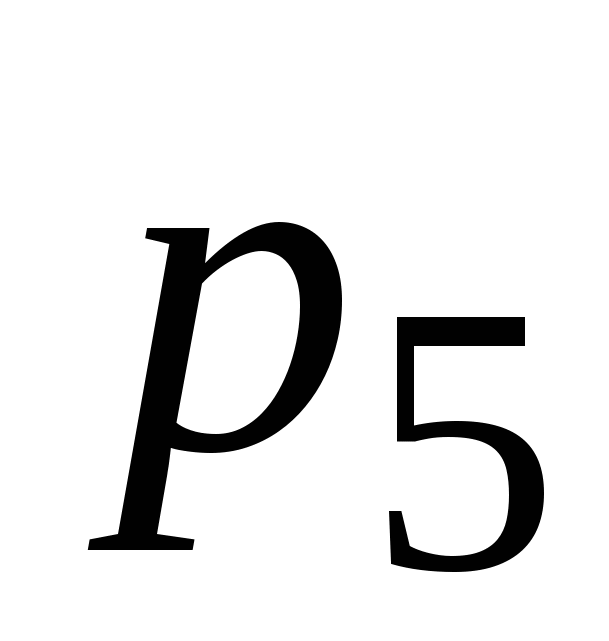 в пространственном механизме использовать нежелательно. Вместо двух пар в пространственном механизме использовать нежелательно. Вместо двух пар 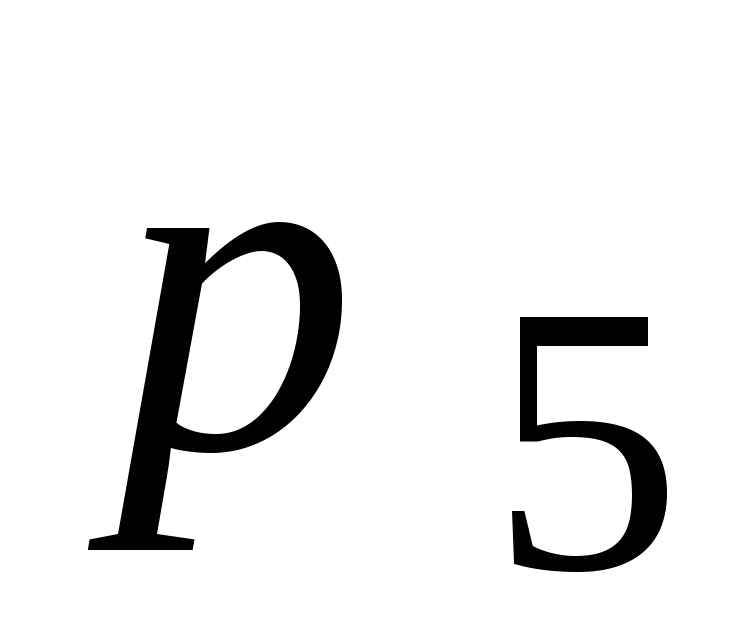 можно применить пару можно применить пару 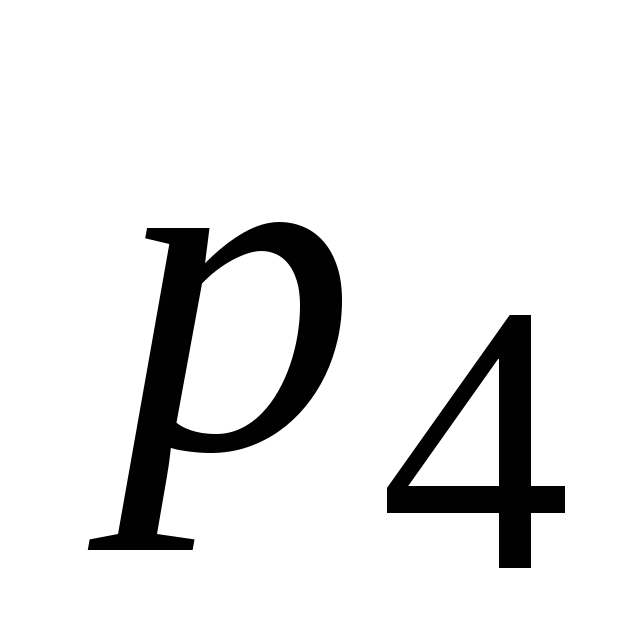 и и  (рисунок 1в). Тогда (рисунок 1в). Тогда
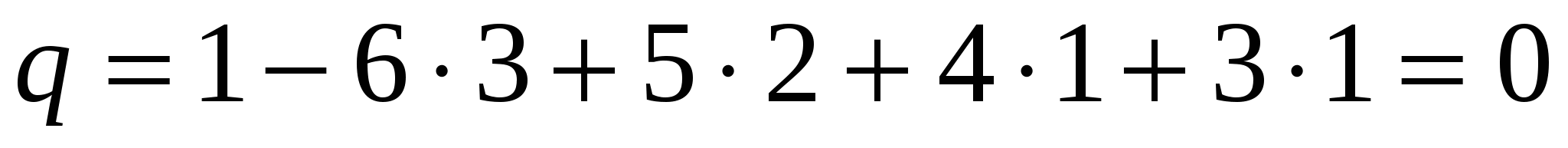 . .
В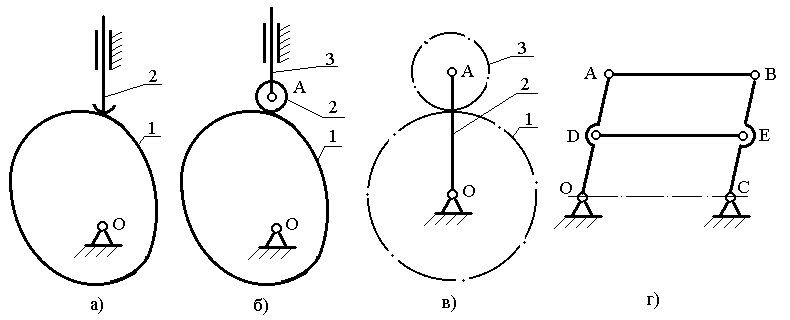 ыполним структурный анализ плоского механизма, в составе которого наряду с низшими парами имеется высшая пара. Для этого рассмотрим кулачковый механизм с поступательно движущимся толкателем (рисунок 2а). ыполним структурный анализ плоского механизма, в составе которого наряду с низшими парами имеется высшая пара. Для этого рассмотрим кулачковый механизм с поступательно движущимся толкателем (рисунок 2а).
Рисунок 2 – Кинематические схемы механизмов.
Число степеней свободы механизма определим по формуле (3). Для этого механизма  Высшая пара образована в месте соприкосновения звеньев 1 и 2. При заданном движении входного звена 1 (кулачка) выходное звено 2 (толкатель) совершает вполне определенное движение. Высшая пара образована в месте соприкосновения звеньев 1 и 2. При заданном движении входного звена 1 (кулачка) выходное звено 2 (толкатель) совершает вполне определенное движение.
Другой пример механизма с высшей парой – дифференциальный зубчатый механизм (рисунок 2в), в котором  (в месте зацепления зубчатых колес). Избыточных связей в этом механизме нет, то есть (в месте зацепления зубчатых колес). Избыточных связей в этом механизме нет, то есть 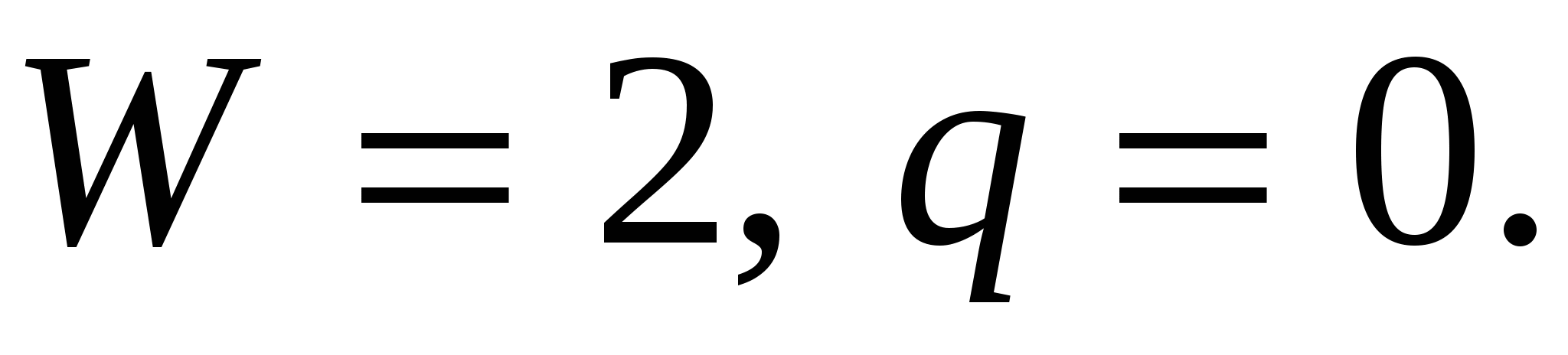 Для осуществления движения выходного звена 3 необходимо иметь два входных звена. Такими звеньями могут быть солнечное колесо 1 и водило 2. Для осуществления движения выходного звена 3 необходимо иметь два входных звена. Такими звеньями могут быть солнечное колесо 1 и водило 2.
Необходимо иметь в виду, что в механизмах, используемых в технике, кроме степеней свободы и связей, активно воздействующих на характер движения, могут встречаться степени свободы и условия связи, не влияющие на характер движения механизма в целом и на закон движения выходного звена. Эти связи называют избыточными, или пассивными, а степени свободы – лишними; их не следует учитывать при определении числа степеней свободы механизма.
Рассмотрим схему (рисунок 2г), используемую в механизмах грохотов, в приводе колес электроприводов для повышения жесткости системы и равномерного распределения нагрузки. В этом механизме, называемом механизмом параллельных кривошипов с дополнительным шатуном  , должно быть , должно быть 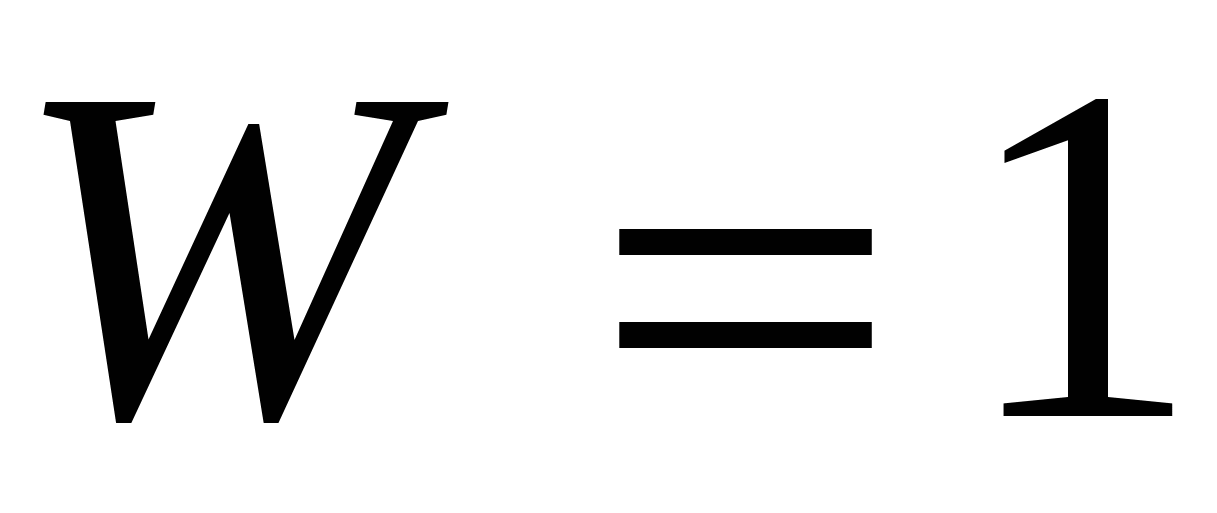 , так как при заданном движении входного звена выходное звено , так как при заданном движении входного звена выходное звено  движется совершенно определенно; движется совершенно определенно; 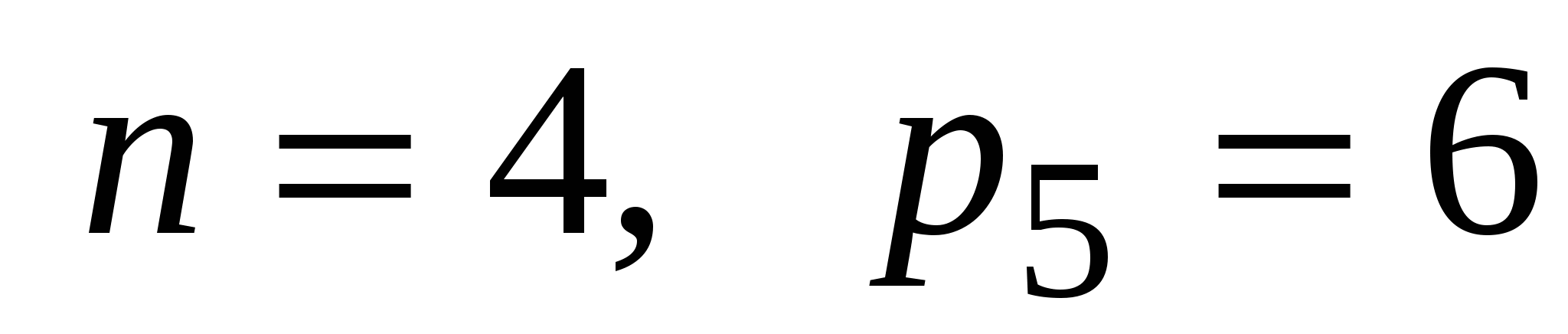 и и
 , ,
т.е. механизм имеет одну избыточную связь. Однако при выполнении соотношений для длин звеньев 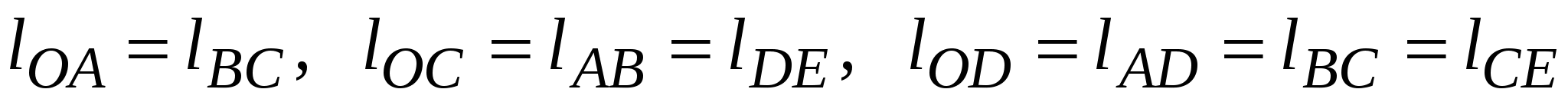 наличие звена наличие звена  не изменит движения шарнирного четырехзвенника не изменит движения шарнирного четырехзвенника 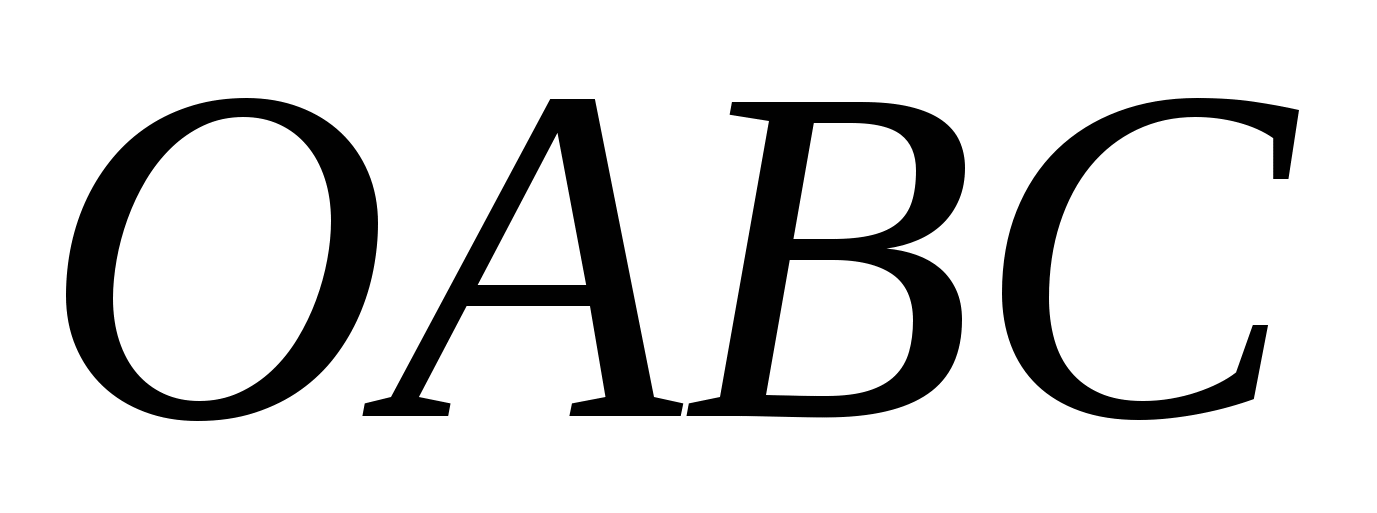 , имеющего , имеющего 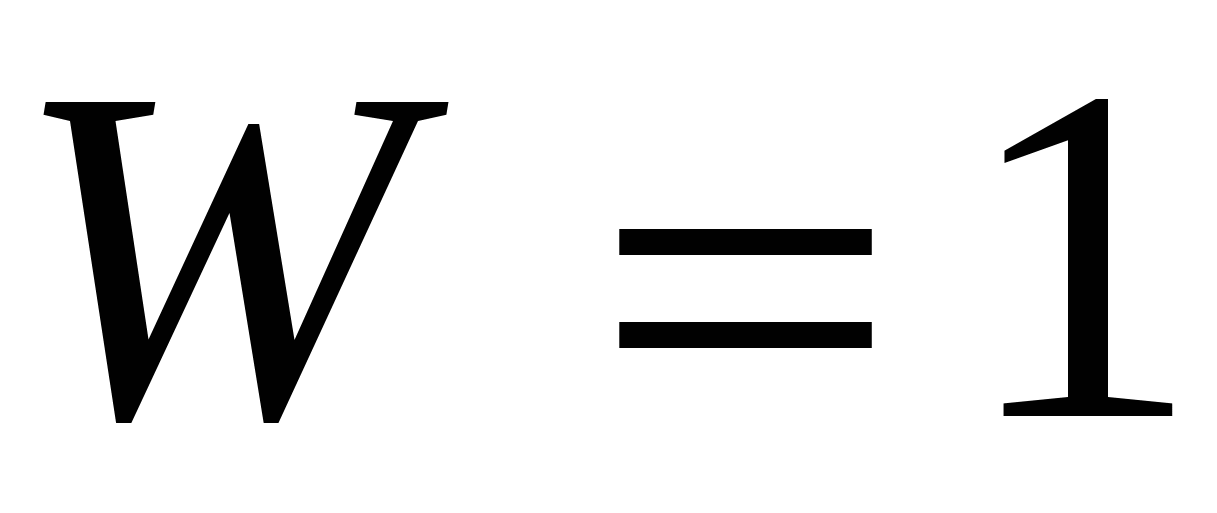 и и 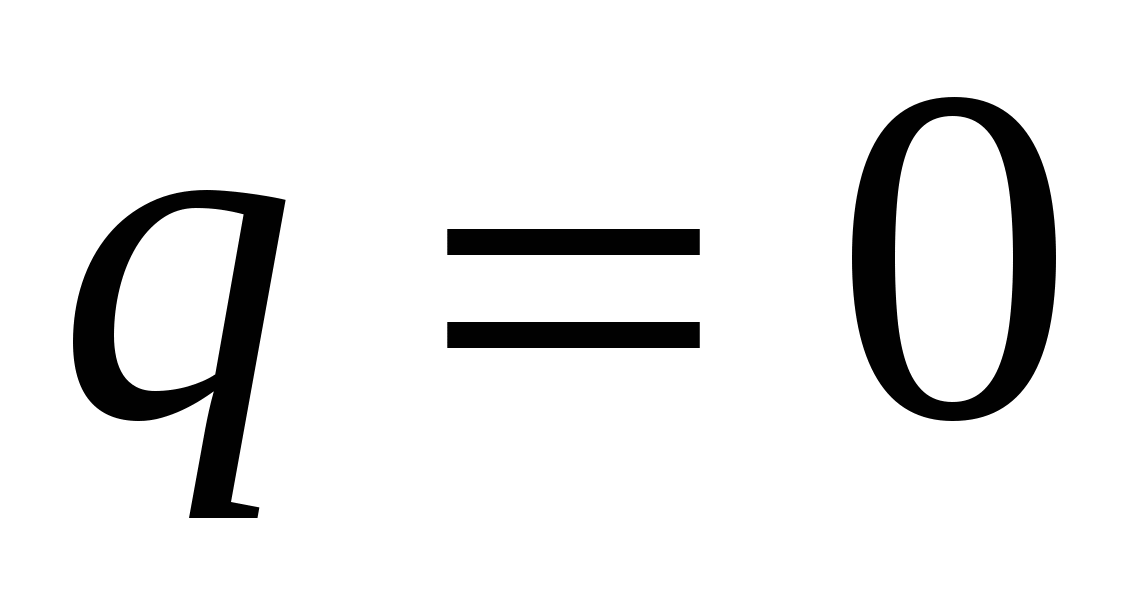 . Если из схемы удалить это звено, относительное движение остальных звеньев сохранится прежним, поэтому связь . Если из схемы удалить это звено, относительное движение остальных звеньев сохранится прежним, поэтому связь  называют избыточной. называют избыточной.
Рассмотрим кулачковый механизм с поступательно движущимся толкателем 3. Толкатель в месте соприкосновения с кулачком 1 снабжен роликом 2 (рисунок 2б). У этого механизма избыточная связь отсутствует, то есть 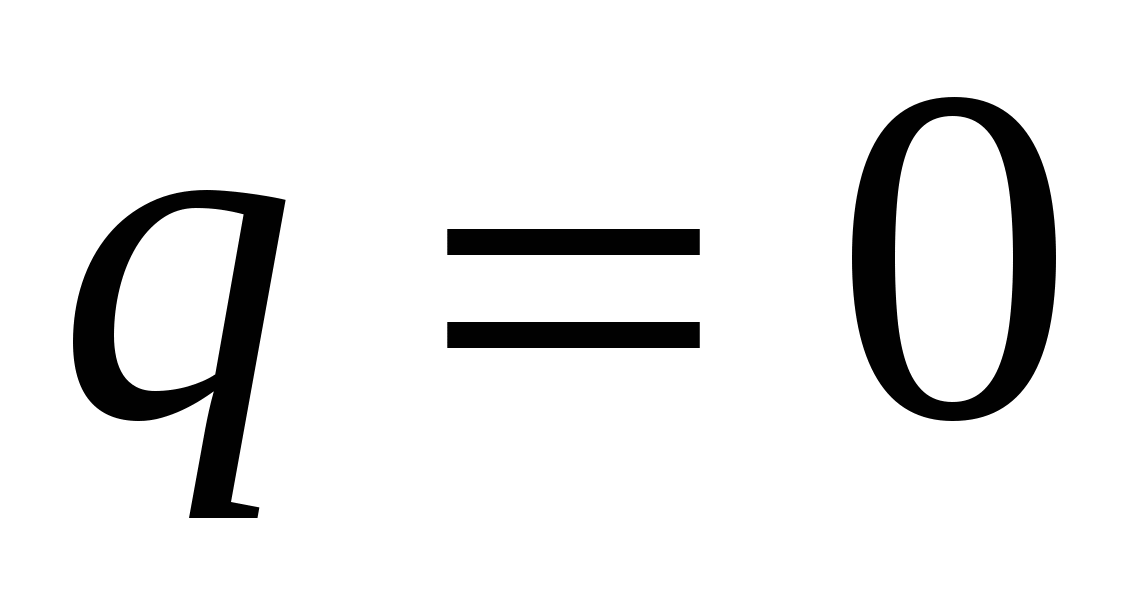 ; при этом ; при этом 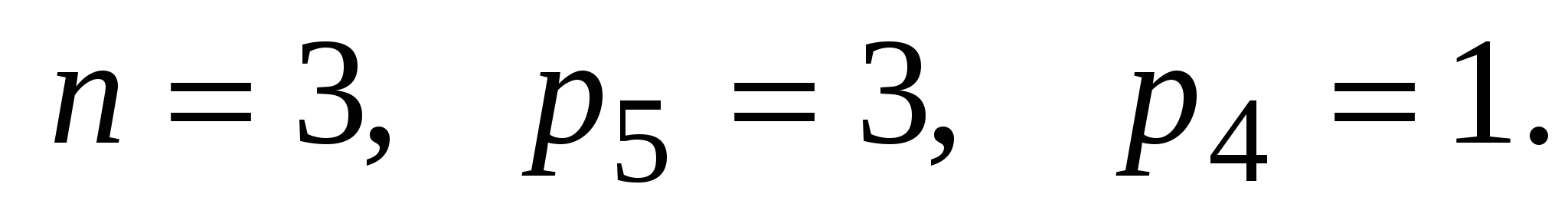 Следовательно, Следовательно,
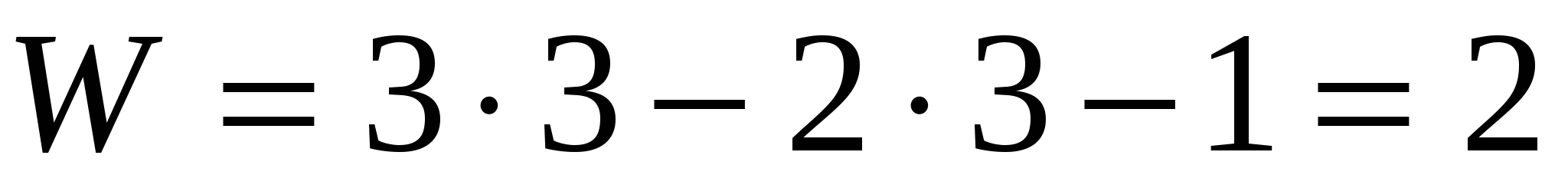 . .
При определенном движении входного звена (кулачка) выходное звено (толкатель) движется также вполне определенно. Для этого механизма должно быть 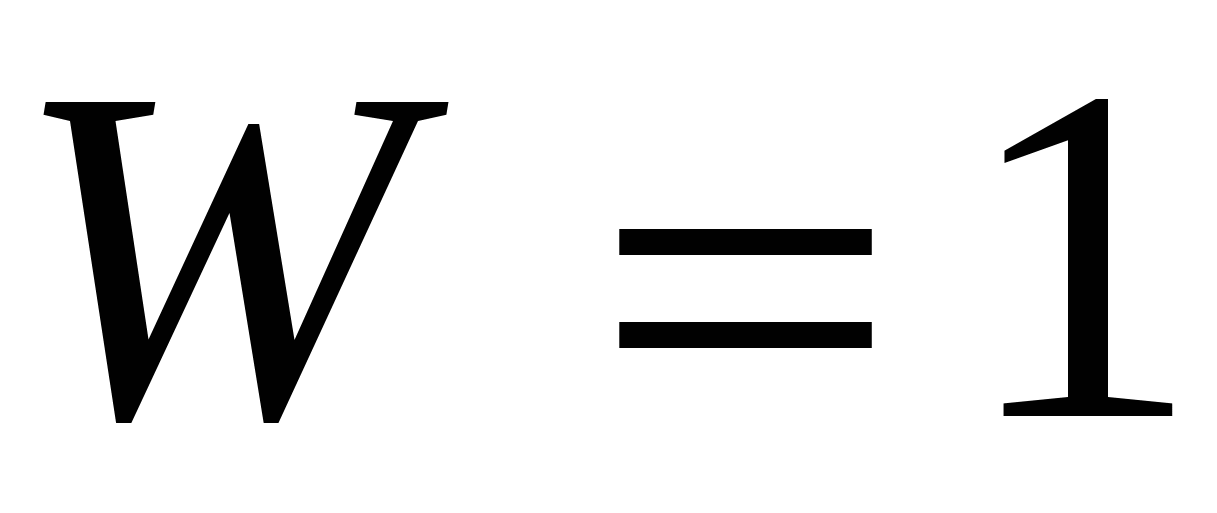 , поэтому ролик можно удалить и вместо механизма, изображенного на рисунке 2б, использовать механизм, который показан на рисунке 2а. Свободно поворачивающийся ролик дает лишнюю степень свободы. Его устанавливают для уменьшения трения между кулачком и толкателем, так как в этом случае трение скольжения заменяется трением качения. , поэтому ролик можно удалить и вместо механизма, изображенного на рисунке 2б, использовать механизм, который показан на рисунке 2а. Свободно поворачивающийся ролик дает лишнюю степень свободы. Его устанавливают для уменьшения трения между кулачком и толкателем, так как в этом случае трение скольжения заменяется трением качения.
При структурном анализе зазоры в кинематических парах не учитывают.
В действительности при наличии зазоров подвижность кинематической пары повышается и влияние избыточных связей несколько уменьшается.
2 ПРИНЦИП ОБРАЗОВАНИЯ МЕХАНИЗМОВ
Механизм состоит из входного звена с одной степенью свободы и присоединяемых к нему и стойке кинематических цепей (структурных групп) с нулевой степенью подвижности относительно тех звеньев, к которым группа присоединяется. Структурную группу с нулевой степенью подвижности называются группой Л.В. Ассура, предложившего метод образования механизмов.
Входное звено, соединенное со стойкой, называют начальным механизмом или механизмом первого класса (рисунок 3а).
Для групп Ассура
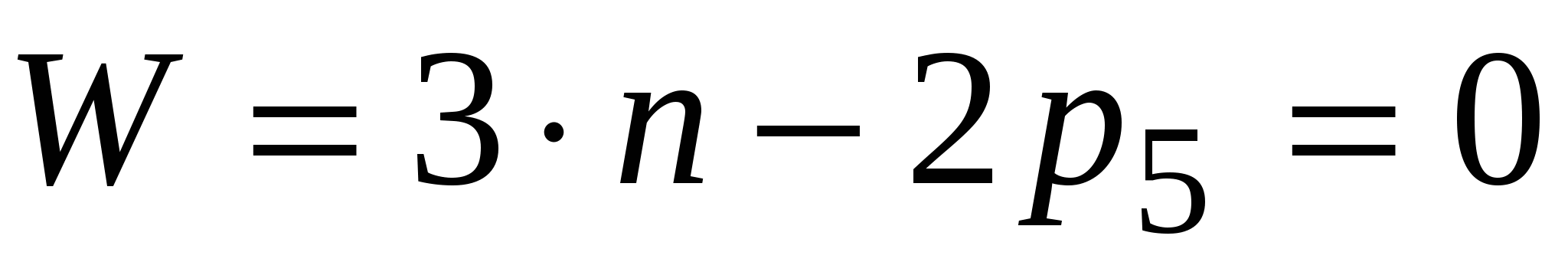 . (5) . (5)
Следовательно, присоединение группы Ассура к любому звену не меняет степени свободы всего механизма. В механизме может быть несколько групп Ассура, причем они могут присоединяться непосредственно к начальному звену и стойке, последовательно к предыдущей группе и стойке или последующей группе.
Число звеньев  и число низших кинематических пар и число низших кинематических пар 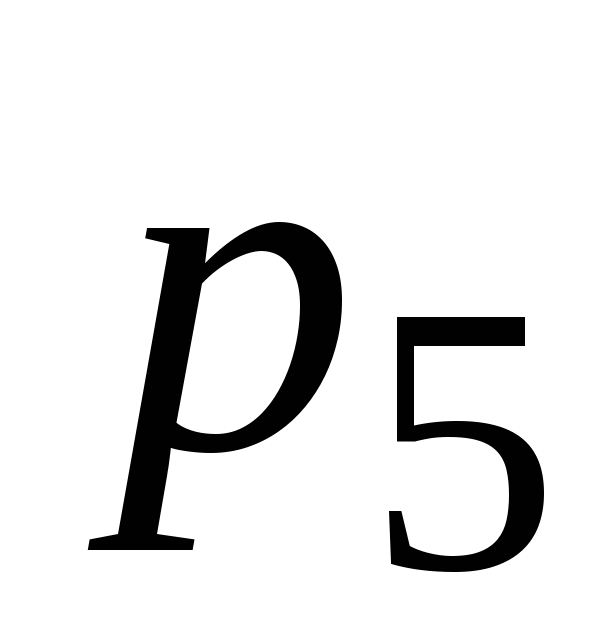 могут быть только целыми, причем могут быть только целыми, причем
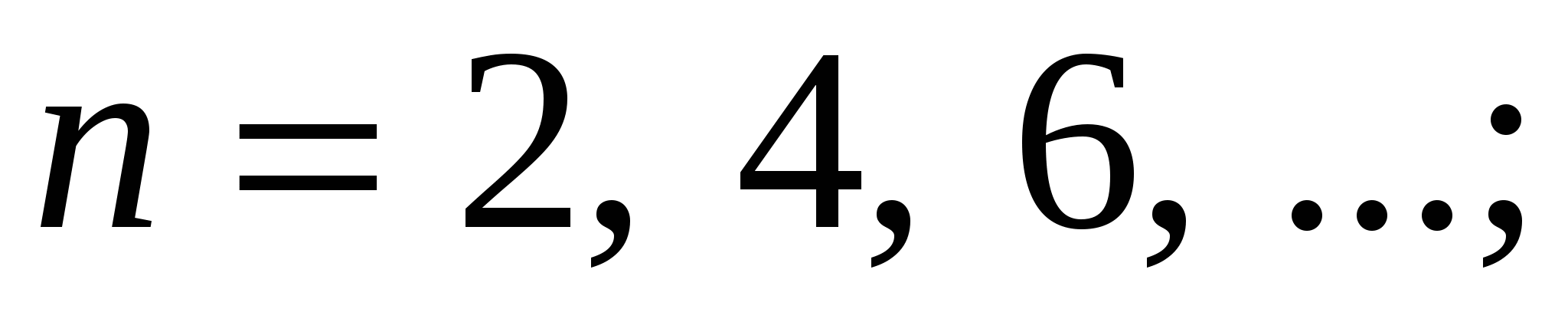 
Структурную группу, состоящую из двух подвижных звеньев и трех низших кинематических пар, называют двухповодковой (рисунок 3б) или
а ) б) в) г) ) б) в) г)
Рисунок 3 – Схемы к определению класса группы Ассура.
группой Ассура второго класса. Класс группы определяется классом наивысшего по классу контура, входящего в его состав. Класс контура определяется количеством кинематических пар, в которые входят образующие его звенья (рисунок 3в,г). На рисунке 3в приведена трехповодковая или группа Ассура третьего класса. На рисунке 3г приведена группа Ассура четвертого класса.
На рисунке 4 изображена схема механизма с 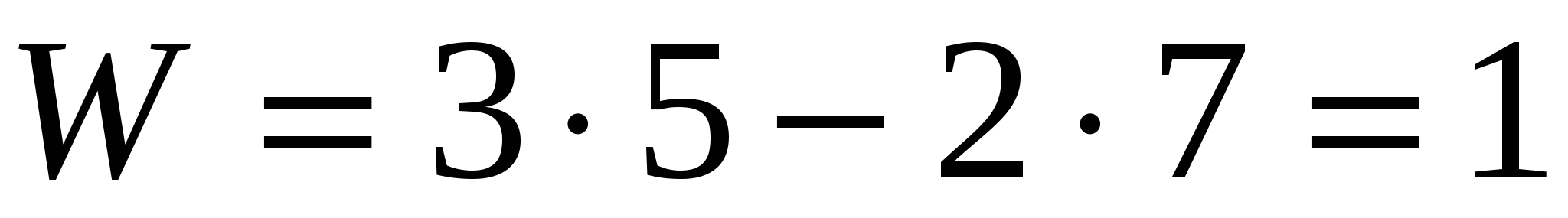 , состоящего из входного звена с , состоящего из входного звена с 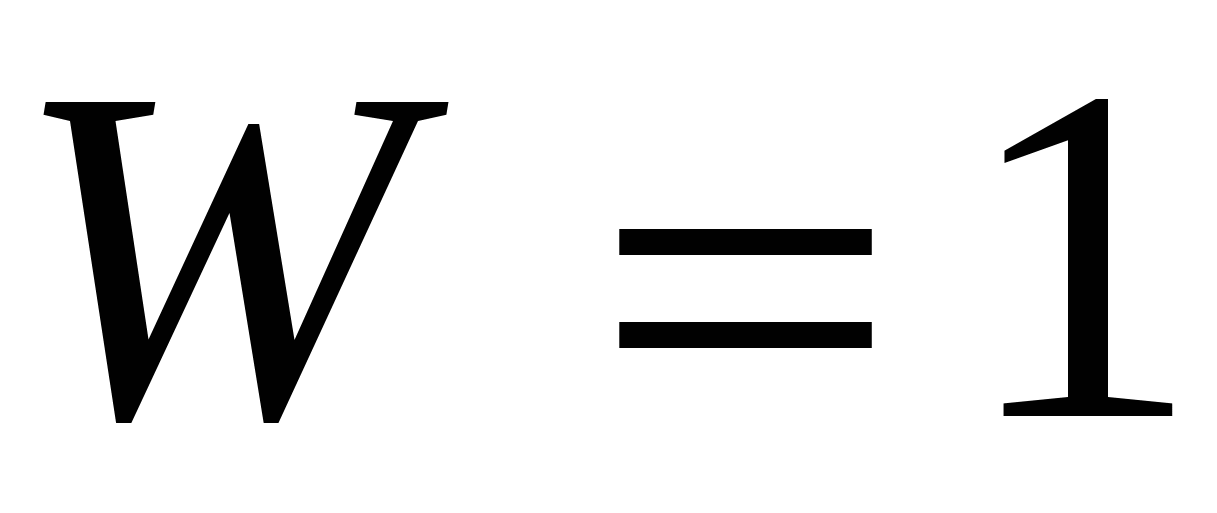 и двух двухповодковых групп с и двух двухповодковых групп с 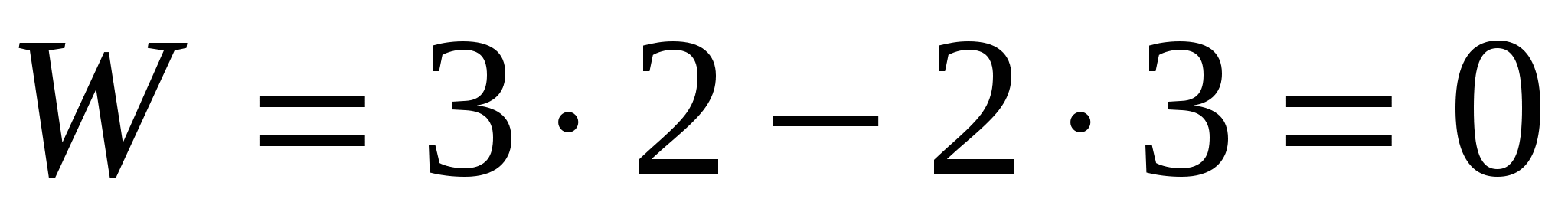 . .
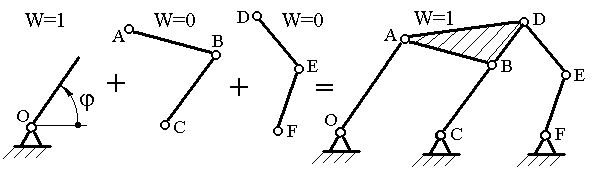
Рисунок 4 – Пример образования плоского шестизвенного механизма.
На рисунке 5приведена схема механизма с 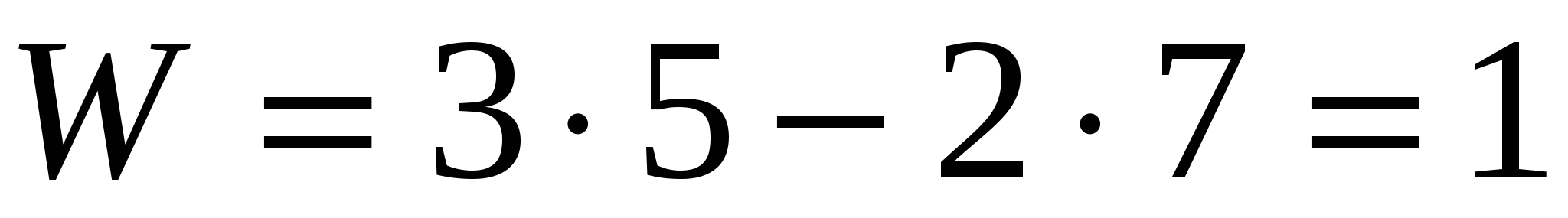 , образованного из входного звена с , образованного из входного звена с 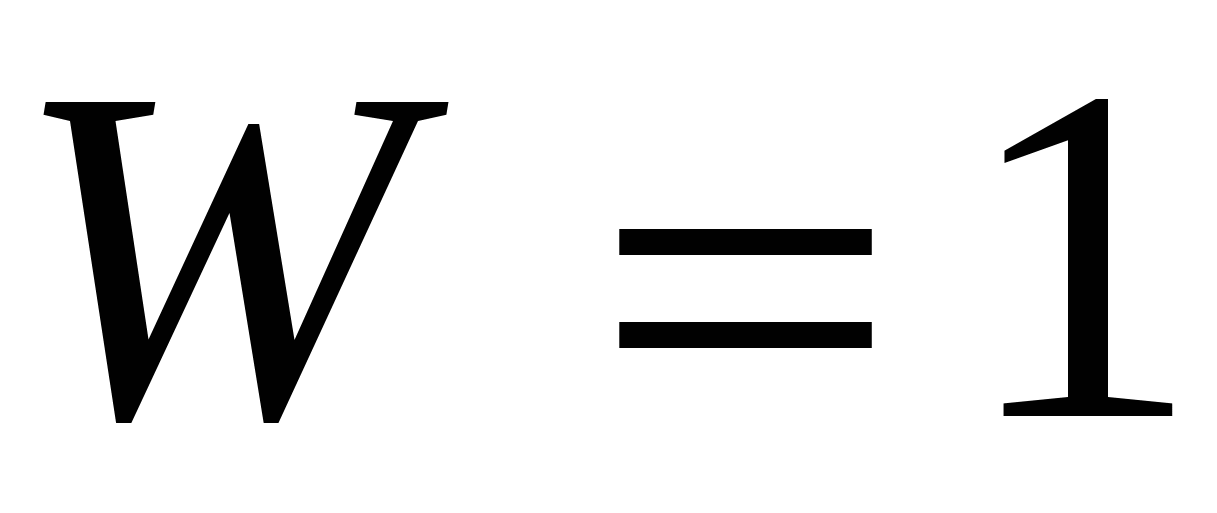 и одной группы третьего класса с и одной группы третьего класса с  . .
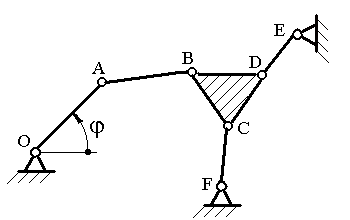
Рисунок 5 – Кинематическая схема механизма третьего класса. Порядок выполнения работы
1. Изобразить кинематические схемы предложенных механизмов согласно ГОСТ 2.770-68.
2. Рассчитать число степеней свободы механизмов и число избыточных связей по формулам (1), (2) для пространственных механизмов и по формулам (3), (4) для плоских механизмов.
3. Разбить рычажный механизм на входное звено и группы Ассура с нулевой степенью подвижности. Начертить это звено и группы Ассура отдельно. Провести структурный анализ групп Ассура.
КОНТРОЛЬНЫЕ ВОПРОСЫ
По какому признаку классифицируются кинематические пары?
Как определить число степеней свободы механизма?
Чем различаются расчеты числа степеней свободы плоского и пространственного механизма?
Что такое группа Ассура и какова ее роль в расчетах по ТММ?
|
|
|
 Скачать 182 Kb.
Скачать 182 Kb.
 а) б) в)
а) б) в)  ыполним структурный анализ плоского механизма, в составе которого наряду с низшими парами имеется высшая пара. Для этого рассмотрим кулачковый механизм с поступательно движущимся толкателем (рисунок 2а).
ыполним структурный анализ плоского механизма, в составе которого наряду с низшими парами имеется высшая пара. Для этого рассмотрим кулачковый механизм с поступательно движущимся толкателем (рисунок 2а). ) б) в) г)
) б) в) г)
